Subsections

• 9.2.1 Capacitance Analysis
• 9.2.2 Resistance Analysis
• 9.2.3 Finite Element Solution Procedure
• 9.2.4 Transformation into GSSE 

9.2 Basic Equations and Discretization

Maxwell's equations, given in Section 1.2, are the basic equations for the examples given here. For the stationary electrostatical case, the time derivatives vanish and $\mathrm{curl} \left( \ensuremath{\mathbf{E}} \right) = 0$ is obtained. Such an equation can be expressed by a scalar potential $\ensuremath{\mathbf{E}} = - \mathrm{grad} \left( {\ensuremath{\varphi}} \right)$ which is subsequently used to derive the capacitance and resistance analysis [114].

9.2.1 Capacitance Analysis

For the given stationary case with linear dielectric, the ratio of charge $Q$ and voltage $U$ of conductors is constant and is called capacitance $C = \frac{Q}{U}$ . Due to the fact that the inner part of the conductors is free of electric field, the charge is distributed only on their surfaces. The charge distribution is derived from $\ensuremath{\mathbf{D}}$ by means of a surface charge $\sigma$ as given in Section 1.2 and Equation 1.13. By integration of the charge on the surface of the conductor ${\ensuremath{\Gamma}}_i$ the following is obtained:

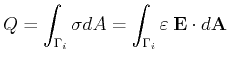$$Q = \int_{{\ensuremath{\Gamma}}_i} \sigma dA = \int_{{\ensuremath{\Gamma}}_i} \varepsilon \ensuremath{\mathbf{E}} \cdot d\ensuremath{\mathbf{A}}$$ (9.1)

Then the capacitance $C$ can be derived. Another way can be described by the energy method, where the stored energy is given by $W =\frac{C U^2}{2}$ expressed in local field terms:

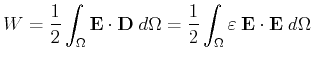$$W = \frac{1}{2} \int_{{\ensuremath{\Omega}}} \ensuremath{\mathbf{... ...n \ensuremath{\mathbf{E}} \cdot \ensuremath{\mathbf{E}} d{\ensuremath{\Omega}}$$ (9.2)

Here, the calculation domain covers the complete dielectric part and expands, theoretically, into infinite space. Therefore it is important to emphasize that most of the field energy is contained near the conductors, and so only a small part of the integration domain has to be covered [114].

Both of these calculation mechanisms require the calculation of the electric field $\ensuremath{\mathbf{E}}$ , where the charge integration requires only the field at the surface of the conductor, which can be expressed by a scalar potential ${\ensuremath{\varphi}}$ . The Maxwell equation $\mathrm{div} \left( \ensuremath{\mathbf{D}} \right) = \varrho$ , and the fact that an isolator does not carry electric charge ( $\varrho = 0$ ), the following equations are used to determine a potential distribution as well as for the extraction of the capacity of a given domain:

$$\mathrm{div} \left( \varepsilon\; \mathrm{grad} \left( {\ensuremath{\varphi}} \right) \right) = 0 \quad \textnormal{on} \; {\ensuremath{\Omega}}$$ (9.3)

$$\ensuremath{\mathbf{n}} \cdot \varepsilon \mathrm{grad} \left( {\ensuremath{\varphi}} \right) = 0 \quad \textnormal{on} \; {\ensuremath{\Gamma}}$$ (9.4)

$${\ensuremath{\varphi}} = {\ensuremath{\varphi}}_k \quad \textnormal{on} \; {\ensuremath{\Gamma}}_{c,k}$$ (9.5)

where ${\ensuremath{\Omega}}$ is a bounded open domain with boundary ${\ensuremath{\Gamma}}$ , and conductor boundaries ${\ensuremath{\Gamma}}_{c,k}$ , and ${\ensuremath{\varphi}}_k$ represent conductor surface potentials .

As introduced in Section 2.3, the finite element formulation is represented by the following equation system for $N$ -elements:

$$\sum_{j=1}^{N} {\ensuremath{\varphi}}_j \int_{\ensuremath{\tau_{3... ...{3}^{i}}} {\ensuremath{\phi}}_p {\ensuremath{\phi}}_q  d{\ensuremath{\Gamma}}$$ (9.6)

where the following expression for the charge distribution is used $\sigma = \sum_{j=1}^N {\ensuremath{\phi}}_{q,j} \sigma_j$ . This problem is linear and the global system matrix is simply obtained by assembling $\Pi$ with the corresponding node index transformation into the global matrix.

9.2.2 Resistance Analysis

The electric resistance can be described by the global law $R=\frac{U}{I}$ . The resistance of a conductor can then be calculated by using a potential on the boundary of this conductor and calculating the current by an integration of an area of conductor ${\ensuremath{\Gamma}}_i$ :

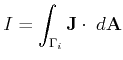$$I = \int_{{\ensuremath{\Gamma}}_i} \ensuremath{\mathbf{J}} \cdot d\ensuremath{\mathbf{A}}$$ (9.7)

or by calculating the electrical power loss:

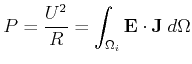$$P = \frac{U^2}{R}= \int_{{\ensuremath{\Omega}}_i} \ensuremath{\mathbf{E}} \cdot \ensuremath{\mathbf{J}} d{\ensuremath{\Omega}}$$ (9.8)

Similar to the capacitance calculation, the electric field $\ensuremath{\mathbf{E}}$ has to be calculated. The lack of sources of the electrical current density $\mathrm{div} \left( \ensuremath{\mathbf{J}} \right) = 0$ in the electrostatic system is also retained. Then the following equation for the current density is obtained, where ${\ensuremath{\Omega}}$ is the inside of a current-carrying conductor:

$$\mathrm{div} \left( \gamma \; \mathrm{grad} \left( {\ensuremath{\varphi}} \right) \right) = 0 \quad \textnormal{on} \; {\ensuremath{\Omega}}$$ (9.9)

$$\ensuremath{\mathbf{n}} \cdot \gamma \mathrm{grad} \left( {\ensuremath{\varphi}} \right) = 0 \quad \textnormal{on} \; {\ensuremath{\Gamma}}$$ (9.10)

$${\ensuremath{\varphi}} = {\ensuremath{\varphi}}_k \quad \textnormal{on} \; {\ensuremath{\Gamma}}_{k}$$ (9.11)

where ${\ensuremath{\Omega}}$ is a bounded open domain. ${\ensuremath{\Gamma}}$ is identified by the part of the boundary of ${\ensuremath{\Omega}}$ which is fully covered by isolators and not carrying any contacts, because there is no current flow from the conductor into the isolator $\ensuremath{\mathbf{J}} \cdot \ensuremath{\mathbf{n}} = 0$ . The contact areas ${\ensuremath{\Gamma}}_k$ normally carry a potential ${\ensuremath{\varphi}}_k$ . The finite element equation system is given for $N$ -elements by:

$$\sum_{j=1}^{N} {\ensuremath{\varphi}}_j \int_{\ensuremath{\tau_{3... ...{3}^{i}}} {\ensuremath{\phi}}_p {\ensuremath{\phi}}_q  d{\ensuremath{\Gamma}}$$ (9.12)

9.2.3 Finite Element Solution Procedure

To obtain the global solution, a procedure where all the local matrices have to be inserted into the global system matrix $\ensuremath{\mathbf{A}}$ is used, called assembly. Equation 9.6 as well as Equation 9.12 evaluated on all elements of a domain can then be expressed by a matrix notation:

$$\ensuremath{\mathbf{A}} \ensuremath{\mathbf{x}}=\ensuremath{\mathbf{b}}$$ (9.13)

where $\ensuremath{\mathbf{A}}$ is the global system matrix, $\ensuremath{\mathbf{x}}$ the solution vector, and $\ensuremath{\mathbf{b}}$ the right-hand side. A transformation of the local indices to global indices is required to obtain consistent system matrix entries.

The right-hand side matrix $\ensuremath{\mathbf{b}}$ is obtained by contributions of elements on the boundary of the domain, thereby only containing values not equal to zero for boundary contact nodes. A detailed notation of Equation 9.13 is given by [114]:

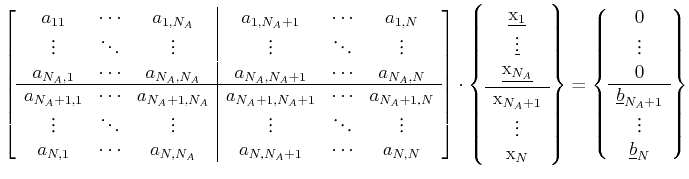$$\left[\begin{array}{ccc\vert ccc} a_{11} &\cdots&a_{1,N_A} &a_{1,... ... \hline \underline b_{N_A+1} \vdots \underline b_N \end{array}\right\}$$ (9.14)

where the upper half corresponds to the inner nodes whereas the lower half can be identified by the boundary nodes. The unknown values are underlined. Expressed as block matrices the equation system reads:

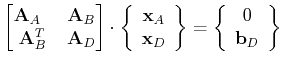$$\begin{bmatrix}\ensuremath{\mathbf{A}}_A\phantom{{}^T} & \ensurem... ...}=\left\{\begin{array}{c} 0 \ensuremath{\mathbf{b}}_D \end{array}\right\}$$ (9.15)

To obtain the unknown values $\ensuremath{\mathbf{x}}_A$ inside the domain, the equation system has to be solved:

$$\ensuremath{\mathbf{A}}_A \ensuremath{\mathbf{x}}_A = - \ensuremath{\mathbf{A}}_B  \ensuremath{\mathbf{x}}_{D}$$ (9.16)

The electric charge is then obtained by:

$$\ensuremath{\mathbf{b}}_D = \ensuremath{\mathbf{A}}_B^T \ensuremath{\mathbf{x}}_A + \ensuremath{\mathbf{A}}_D  \ensuremath{\mathbf{x}}_D$$ (9.17)

and solving:

$$\ensuremath{\mathbf{B}} \ensuremath{\mathbf{\sigma}} = \ensuremath{\mathbf{b}}$$ (9.18)

where $\ensuremath{\mathbf{B}}$ is built up from the local element matrices of the boundary elements.

9.2.4 Transformation into GSSE 

The transformation of the given expression is supported by GSSE's finite element components, given in Section 7.3.4. The following set of operations is required to obtain the solution:

1. Computation of the stencil matrices $\Pi(\ensuremath{\tau_{3}^{i}})$ and matrix $\ensuremath{\mathbf{b}}$ .
2. Assembly of the global system matrix $\ensuremath{\mathbf{A}}$ and matrix $\ensuremath{\mathbf{b}}$ .
3. Solution of the algebraic equation system $\ensuremath{\mathbf{A}} \ensuremath{\mathbf{x}}=\ensuremath{\mathbf{b}}$ .

Where the first step is already implemented in the GSSE . The second and third step are given in the following source snippet for two- and three-dimensional simplex and cuboid cell complexes:

The final line invokes the solver using the generic solver interface. Because of the library-centric application design approach of the GSSE and the derived applications, the matrix_type can be implemented by any matrix data structures, e.g., the high performance Blitz++ [150] matrices, or the C++ valarray. A performance comparison is given in Section 7.4.