Next: 2.3 Dielektrische Abschirmung von Ladungen Up: 2 Theorie der Störstellenstreuung Previous: 2.1 Ladungsverteilung von räumlich ausgedehnten Störstellen
![]()
![]()
![]()
Next: 2.3
Dielektrische Abschirmung von Ladungen Up: 2
Theorie der Störstellenstreuung Previous: 2.1
Ladungsverteilung von räumlich ausgedehnten Störstellen
Bis jetzt haben wir angenommen, daß das
gestreute Elektron immer nur mit einer einzigen Störstelle wechselwirkt
und haben dabei den Einfluß aller anderen Störstellen vernachlässigt.
Wir haben also das Vielteilchenproblem auf ein Zweiteilchenproblem reduziert.
Mit zunehmender Dotierung verringert sich der mittere Abstand zwischen
den Störstellen (Anhang A), sodaß
diese Näherung ihre Gültigkeit verliert. Wir wollen uns in weiterer
Folge auf die Einfachstreuung eines Elektrons an zwei Störstellen
beschränken, da das Streuproblem an mehr als zwei Zentren analytisch
nicht mehr berechenbar ist. Streuung an zwei ungleichnamig geladenen Streuzentren
(Dipol-Streuung) wurde schon in den 60er Jahren behandelt
[Str62,Boa65,CG82,RM85].
Literatur zur Paarstreuung findet sich in
[Moo67a,Moo67b,GR78,MB83b,JF91,KT91,JF92]
 |
Es mögen sich zwei Störstelle im mittleren Abstand ![]() voneinander entfernt befinden. Die Berechnung des mittleren Abstands zweier
benachbarter Störstellen ist nicht unumstritten, da sie von der Unterteilung
des betrachteten Volumens abhängt. Eine physikalisch plausiblere
Möglichkeit wird im Anhang A diskutiert.
Die Ladungsdichte dieser benachbarten Störstellen lautet nach (2.1)
voneinander entfernt befinden. Die Berechnung des mittleren Abstands zweier
benachbarter Störstellen ist nicht unumstritten, da sie von der Unterteilung
des betrachteten Volumens abhängt. Eine physikalisch plausiblere
Möglichkeit wird im Anhang A diskutiert.
Die Ladungsdichte dieser benachbarten Störstellen lautet nach (2.1)
| |
(2.8) |
wobei wir der Einfachheit halber nur Störstellen eines Typs angenommen
haben. Das durch das Störstellenpaar erzeugte Potential lautet gemäß
(2.5)
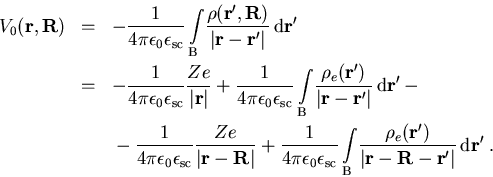 |
(2.9) |
Die Poisson-Gleichung (2.4) für
zwei Störstellen wird dann zu
| |
(2.10) |
Übergang in den Impulsraum nach (2.6)
ergibt schließlich das Gesamtpotential zweier gleichnamig geladener,
räumlich ausgedehnter Störstellen im Abstand ![]()
| |
(2.11) |
Wäre die Störstelle im Vakuum, dann ergäbe (2.11)
das Potential, an dem Leitungselektronen gestreut werden. In Silizium jedoch
sind die Störstellen an einem Gitterplatz gebunden, sodaß vier
Valenzelektronen gebunden sind. Daher bekommt man das effektive Streupotential,
indem man von (2.11) noch jenes Potential abzieht,
welches durch die Ladungsverteilung der Si-Atome erzeugt wird, da das Potential
des Halbleiters in der Bandstruktur schon berücksichtigt ist. Das
effektive Streupotential ist daher
| |
(2.12) |
Der erste Term im Zähler stellt den effektiven Kernanteil, der zweite den Elektronenanteil am Streupotential dar. Durch die Annahme einer punktförmigen Störstelle wurde die Ausdehnung des Elektronenanteils immer vernachlässigt. Man beachte, daß im Falle von P-dotiertem Silizium der Elektronenanteil wirklich verschwindet, da ein einfach-ionsiertes P-Atom gleichviele Elektronen wie ein Si-Atom hat. Setzt man für Z und N die Werte des jeweiligen Halbleiters ein, so muß das Streupotential verschwinden, da in einem intrinsischen Halbleiter keine Störstellenstreuung möglich ist. In den bisherigen Überlegungen wurde das Vorhandensein von freien Ladungsträgern vollkommen vernachlässigt. Wir werden im nächsten Abschnitt sehen, daß das effektive Streupotential in einem Festkörper wesentlich geringer ist, da frei bewegliche Leitungselektronen die ionisierte Störstelle teilweise abschirmen. Dadurch wird die effektive Ladung der Störstelle und damit deren Potentialstärke erheblich reduziert.