Next: 2.4 Born-Wirkungsquerschnitt erster Ordnung Up: 2 Theorie der Störstellenstreuung Previous: 2.2 Simultane Streuung an zwei räumlich ausgedehnten Störstellen
![]()
![]()
![]()
Next: 2.4
Born-Wirkungsquerschnitt erster Ordnung Up: 2
Theorie der Störstellenstreuung Previous: 2.2
Simultane Streuung an zwei räumlich ausgedehnten Störstellen
Wenn man in einem elektrisch neutralen Festkörper eine Ladung (zum Beispiel eine ionisierte Störstelle) einfügt, induziert diese ein lokales elektrisches Potential, welches andere bewegliche Ladungen veranlaßt, dieses lokale Potential abzuschirmen. Dieses dielektrische Verhalten des Elektronengases unter einer äußeren Störung wird als ,,screening`` bezeichnet. Arbeiten über den Einfluß der dielektrischen Abschirmung auf die Beweglichkeit finden sich in [Tak59,McI60,Hal62,Alf77,BK84,SDO85,CF88,BSM92,KKL93,Sch94].
Nehmen wir an, eine äußere Störung ![]() wirkt auf unser Elektronensystem. Die induzierten Konzentrationsschwankungen
wirkt auf unser Elektronensystem. Die induzierten Konzentrationsschwankungen
![]() des Elektronengases sind über die Poisson-Gleichung
des Elektronengases sind über die Poisson-Gleichung
| |
(2.13) |
mit einem inneren Potential verbunden sind. Das gesamte auf ein Elektron
wirkende Potential ist dann
| (2.14) |
Das innere Potential Vi beschreibt die abschirmende
Wirkung des Elektronengases auf das herausgegriffene Elektron. Das Verhältnis
zwischen Va und Vi, welches frequenz-
und wellenzahlabhängig ist, bezeichnet man als longitudinale Dielektrizitätskonstante
des Elektronengases. Man kann nun zeigen [Mad72],
daß sich das totale Streupotential im Impulsraum schreiben läßt
als
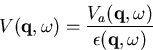 |
(2.15) |
mit
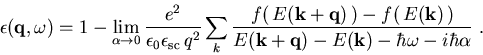 |
(2.16) |
Das ist die Lindhardsche dielektrische Funktion, die auf linearer Abschirmung
beruht. Voraussetzung dafür ist, daß das Verhältnis aus
potentieller Energie des Elektrons im Feld des Streupotentials und seiner
kinetischen Energie klein ist. Außerdem wurde bei der Herleitung
von (2.16) von einem Einteilchen-Hamiltonoperator
ausgegangen. Das Elektron reagiert also in dieser Näherung wie ein
freies Teilchen auf ein mittleres Potential ![]() [KF89].
[KF89].
Im Fall der Störstellenstreuung haben wir es mit einem statischen
Potential zu tun, sodaß ![]() und die Dämpfungskonstante
und die Dämpfungskonstante ![]() gegen Null gehen. Damit erhalten wir
gegen Null gehen. Damit erhalten wir
![\begin{displaymath}\epsilon (\vec{q},0)= 1 +\frac{e^2}{\epsilon_{0}\epsilon_{\m... ...k})} - \frac{1}{E(\vec{k}) - E(\vec{k} - \vec{q}) }\right]\; .\end{displaymath}](img321.gif) |
(2.17) |
Unter Verwendung von
und durch Ersetzen der Summation durch eine Integration nach (1.67)
erhalten wir schließlich [Fer91]
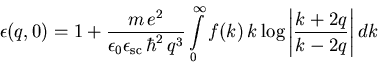 |
(2.18) |
Als Verteilungsfunktion wird die Gleichgewichtsverteilung nach Fermi-Dirac
angenommen. Nach Übergang auf die Variablen ![]() und x mit
und x mit
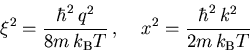 |
(2.19) |
erhalten wir schließlich
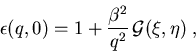 |
(2.20) |
wobei die Abschirmfunktion ![]() (Abb. 4.1) gegeben ist durch
(Abb. 4.1) gegeben ist durch
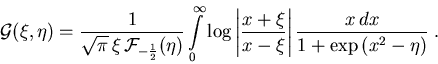 |
(2.21) |
Die inverse Thomas-Fermi-Abschirmlänge ![]() ist definiert durch (Anhang D)
ist definiert durch (Anhang D)
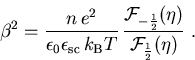 |
(2.22) |
Das Fermi-Integral j-ter Ordnung ![]() ist definiert als [Bla82]
ist definiert als [Bla82]
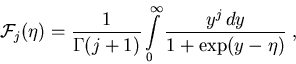 |
(2.23) |
wobei ![]() die reduzierte Fermi-Energie ist.
die reduzierte Fermi-Energie ist.
Damit lautet das totale effektive Streupotential, das ein Paar räumlich
ausgedehnter Störstellen mit gleicher Ladung unter Berücksichtigung
der dielektrischen Abschirmung in einem Festkörper beliebiger Entartung
erzeugt [KGKS97,KKGS97]
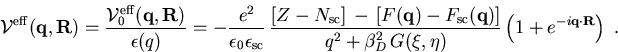 |
(2.24) |
(2.24) stellt die Basis dar zur Berechnung von Wirkungsquerschnitt und Streurate der Wechselwirkung zwischen Elektron und ionisierter Störstelle.
Der Begriff Potential ist etwas irreführend, da 2.24 dimensionsmäßig eine Energie darstellt. Bei der Herleitung von 2.24 mit Hilfe von 2.13 geht man von einem Streupotential aus, welches durch eine Ladungsverteilung induziert wird. Bei der Berechnung des Streuquerschnitts ist jedoch die potentielle Energie, die das gestreute Elektron in diesem Störpotential besitzt, maßgeblich.