2.4 Born-Wirkungsquerschnitt erster Ordnung

 Die Born-Streuamplitude erster Ordnung für ein Paar ionisierter Störstellen lautet mit (1.20) unter Verwendung von (2.24)

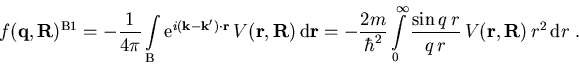$$f(\vec{q},\vec{R})^{\mathrm{B1}}= -\frac{1}{4\pi}\int {\math... ...r}\,U^{\mathrm{eff}}(\vec{r},\vec{R})\,r^2\,{\mathrm{} d}r\; .$$ (2.25)

Man beachte, daß die Born-Amplitude erster Ordnung sehr wohl das Vorzeichen des Störpotentials berücksichtigt. Erst bei der Bildung des Absolutquadrats zur Berechnung des Wirkungsquerschnitts verschwindet das Vorzeichen, wenn man von einer Punktladung ausgeht.

Zwischen der Born-Streuamplitude erster Ordnung $f^{\mathrm{B1}}$ und dem Potential ${\cal V}^{\mathrm{eff}}$ besteht die Relation

$$f^{\mathrm{B1}} = \frac{2m}{\hbar^2}\,{\cal V}\; .$$ (2.26)

Der differentielle Wirkungsquerschnitt ist nach (1.3) das Absolutquadrat der Streuamplitude (2.26):

$$\sigma (\vec{q},\vec{R}) = {\left\vert f(\vec{q},\vec{R})\right\vert}^2 = f (\vec{q},\vec{R})\cdot f^{*} (\vec{q},\vec{R})$$ (2.27)

Man beachte, daß f(q) im Allgemeinen komplex ist. Wir erhalten daher aus (2.24)

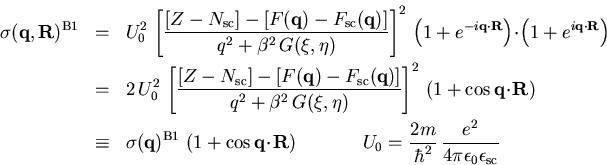$$\begin{eqnarray}\sigma (\vec{q},\vec{R})^{\mathrm{B1}} & =& U_{0}^2 \,\left[ ... ...{2m}{\hbar^2}\,\frac{e^2}{4\pi\epsilon_{0}\epsilon_{\mathrm{sc}}}\end{eqnarray}$$ (2.28)

Da alle Störstellen zufällig verteilt sind, ist keine Richtung ausgezeichnet, sodaß man eine Mittelung über die Orientierung von $\vec{R}$ mittels

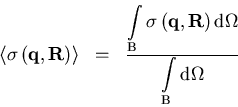$$\begin{eqnarray}\langle \sigma \left(\vec{q} ,\vec{R}\right) \rangle & = & \frac... ...} ,\vec{R}\right) {\mathrm{} d}\Omega }{\int {\mathrm{} d}\Omega}\end{eqnarray}$$ (2.29)

durchführt. Schließlich erhält man

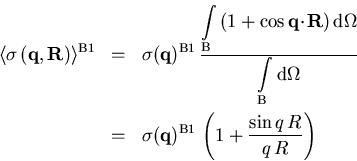$$\begin{eqnarray}\langle \sigma \left(\vec{q} ,\vec{R}\right) \rangle^{\mathrm{B... ...(\vec{q})^{\mathrm{B1}}\,\left( 1+\frac{\sin q\,R}{q\,R} \right)\end{eqnarray}$$ (2.30)

vornimmt. (2.30) stellt den mittleren differentiellen Streuwirkungsquerschnitt $\sigma (\vec{q},R)^{\mathrm{B1}}$ in der ersten Born-Näherung für ein Paar gleichnamig geladener Störstellen im Abstand $R=\vert\vec{R}\vert$ dar.