2.5 Thomas-Fermi Atom Modell

 Der im letzten Abschnitt hergeleitete Ausdruck (2.24) für das Streupotential zweier benachbarter, räumlich ausgedehnter Störstellen in einem dotiertem Halbleiter ist exakt, wenn man von Mehrfachstreuungen absieht. Um jedoch den differentiellen Wirkungsquerschnitt (2.30) der ionisierten Störstellenstreuung von Elektronen an einem bestimmten Dopanden berechnen zu können, benötigen wir neben der räumlichen Verteilung der Störstellen auch den Formfaktor des entsprechenden Dopanden, also die räumliche Ladungsverteilung seiner Valenz- und Kernelektronen. Da wir an analytischen Ausdrücken interessiert sind, bedienen wir uns des klassischen Atommodells von Thomas [Tho27] und Fermi [Fer27] zur Berechnung der Ladungsdichte, wobei wir jedoch die Ladungsdichte durch Variation des totalen Energiefunktionals und nicht über die TF Gleichung berechnen wollen. Das ursprüngliche TF Modell hat seit damals viele Verbesserungen erfahren [GSD71], sodaß man schließlich durch Hinzunahme einer Austauschkorrektur nach Dirac [Dir30] und einer Gradientenkorrektur zur kinetischen Energie nach Weizsäcker [vW35] eine bemerkenswert erfolgreiche (TFDW) Theorie zur Verfügung hat, die für große Ordnungszahlen exakt mit quantenmechanischen Modellen übereinstimmt [Thi90]. Das TF Atommodell geht von einem entarteten Fermigas bei Null Kelvin aus, das in einem konstant positiven Untergrund eingebettet ist [Gom49,Sca96]. Die Ladung der Valenz- und Kernelektronen wird also kontinuierlich verteilt angenommen und kann als eine Atmosphäre um die Kerne betrachtet werden. Durch die vollständige Entartung erhält man eine lokale Beziehung zwischen der Elektronendichte und der Fermienergie. Dieses statistische Atommodell des entarteten Elektronengases liefert etwa überraschenderweise genaue Ergebnisse für die Ionisationsenergien verschiedener Atome [KG73], kann jedoch Phänomene, die auf individuellen Eigenschaften einzelner Elektronen beruhen, naturgemäß nicht erklären (Periodensystem). Die hohe Entartung der Valenz- und Kernelektronen dürfte der Grund dafür sein, daß die Näherung des Elektronensystems durch ein entartetes Fermi-Gas bei Null Kelvin überraschend gut ist [FST86].

Das Grundproblem bildet nun die Bestimmung der Potentialverteilung der Elektronen eines atomaren Systems. Die Lösung dieses Problems fanden unabhängig voneinander unter den obigen Annahmen Thomas [Tho27] und Fermi [Fer27]. Da die TF-Gleichung nur numerisch lösbar ist, bedienen wir uns des Ritz'schen Variationsverfahrens zur Bestimmung der Ladungsdichte. Genauso wie man die Schrödinger-Gleichung aus einem Variationsprinzip herleiten kann, läßt sich auch die TF-Gleichung aus einem Variationsansatz herleiten, indem man das totale Energiefunktional bildet [Len32]. Man gibt eine beliebige Ladungsverteilung mit zunächst unbestimmten Parametern vor und berechnet die totale Energie. Die Parameter werden dadurch bestimmt, daß die Energie ein Minimum annehmen muß. Je besser die gewählte Ladungsdichte der echten entspricht, desto genauer ist der erhaltene Wert für die minimale Energie, die der experimentell gemessenenen Ionisierungsenergie im Grundzustand entspricht. Der Variationsansatz ist der herkömmlichen TF-Methode, die sich der TF-Gleichung bedient, überlegen, da man durch entsprechende Wahl von Funktionen der quantenmechanischen Lösung sehr nahe kommt.

Die totale Energie E des Systems setzt sich zusammen aus der klassischen elektrostatischen Energie $E_{\rm{e}-\mathrm{e}}$ aufgrund der Elektron-Elektron-Wechselwirkung, der Coulomb-Energie $E_{\mathrm{e}-\mathrm{n}}$ aufgrund der Elektron-Kern-Wechselwirkung, der kinetische Energie $E_{\mathrm k}$, einer Inhomogenitätskorrektur $E_{\mathrm w}^{\mathrm{inh}}$ für the kinetische Energie [vW35] und einer quantenmechanischen Austauschkorrektur $E_{\mathrm{ex}}$ [Dir30]:

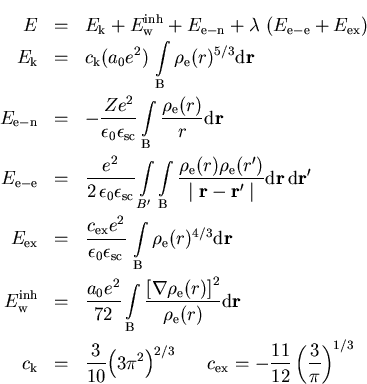$$\begin{eqnarray}E&=&E_{\mathrm k}+E_{\mathrm w}^{\mathrm{inh}}+E_{ \mathrm{e}-\m... ...mathrm{ex}}=-\frac{11}{12} \,{\left( \frac{3}{\pi} \right)}^{1/3}\end{eqnarray}$$ (2.31)

wobei a₀ der klassische Bohr-Radius ist (Anhang A). Bei der Berechnung von $E_{ \rm{e}-\mathrm{e} }$ wird vernachlässigt, daß ein Elektron nicht auf sich selbst wirken kann. Der Korrelationsparameter $\lambda$, der immer kleiner als eins ist, wird eingeführt, um diesen Fehler auszugleichen. Durch Nullsetzen der partiellen Ableitungen von $E(N,Z,\alpha_{1},\alpha_{2},\ldots, \alpha_{n} )$ nach den n Variationsparametern $\alpha_{i}$

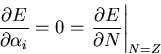$$\begin{eqnarray}\frac{\partial E}{\partial \alpha_{i}}=0=\left.\frac{\partial E}{\partial N}\right\vert _{N=Z}\end{eqnarray}$$ (2.32)

erhält man ein Gleichungssystem vom Rang n+1, woraus man die unbestimmten Parameter $\alpha_{i}$ und $\lambda$ in eindeutiger Weise erhält. Die letzte Gleichung spiegelt das Verschwinden des chemischen Potentials eines neutrales Atom im TF Modell wider [Thi90].
 

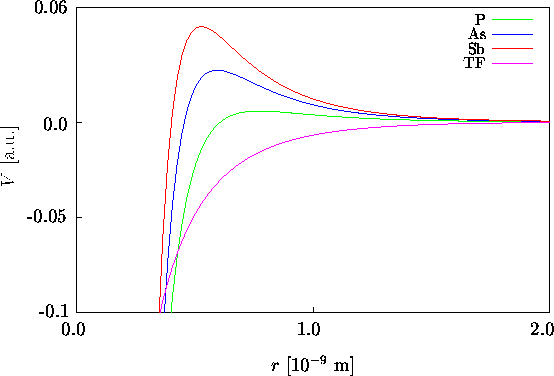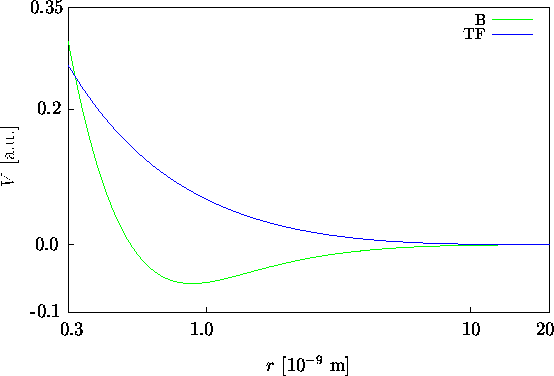
Wir wollen in weiterer Folge eine geschirmte Coulomb-Verteilung annehmen, die die quantenmechanisch berechnete Ladungsdichte, die für große r exponentiell abklingt, besser wiedergibt als die Lösung der TF-Gleichung, die zu langsam abklingt. Die normierte, exponentiell abgeschirmte Ladungsdichteverteilung und der entsprechende Formfaktor für N Valenz- und Kernelektronen lautet

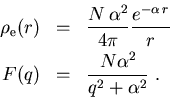$$\begin{eqnarray}\rho_{\mathrm e} (r)&=& \frac{N\,\alpha^2}{4 \pi} \frac{{\mathrm... ...alpha \, r}}{r}\\ F(q) &=& \frac{N\alpha^2}{q^2+\alpha^2} \; .\end{eqnarray}$$ (2.33)

Wenn wir nun (2.33) in (2.31) einsetzen, erhalten wir für die totale Energie

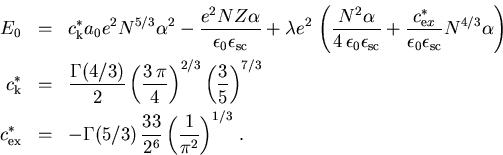$$\begin{eqnarray}E_{0}&= & c_{\mathrm k}^{*}a_{0}e^2 N^{5/3} \alpha^2- \frac{e^2N... ...(5/3)\,\frac{33}{2^6}\,{\left( \frac{1}{\pi^2}\right)}^{1/3} \; .\end{eqnarray}$$ (2.34)

Berechnungen haben interessanterweise gezeigt, daß die mit Hilfe von (2.34) erhaltenen Grundzustandsenergien nicht notwendigerweise besser sind als jene, die mit dem ursprünglichen TF Energiefunktional berechnet werden, das keine quantenmechanischen Korrekturen enthält [Sca96]. Nach Minimierung von (2.34 erhalten wir für $\alpha$

$$\begin{eqnarray}\alpha &=&\frac{Z^{1/3}}{c_{\mathrm k}^{*}a_{0}\epsilon_{0}\eps... ...3}} \right] }{\frac{5}{3}-4\,\left( \frac{Z}{N}\right)^{1/3}}\; .\end{eqnarray}$$ (2.35)

Damit erhalten wir für den Korrelationsparameter

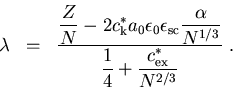$$\begin{eqnarray}\lambda & =& \frac{\frac{Z}{N} - 2 c_{\mathrmk}^{*}a_{0}\epsilo... ...{1/3}} }{\frac{1}{4} +\frac{c_{\mathrm{ex}}^{*}}{N^{2/3}} } \; .\end{eqnarray}$$ (2.36)

$\alpha^{-1}$ ist ein Maß für die mittlere räumliche Ausdehnung der Ladungsverteilung der Valenz- und Kernelektronen der Störstelle.
 

 

• 2.5.1 Erste Born-Näherung
• 2.5.2 Zweite Born-Näherung