2.5.2 Zweite Born-Näherung

Die Streuamplitude zweiter Ordnung ist nach (1.40)

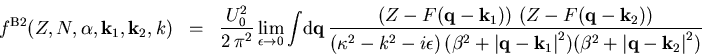$$\begin{eqnarray}f^{\mathrm{B2}}(Z,N,\alpha,\vec{k}_{1},\vec{k}_{2},k)&= & \frac{... ...t}^2 )( \beta^{2}+{\vert\vec{q}-\vec{k}_{2} \vert}^2) }\nonumber\end{eqnarray}$$ (2.40)

Wenn wir als Ladungsverteilung (2.33) heranziehen, kann man nach einigen rationalen Transformationen alle Integrationen ausführen (Anhang C), sodaß man

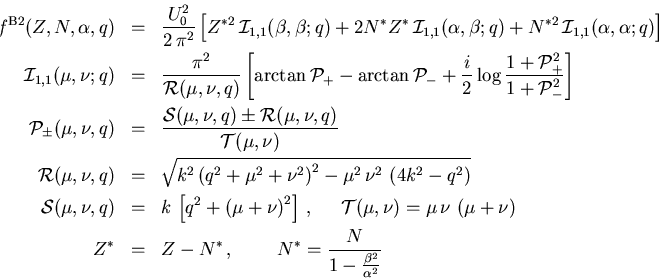$$\begin{eqnarray}\!\! f^{\mathrm{B2}}(Z,N,\alpha ,q)&\!\! =\!\!& \frac{U_{0}^2}{... ..., , \;\;\;\;\;\;\;\; N^{*}= \frac{N}{1-\frac{\beta^2}{\alpha^2}} \end{eqnarray}$$ (2.41)

erhält. In [Lew56] wird nur der Realteil von (2.41) abgeleitet. Die vollständige zweite Born-Streuamplitude (2.41) für eine räumlich ausgedehnte Ladungsverteilung (2.33) wurde meines Wissens noch nie publiziert.

Wenn wir den Grenzübergang $\alpha \rightarrow \infty$ durchführen, erhalten wir aus (2.41) den Ausdruck (1.46) für eine punktförmige Ladung [Joa75].

Verschiedene Streuamplituden zweiter Ordnung für unterschiedliche Potentiale finden sich in [Mow52]. Man erkennt, daß die Imaginärteile von (2.41) und (1.46) für verschwindende Abschirmung divergieren und damit der differentielle Wirkungsquerschnitt in der zweiten Born-Näherung unendlich wird. Bei fehlender Abschirmung jedoch stellt der Born-Wirkungsquerschnitt erster Ordnung den exakten Wirkungsquerschnitt dar. Es sei daran erinnert, daß die Born-Reihe als Potenzreihenentwicklung nach der Potentialstärke $\gamma$ interpretiert werden kann. Für die Streuamplitude erhalten wir dann

$$f = \gamma f_{1} + \gamma^2 f_{2} + \ldots \; .$$ (2.42)

Damit ergibt sich für den differentiellen Wirkungsquerschnitt [Moi74]

$$\sigma = \gamma^2 f_{1}^2 +2 \gamma^3 {\cal R}(f_{1}\cdot f_... ...2}\vert^2 + 2 \gamma^4 {\cal R}( f_{1}\cdot f_{3}) \ldots \; ,$$ (2.43)

wobei ${\cal R}$ für den Realteil steht. Man erkennt, daß ein Term vierter Ordnung in $\gamma$ von der dritten Born-Amplitude herrührt. Dieser Term kompensiert exakt den divergenten Imaginärteil der zweiten Born-Amplitude, sodaß bei verschwindender Abschirmung in (2.43) alle Terme höher als zweiter Ordnung in $\gamma$ gegen Null gehen.