Next: 1.3.3 Variationsmethode nach Schwinger Up: 1.3 Integraldarstellung des Streuproblems Previous: 1.3.1 Fredholm-Methode
![]()
![]()
![]()
Next: 1.3.3
Variationsmethode nach Schwinger Up: 1.3
Integraldarstellung des Streuproblems Previous: 1.3.1
Fredholm-Methode
Man kann die Gleichung (1.20) auch direkt
ohne Kenntnis der Streuphasen erhalten. Falls in (1.1)
die Störung ![]() ,,klein``
in der Weise ist, daß
,,klein``
in der Weise ist, daß
| (1.35) |
gilt, kann man ![]() in eine Potenzreihe nach
in eine Potenzreihe nach ![]() entwickeln
entwickeln
| |
(1.36) |
Durch Gleichsetzen gleicher Ordnungen in ![]() von (1.1) und (1.36)
erhält man folgendes Gleichungssystem:
von (1.1) und (1.36)
erhält man folgendes Gleichungssystem:
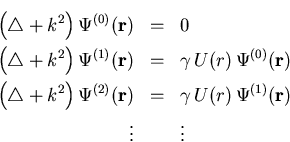 |
(1.37) |
welches immer noch exakt ist. In erster Ordnung erhalten wir als Lösungsfunktion
die ebene Welle. In zweiter Ordnung erhalten wir für ![]()
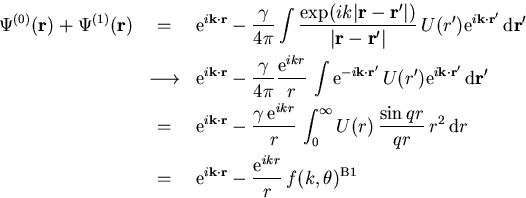 |
(1.38) |
Durch Vergleich mit (1.20) erkennt man also, daß wir mit Hilfe der Wellenfunktion der Ordnung n die Streuamplitude der Ordnung n-1 erhalten.
Um höhere Ordnungen der Streuamplitude zu berechnen, ist es einfacher
direkt von der Integraldarstellung der Streumamplitude i'ter Ordnung
auszugehen, die folgende Form [Joa75,Møl30]
hat:
| (1.39) |
Die Green-Funktion kann als Propagator interpretiert werden, der auf
das Elektron wirkt. In zweiter Ordnung erhalten wir
| |
(1.40) |
Das Elektron im Zustand ![]() wechselwirkt mit dem Potential U, wobei es in den Zustand
wechselwirkt mit dem Potential U, wobei es in den Zustand ![]() übergeht. Nachdem es ein zweites Mal mit dem Potential wechselwirkt,
bewegt es sich mit dem Zustand
übergeht. Nachdem es ein zweites Mal mit dem Potential wechselwirkt,
bewegt es sich mit dem Zustand ![]() weiter. Für ein geschirmtes Coulomb-Potential der Form
weiter. Für ein geschirmtes Coulomb-Potential der Form
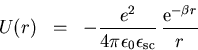 |
(1.41) |
lassen sich die Matrixelemente leicht berechnen, sodaß wir
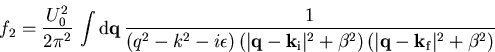 |
(1.42) |
erhalten, wobei wir ![]() definiert haben. Unter Benützung der Feynman-Identität (Anhang
C)
definiert haben. Unter Benützung der Feynman-Identität (Anhang
C)
![\begin{displaymath}\frac{1}{a\, b} = \int\limits_{0}^{1} \frac{{\mathrm d}t }{\left[ a\,t +b\, \left( 1-t \right) \right]^2}\end{displaymath}](img179.gif) |
(1.43) |
läßt sich (1.42) schreiben
als
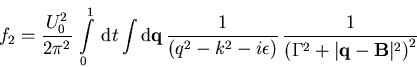 |
(1.44) |
wobei ![]() gilt. Im Anhang C wird gezeigt, daß
man (1.44) schreiben kann als
gilt. Im Anhang C wird gezeigt, daß
man (1.44) schreiben kann als
| (1.45) |
Man erhält schließlich für die Born-Amplitude zweiter
Ordnung einer punktförmigen Ladung folgenden Ausdruck [Joa75]
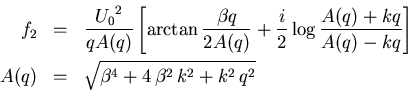 |
(1.46) |