Next: 1.3.2 Born-Näherung als sukzessive Approximation Up: 1.3 Integraldarstellung des Streuproblems Previous: 1.3 Integraldarstellung des Streuproblems
![]()
![]()
![]()
Next: 1.3.2
Born-Näherung als sukzessive Approximation Up: 1.3
Integraldarstellung des Streuproblems Previous: 1.3
Integraldarstellung des Streuproblems
Die Lösung des Streuproblems (1.1)
führte uns auf die Integralgleichung (1.26)
für ![]() .
Diese kann nach Fredholm allgemein geschrieben werden als
.
Diese kann nach Fredholm allgemein geschrieben werden als
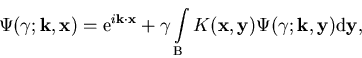 |
(1.30) |
mit dem Kern
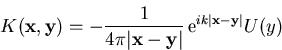 |
(1.31) |
(1.30) wird als Fredholm-Gleichung bezeichnet
[WO75]. ![]() ist eine Konstante, die die Stärke des Potentials charakterisiert.
Das Streuproblem ist nun reduziert auf die Lösung einer Integralgleichung
der Form (1.30) mit einem Potential U,
das im Kern (1.31) vorkommt. Bei einem gegebenen
physikalischen Problem ist U gegeben, sodaß wir
ist eine Konstante, die die Stärke des Potentials charakterisiert.
Das Streuproblem ist nun reduziert auf die Lösung einer Integralgleichung
der Form (1.30) mit einem Potential U,
das im Kern (1.31) vorkommt. Bei einem gegebenen
physikalischen Problem ist U gegeben, sodaß wir ![]() eins setzen können. Von einem allgemeineren mathematischen Standpunkt
wollen wir jedoch
eins setzen können. Von einem allgemeineren mathematischen Standpunkt
wollen wir jedoch ![]() als Parameter der Integralgleichung betrachten. Nach Fredholm kann die
Lösung von (1.30), falls eine solche
existiert, geschrieben werden als
als Parameter der Integralgleichung betrachten. Nach Fredholm kann die
Lösung von (1.30), falls eine solche
existiert, geschrieben werden als
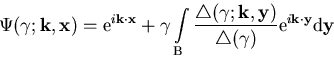 |
(1.32) |
mit
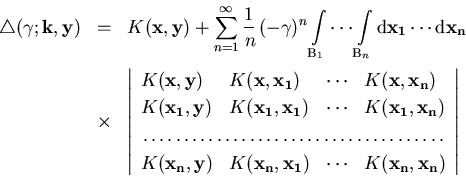 |
(1.33) |
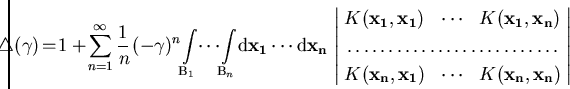 |
(1.34) |
Man kann zeigen, daß die beiden Reihen ![]() und
und ![]() für jedes
für jedes ![]() konvergieren vorausgesetzt, daß
konvergieren vorausgesetzt, daß ![]() stetig ist [WO75], wenn also links- und rechtsseitiger
Grenzwert existieren und identisch sind. Falls
stetig ist [WO75], wenn also links- und rechtsseitiger
Grenzwert existieren und identisch sind. Falls ![]() ,
dann gibt (1.33) und (1.34)
eingesetzt in (1.32) die Lösung von
(1.30).
,
dann gibt (1.33) und (1.34)
eingesetzt in (1.32) die Lösung von
(1.30).
Bei Streuproblemen ist der Kern (1.31)
singulär für ![]() .
Man kann diese Singularität umgehen, indem man
.
Man kann diese Singularität umgehen, indem man ![]() und
und ![]() in (1.32) formal mit
in (1.32) formal mit ![]() multipliziert, sodaß wir Ausdrücke für
multipliziert, sodaß wir Ausdrücke für ![]() und
und ![]() erhalten, in denen alle
erhalten, in denen alle ![]() ,
,
![]() gleich Null werden [JP51,MF53b].
gleich Null werden [JP51,MF53b].