Next: 1.3.1 Fredholm-Methode Up: 1 Theoretische Grundlagen der Streuung Previous: 1.2 Streuphasenanalyse

1.3 Integraldarstellung des Streuproblems

Nach Abschnitt 1.1 kann die Schrödinger-Gleichung (1.1) in kompakter Form geschrieben werden als

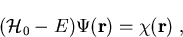$\begin{displaymath} ({\cal{H}}_{0}-E) \Psi(\vec{r})=\chi(\vec{r}) \; , \end{displaymath}$

(1.21)

wobei

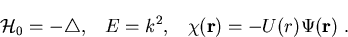$\begin{displaymath}{\cal{H}}_{0}=- \bigtriangleup ,\;\;\;E=k^2, \;\;\;\chi(\vec{r})=-U(r)\Psi(\vec{r})\; . \end{displaymath}$

(1.22)

Die formale Lösung dieser partiellen Differentialgleichung lautet [MF53b]

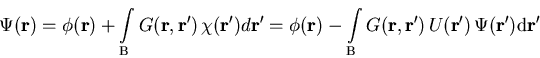$\begin{displaymath} \Psi(\vec{r})=\phi (\vec{r})+\int G (\vec{r},\vec{r'})\,\chi... ...r},\vec{r'})\,U(\vec{r'} )\,\Psi(\vec{r'}) {\mathrm d}\vec{r'} \end{displaymath}$

(1.23)

wobei sich der Integrationsbereich B ins Unendliche erstreckt. Wir wollen daher in weiterer Folge annehmen, daß alle uneigentlichen Integrale existieren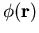. $\phi (\vec{r})$ ist eine partikuläre Lösung der homogenen Gleichung

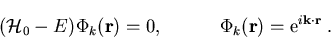$\begin{displaymath}({\cal{H}}_{0}-E) \Phi_{k}(\vec{r}) =0,\qquad\quad \Phi_{k}(\vec{r})={\mathrm e}^{i\vec{k}\cdot \vec{r}}\; . \end{displaymath}$

(1.24)

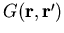$G (\vec{r},\vec{r'})$ ist die Green-Funktion von 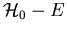${\cal{H}}_{0}-E$ . Es gilt

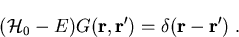$\begin{displaymath}({\cal{H}}_{0}-E) G (\vec{r},\vec{r'})=\delta (\vec{r}-\vec{r'})\; . \end{displaymath}$

(1.25)

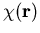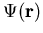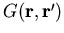Da $\chi(\vec{r})$ die unbekannte Funktion $\Psi(\vec{r})$ beinhaltet, stellt (1.23) die Schrödinger-Gleichung in Integralform dar. Der Vorteil von (1.23) gegenüber (1.1) liegt daran, daß durch geeignete Wahl von $G (\vec{r},\vec{r'})$ in (1.23) die gewünschte Randbedingung (1.2) automatisch erfüllt wird [WO75]. Im Fall von auslaufenden (+) oder einlaufenden (-) Wellen erhalten wir folgende Lösung für (1.23):

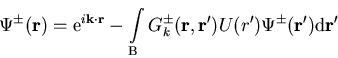$\begin{displaymath} \Psi^{\pm}(\vec{r})={\mathrm e}^{i\vec{k}\cdot\vec{r}} -\int... ...ec{r},\vec{r'}) U (r') \Psi^{\pm}(\vec{r'}){\mathrm d}\vec{r'} \end{displaymath}$

(1.26)

mit

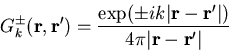$\begin{displaymath} G_{k}^{\pm} (\vec{r},\vec{r'})=\frac{\exp (\pm ik\vert\vec{r}-\vec{r'} \vert)}{4\pi \vert\vec{r}-\vec{r'} \vert} \end{displaymath}$

(1.27)

In Operatorform lautet (1.26)

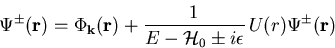$\begin{displaymath} \Psi^{\pm}(\vec{r})=\Phi_{\vec{k}}(\vec{r})+\frac{1}{E-{\cal{H}}_{0}\pm i\epsilon} \, U (r) \Psi^{\pm}(\vec{r}) \end{displaymath}$

(1.28)

mit

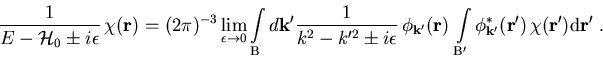$\begin{displaymath} \frac{1}{E-{\cal{H}}_{0}\pm i\epsilon}\,\chi(\vec{r})=(2\pi)... ...'}}^{\ast}(\vec{r'}) \,\chi (\vec{r'}) {\mathrm d}\vec{r'}\; . \end{displaymath}$

(1.29)

Die Größe 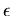$\epsilon$ in (1.28) und (1.29) wird als Hilfsgröße eingeführt, um die Singularität bei der Integration zu umgehen. Die Integralgleichung (1.26) kann nun mit verschiedenen Methoden gelöst werden. Man kann die Lösungsfunktion 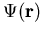$\Psi(\vec{r})$ durch sukzessive Iteration erhalten oder sich verschiedener Variationsmethoden bedienen [Moi66].

Next: 1.3.1 Fredholm-Methode Up: 1 Theoretische Grundlagen der Streuung Previous: 1.2 Streuphasenanalyse

Kaiblinger-Grujin Goran
1997-12-06