6.5.1 Performance

For the investigation of the computational and storage demands of the stabilized march algorithm the required numerical operations have to be analyzed. In Table 6.5 a summary over the involved steps is given. The order of the computational costs of the QR-factorization can be found in [202, p. 225] and of the LU-factorization in [202, p. 98]. For the IVP integration we consider the special structure of the system matrix in (6.32) showing that only half of the unknowns are coupled to the derivatives of the other half. Hence, the number of operations to be performed is proportional to the number of unknowns times the number of couplings times the number of discretization points. The storage costs for the matrix operations are determined by the matrix size. For the IVP integration the initial values are only required at the opposite boundary point. The BVP solution is of course stored for all discretization points. Consequently, during the determination of the initial values they are solely proportional to the number of unknowns, whereas only for the final BVP integration they also depend on the vertical mesh size.

 

Table 6.5: Numerical costs of the stabilized march algorithm. The second column indicates the corresponding step number in Table 6.4, in the third column the required evaluations are counted, the third column describes the storage demands, and in the fourth column the order of the computational costs for one evaluation are given.

 

Operation	Step	Counts	Storage	CPU
QR-factorization of a NODE x NODE/2 matrix	1 & 2.b	Np	NODE2/2	NODE3/2
IVP integration to obtain NODE/2 linearly independent solutions	2.a	NODE/2	NODE	NODE2/2 x Nz
LU-factorization of a NODE/2 x NODE/2 matrix	3	1	NODE2/4	NODE3/8
IVP integration to obtain Ns BVP solutions	4	Ns	NODE x Nz	NODE2/2 x Nz

The following notation is used: N_ODE stands for the order of the ordinary differential equation system, N_s signifies the number of boundary conditions, N_p denotes the number of shooting intervals, and N_z is the number of discretization points in the whole simulation interval [0, h].

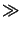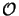The computational costs can be gathered from Table 6.5 by multiplying the costs of each operation with its counts. Since the order N_ODE of the ODE is large in comparison to the number of vertical discretization points N_z, the number of source points N_s, and the number of shooting intervals N_p, i.e., N_ODE $\gg$ N_z, N_s, N_p, they are proportional to $\mathcal {O}$(N_z x N_ODE³/4) as can be seen from the second row of Table 6.5. Hence, most of the computational effort in the stabilized march algorithm goes into the IVP integrations. The application of reduced superposition is thus of crucial importance since the number of required IVP integrations is halved. 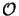The second largest expense are the N_p QR-factorizations requiring $\mathcal {O}$(N_p x N_ODE³/2) operations. The additional costs 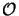$\mathcal {O}$(N_ODE³/8) of the LU-factorization due to the multiple BCs resulting from the distributed source are negligible, which is one of the major advantages of the proposed implementation of the differential method.

The memory demands of the algorithm are dominated by the storage of the linearly independent solution matrix as can be seen from Table 6.5 and thus grow with 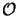$\mathcal {O}$(N_ODE²/2). The counts do not to have be considered here since the solution is propagated recursively through the simulation interval by the marching technique. Hence, also the entire memory demands of the stabilized march algorithm are proportional to 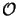$\mathcal {O}$(N_ODE²/2).

This discussion shows that the overall performance is roughly characterized by

 

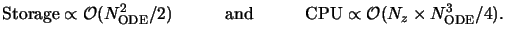$$\text{Storage}\propto \mathcal{O}(N_{\mathrm{ODE}}^2/2) {}\quad\q... ...nd}\quad\qquad{}\text{CPU}\propto \mathcal{O}(N_z \times N_{\mathrm{ODE}}^3/4).$$ (6.51)

Exact figures for run-time and storage consumption are given in combination with the presentation of simulation results in Chapter 8. Typical values lie around four to five hours of run-time on a DEC-600/333 workstation and 200 to 400 MB of memory. The performance figures given in (6.77) are in accordance with those presented in Table 5.1 and are of the same order as for the waveguide method.