Next: 6.5.3 Comparison with the
Up: 6.5 Discussion
Previous: 6.5.1 Performance
There are two sources of limitations of the differential method, namely,
computational requirements that are getting too large and failure of the
stabilized march
technique due to strongly damped solution modes resulting in
numerical instabilities.
The first can be overcome by an increase of the
available computer resources, e.g., with the next computer
generation it will be possible to solve problems of double size.
The second, however, is a principle limitation and thus more serious.
We will discuss both impacts from a qualitative point of view.
Computational Requirements.
In (6.77) is shown that the computational costs and
storage demands grow with the second and the third orders of the number
NODE of the Fourier coefficients considered, respectively.
Since
NODE is determined by the two truncation frequencies
Nx and Ny of the Fourier expansion of the lateral field components
(cf. (6.29)), they should be chosen as small as possible.
The physical impacts of the truncation cause a low-pass filtering of the field
as well as of the geometry and have already been discussed in
Section 6.2.5. An analytical investigation of a lateral
stepped
permittivity including error-bounds is presented in Appendix D.
Hence, there is a fundamental tradeoff between computational
requirements and accuracy. To be more precise we have to answer the
question of how many Fourier modes are required to represent the EM field
with a precision that is high enough. For that we reconsider the
sampling of the lateral wavevectors introduced in (6.13)
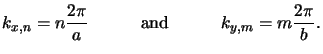 |
(6.52) |
The following considerations are performed for a homogeneous medium only.
However, the results are useful for a qualitative study of a general
inhomogeneous medium. Denoting the permittivity of the medium by
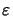 =
= 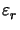 + j
+ j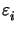 the vertical wavevector component writes to
whereby
k0 = 2
the vertical wavevector component writes to
whereby
k0 = 2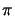 /
/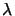 is inserted for the wavenumber.
Since the vertical dependence
Enm(z) of the EM field is
an exponential one, i.e., we have plane waves due to the homogeneity
and thus
Enm(z)
is inserted for the wavenumber.
Since the vertical dependence
Enm(z) of the EM field is
an exponential one, i.e., we have plane waves due to the homogeneity
and thus
Enm(z) 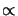 exp(jkz, nmz),
it is described by a damped oscillating function like
exp(jkz, nmz),
it is described by a damped oscillating function like
![$\displaystyle \mathbf{E}_{nm}(z) \propto e^{j\operatorname{Re}[k_{z,nm}]z} e^{-\operatorname{Im}[k_{z,nm}]z}.$](img1023.gif) |
(6.54) |
The oscillation period
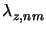 and the penetration depth
and the penetration depth
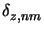 are simply given by
are simply given by
![$\displaystyle \lambda_{z,nm} = \frac{2\pi}{\operatorname{Re}[k_{z,nm}]}\quad\qquad\text{and}\quad\qquad\delta_{z,nm} = \frac{1}{\operatorname{Im}[k_{z,nm}]},$](img1026.gif) |
(6.55) |
whereby the real and imaginary parts of kz, nm are calculated
from (6.79) to
with
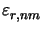 defined as the real part of (cf. (6.79))
defined as the real part of (cf. (6.79))
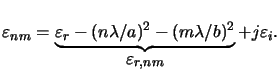 |
(6.56) |
We are now interested in the minimal values of both, the
oscillation period
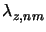 and the penetration depth
and the penetration depth
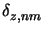 , depending on the index pair (n, m). This means that
we have to determine (n, m) for which
Note that minimal penetration depth means maximal damping.
From (6.82) we see that
Re[kz, nm] is a monotone
increasing function whereas
Im[kz, nm] is a monotone decreasing function
with respect to
, depending on the index pair (n, m). This means that
we have to determine (n, m) for which
Note that minimal penetration depth means maximal damping.
From (6.82) we see that
Re[kz, nm] is a monotone
increasing function whereas
Im[kz, nm] is a monotone decreasing function
with respect to
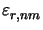 , i.e.,
, i.e.,
![$\displaystyle \frac{\partial \operatorname{Re}[k_{z,nm}]}{\partial \varepsilon_...
...ad\frac{\partial \operatorname{Im}[k_{z,nm}]}{\partial \varepsilon_{r,nm}} < 0.$](img1034.gif) |
(6.57) |
The extreme values are thus given by (cf. (6.84))
whereby Nx and Ny are the truncation frequencies of the Fourier
expansions of the EM field. The mode (0, 0) propagating in vertical direction
exhibits the highest oscillation and the least damping,
whereas the four most oblique ones
( 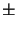 Nx,
Nx, 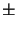 Ny) are least oscillating
but strongest damped--a result that is physically reasonable.
Hence the oscillating nature of the EM field is reflected by the ODE system
independently of the
truncation frequencies. The truncation frequencies have
to be chosen in a way that also damped modes are resembled with sufficient
precision. But the higher Nx and/or Ny are, the stronger
the damping becomes, which causes stability problems of the algorithm. Before we
consider this problem another consequence from (6.86)
shall be discussed. As can be seen the ratio between wavelength
Ny) are least oscillating
but strongest damped--a result that is physically reasonable.
Hence the oscillating nature of the EM field is reflected by the ODE system
independently of the
truncation frequencies. The truncation frequencies have
to be chosen in a way that also damped modes are resembled with sufficient
precision. But the higher Nx and/or Ny are, the stronger
the damping becomes, which causes stability problems of the algorithm. Before we
consider this problem another consequence from (6.86)
shall be discussed. As can be seen the ratio between wavelength 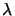 and the lateral dimensions a and b of the simulation domain determines
and the lateral dimensions a and b of the simulation domain determines
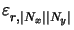 and thus also the imaginary part
Im[kz,| Nx|| Ny|]
of the vertical wavevector component (cf. (6.82)).
These ratios are the critical quantities for the choice of appropriate
truncation frequencies, i.e.,
and thus also the imaginary part
Im[kz,| Nx|| Ny|]
of the vertical wavevector component (cf. (6.82)).
These ratios are the critical quantities for the choice of appropriate
truncation frequencies, i.e.,
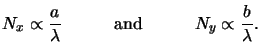 |
(6.58) |
The rank of the resulting ODE system and thus the computational
requirements are determined by it. For example, in the simulation results
presented in Chapter 8 this ratio was approximately four, i.e.,
for 248 nm lithography the lateral extensions were 1 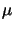 m. This shows
that the differential method is only suited for single feature simulation,
a situation that applies to all rigorous EM field solvers.
m. This shows
that the differential method is only suited for single feature simulation,
a situation that applies to all rigorous EM field solvers.
Numerical Instabilities. Numerical instabilities are caused by
damped solution modes. The preceding discussion shows that there are two reasons
for the existence of such modes, namely, a strongly absorptive medium
and high truncation frequencies. The first is self-evident, whereas the
second results from the fact that for larger Nx and/or Ny the real part
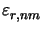 of the permittivity
of the permittivity
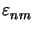 becomes negative
(cf. (6.83)). These modes are then called evanescent
since in a loss-less medium with
becomes negative
(cf. (6.83)). These modes are then called evanescent
since in a loss-less medium with
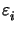 = 0 they propagate in lateral direction
and are damped vertically, i.e., in the orthogonal direction to the propagation
direction. In a lossy or absorbing medium with
= 0 they propagate in lateral direction
and are damped vertically, i.e., in the orthogonal direction to the propagation
direction. In a lossy or absorbing medium with
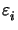 > 0 the real part
Re[kz, nm] of the vertical component of the wavevector almost vanishes
whereas the negative part
Im[kz, nm] becomes dominating. In the limiting
case
| Nx|
> 0 the real part
Re[kz, nm] of the vertical component of the wavevector almost vanishes
whereas the negative part
Im[kz, nm] becomes dominating. In the limiting
case
| Nx| 
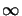 and
| Ny|
and
| Ny| 
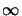 we have
Re[kz, nm]
we have
Re[kz, nm]  0 and/or
Im[kz, nm]
0 and/or
Im[kz, nm] 
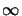 .
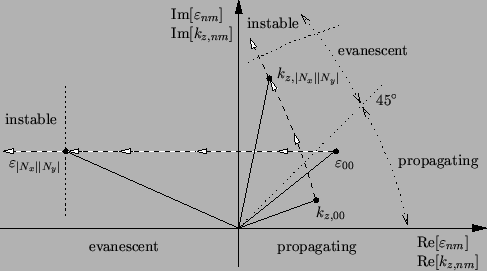
This situation is graphically illustrated in Figure 6.6.
For a proper function of the stabilized march algorithm the truncation
frequencies have to be chosen carefully so that all propagating modes are
accounted for, but at most only a few evanescent ones are considered.
.
This situation is graphically illustrated in Figure 6.6.
For a proper function of the stabilized march algorithm the truncation
frequencies have to be chosen carefully so that all propagating modes are
accounted for, but at most only a few evanescent ones are considered.
The discussion shows that the truncation of the EM field expansion is
crucial for the operation of the differential method--not just for the
computational requirements but also for the convergence of the algorithm.
The same situation applies to the waveguide model, since it it is actually
a special case of the differential method as will be shown in the next section.
Figure 6.6:
The truncation frequencies Nx and
Ny in the differenital method have to be chosen so that all propagating
modes are reflected by the solution, whereas only a small number of
evanescent modes can be considered since they might cause numerical
instabilities.
|
|




Next: 6.5.3 Comparison with the
Up: 6.5 Discussion
Previous: 6.5.1 Performance
Heinrich Kirchauer, Institute for Microelectronics, TU Vienna
1998-04-17
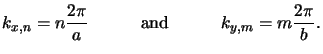
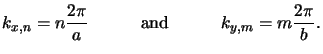
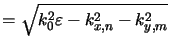
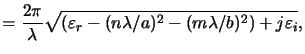
![$\displaystyle \lambda_{z,nm} = \frac{2\pi}{\operatorname{Re}[k_{z,nm}]}\quad\qquad\text{and}\quad\qquad\delta_{z,nm} = \frac{1}{\operatorname{Im}[k_{z,nm}]},$](img1026.gif)
![$\displaystyle \begin{aligned}\operatorname{Re}[k_{z,nm}] &= \sqrt{\frac{+\varep...
...varepsilon_{r,nm}+\sqrt{\varepsilon_{r,nm}^2+\varepsilon_i^2}}{2}}\end{aligned}$](img1027.gif)
![$\displaystyle \begin{alignedat}{2}\lambda_{z,nm} &\longrightarrow\max \qquad&\o...
...angle}{=}\qquad\operatorname{Im}[k_{z,nm}] &\longrightarrow\max.\end{alignedat}$](img1032.gif)
![$\displaystyle \frac{\partial \operatorname{Re}[k_{z,nm}]}{\partial \varepsilon_...
...ad\frac{\partial \operatorname{Im}[k_{z,nm}]}{\partial \varepsilon_{r,nm}} < 0.$](img1034.gif)
![]() of the permittivity
of the permittivity
![]() becomes negative
(cf. (6.83)). These modes are then called evanescent
since in a loss-less medium with
becomes negative
(cf. (6.83)). These modes are then called evanescent
since in a loss-less medium with
![]() = 0 they propagate in lateral direction
and are damped vertically, i.e., in the orthogonal direction to the propagation
direction. In a lossy or absorbing medium with
= 0 they propagate in lateral direction
and are damped vertically, i.e., in the orthogonal direction to the propagation
direction. In a lossy or absorbing medium with
![]() > 0 the real part
Re[kz, nm] of the vertical component of the wavevector almost vanishes
whereas the negative part
Im[kz, nm] becomes dominating. In the limiting
case
| Nx|
> 0 the real part
Re[kz, nm] of the vertical component of the wavevector almost vanishes
whereas the negative part
Im[kz, nm] becomes dominating. In the limiting
case
| Nx| ![]()
![]() and
| Ny|
and
| Ny| ![]()
![]() we have
Re[kz, nm]
we have
Re[kz, nm] ![]() 0 and/or
Im[kz, nm]
0 and/or
Im[kz, nm] ![]()
![]() .
This situation is graphically illustrated in Figure 6.6.
For a proper function of the stabilized march algorithm the truncation
frequencies have to be chosen carefully so that all propagating modes are
accounted for, but at most only a few evanescent ones are considered.
.
This situation is graphically illustrated in Figure 6.6.
For a proper function of the stabilized march algorithm the truncation
frequencies have to be chosen carefully so that all propagating modes are
accounted for, but at most only a few evanescent ones are considered.