



Next: 7. Photoresist Bake and
Up: 6.5 Discussion
Previous: 6.5.2 Limitations
6.5.3 Comparison with the Waveguide Method
Since the waveguide model is the second frequency domain method close
similarities exist to the differential method. In fact we will
show that the waveguide model equals the differential method if
a zeroth-order vertical discretization scheme is used for the solution
of the BVP. Hence the differential method comprises the waveguide model and
is thus superior to it.
For that we reconsider (6.32). By comprising the four lateral
vectors
ex(z),
ey(z),
hx(z), and
hy(z) carrying the relevant Fourier coefficients
(cf. (6.30)) into two new vectors
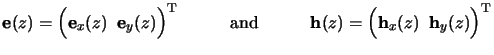 |
(6.59) |
we can rewrite the ODE system (6.32) to
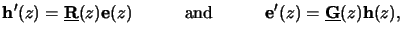 |
(6.60) |
whereby the two matrices
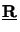 (z) and
(z) and
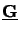 (z) are given by
(z) are given by
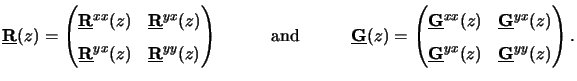 |
(6.61) |
In the waveguide method the medium is divided into
thin layers with vertically constant refractive
index [8,190,69,73,186,187,188]. The
two matrices are assumed to be constant within such a layer, i.e.,
for
z 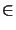 [zl, zl + 1]
[zl, zl + 1]
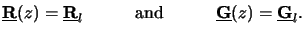 |
(6.62) |
One vector of unknowns, e.g.,
h(z), can thus simply be eliminated
from the ODE system (6.89). By differentiating
the left equation of (6.89) and inserting the right
equation of (6.89) we obtaing
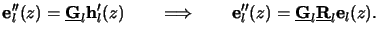 |
(6.63) |
The system matrix of the reduced second-order ODE system has a constant
coefficient matrix
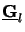
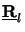 . We set it equal to the
square
. We set it equal to the
square
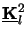 of a matrix
of a matrix
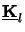 , i.e., the
NODE/2-dimensional second-order ODE system
, i.e., the
NODE/2-dimensional second-order ODE system
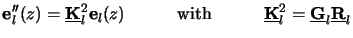 |
(6.64) |
has to be solved
within one layer
z  [zl, zl + 1]. This ODE system corresponds to the
Helmholtz equation (4.2), whereby the wavenumber k is
replaced by the matrix
[zl, zl + 1]. This ODE system corresponds to the
Helmholtz equation (4.2), whereby the wavenumber k is
replaced by the matrix
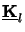 . Note that the system matrix has to
be normal to write it as the square
. Note that the system matrix has to
be normal to write it as the square
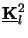 of another matrix
since only then an eigenvalue decomposition exists, and a matrix
of another matrix
since only then an eigenvalue decomposition exists, and a matrix
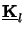 can be found so that
can be found so that
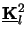 =
= 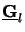
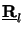 .h
The existence
proof of the normal property of
.h
The existence
proof of the normal property of
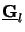
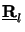 as well as the
calculation of the square root
as well as the
calculation of the square root
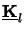 =
= 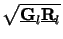 can both be performed with the help of (6.22). Since we are only
interested in a theoretical comparison the actual numerical evaluation is of
minor interest. The formal solution of (6.93) is given
by [203, pp. 937-947]
can both be performed with the help of (6.22). Since we are only
interested in a theoretical comparison the actual numerical evaluation is of
minor interest. The formal solution of (6.93) is given
by [203, pp. 937-947]
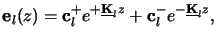 |
(6.65) |
whereby the matrix exponential
exp( 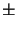
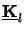 z) can be calculated with
the methods described in [202, pp. 572-577].
z) can be calculated with
the methods described in [202, pp. 572-577].
The solution (6.94) of the ODE
system (6.93) corresponds to the solution of the
eigenvalue problem occurring in the waveguide
model [187, eq. (33)]. Since the matrix exponential can also be
evaluated by an eigenvalue decomposition,i both
methods--waveguide and zeroth-order differential--involve the same numerical
operations and thus require the same computational costs. All other steps
like matching the solutions of adjacent layers to determine
the coefficient vectors
cl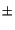 of (6.94) and
thereby propagating the
solution through the whole simulation interval are equal. This proves
theoretically that the differential method comprises the
waveguide model as a sub-class, i.e., as the zeroth-order approximation.
of (6.94) and
thereby propagating the
solution through the whole simulation interval are equal. This proves
theoretically that the differential method comprises the
waveguide model as a sub-class, i.e., as the zeroth-order approximation.
As a direction for future work it would be interesting to compare both methods
numerically. For a fair and correct benchmark a zeroth-order discretization
scheme should be implemented for the differential method. This can be done
most efficiently by determining the solution (6.94)
of (6.93) since otherwise the higher order discretization
is compared with the zeroth-order discretization of the waveguide model.
Our implementation is not optimized for that purpose and the benchmark could
potentially yield misleading results.
Footnotes
- ... obtaing
- Also for vertically
dependent matrices the vector
h(z) can be eliminated
from (6.89) yielding
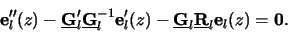 Future research has to be done to investigate whether a direct solution of the
above second-order ODE is advantageous to our implementation which solves
the corresponding first-order ODE.
Future research has to be done to investigate whether a direct solution of the
above second-order ODE is advantageous to our implementation which solves
the corresponding first-order ODE.
- ....h
- The eigenvalue
decomposition of a normal matrix
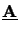 is given by
is given by
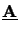 =
= 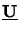
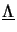
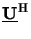 ,
whereby
,
whereby
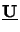 is a unitary matrix comprising the eigenvectors
is a unitary matrix comprising the eigenvectors
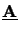 uj =
uj = 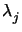 uj and
uj and
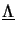 is a
diagonal matrix with the eigenvalues
is a
diagonal matrix with the eigenvalues 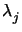 as diagonal entries. The square
root is defined as
as diagonal entries. The square
root is defined as
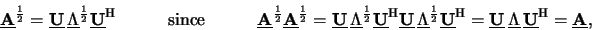 whereby the unitary property
whereby the unitary property
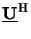
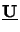 =
= 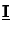 of
of
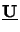 has been used and the square root
has been used and the square root
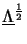 of the diagonal matrix
of the diagonal matrix
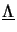 is simply given by taking the square root
is simply given by taking the square root
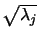 of the diagonal
entries
of the diagonal
entries 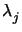 . Numerically more efficient and stable methods exist
to calculate the square root [202, pp. 572-577].
Note that any matrix polynomial
. Numerically more efficient and stable methods exist
to calculate the square root [202, pp. 572-577].
Note that any matrix polynomial
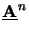 can be calculated similarly to the
square root, and thus a broad class of functions--including transcendental
ones like the exponential--can be calculated from their Taylor series
expansions.
can be calculated similarly to the
square root, and thus a broad class of functions--including transcendental
ones like the exponential--can be calculated from their Taylor series
expansions.
- ... decomposition,i
- See footnote
f on previous page.




Next: 7. Photoresist Bake and
Up: 6.5 Discussion
Previous: 6.5.2 Limitations
Heinrich Kirchauer, Institute for Microelectronics, TU Vienna
1998-04-17
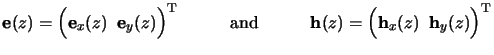
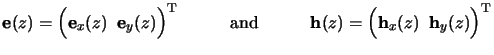
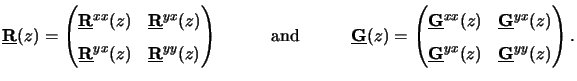
![]() of (6.94) and
thereby propagating the
solution through the whole simulation interval are equal. This proves
theoretically that the differential method comprises the
waveguide model as a sub-class, i.e., as the zeroth-order approximation.
of (6.94) and
thereby propagating the
solution through the whole simulation interval are equal. This proves
theoretically that the differential method comprises the
waveguide model as a sub-class, i.e., as the zeroth-order approximation.