5.2.5 Einfluß mechanischer Spannung

Next: 5.2.6 Kombination Up: 5.2 Effektive Masse Previous: 5.2.4 Dotierungsabhängigkeit

5.2.5 Einfluß mechanischer Spannung

Unter Einfluß mechanischer Verspannung wird auch die ansonsten isotrope effektive Masse des direkten 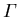$\varGamma$ Minimums anisotrop. Für den betrachteten Fall der biaxialen Spannung ergibt sich ein effektiver Masse Tensor mit zwei verschiedenen Komponenten in Richtung senkrecht und parallel zur Materialgrenzfläche. Aus Gleichung (5.41) erhält man

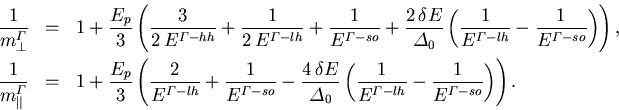$\begin{eqnarray} \frac{1}{m_{\perp}^{\varGamma}} &=& 1 + \frac{E_p}{3} \left(\f... ...E^{\varGamma-lh}}} - \frac{1}{{E^{\varGamma-so}}}\right)\right). \end{eqnarray}$

(5.50)

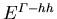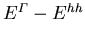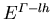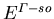${E^{\varGamma-hh}}$ steht für die Differenz ${E_{\mathrm{}}^{\varGamma}}-{E_{\mathrm{}}^{hh}}$ unter Spannungseinfluß, ${E^{\varGamma-lh}}$ und ${E^{\varGamma-so}}$ sind analog definiert.

Die Verspannungseinflüsse auf m können als additive Korrektur zur unverspannten Masse modelliert werden:

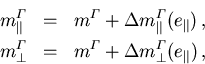$\begin{eqnarray} m_{\Vert}^{\varGamma} & = & {m_{}^{\varGamma}} + \Delta m_{\Ve... ...{\varGamma}} + \Delta m_{\perp}^{\varGamma}(e_\Vert)\,, \nonumber \end{eqnarray}$

(5.51)

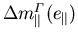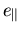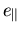wobei die Korrekturen der Komponenten $\Delta m_{\Vert}^{\varGamma}(e_\Vert)$ und $\Delta m_{\perp}^{\varGamma}(e_\Vert)$ durch die Verzerrung in ähnlicher Weise wie die Verschiebung der Bandkanten (5.24) durch einen Polynomausdruck in $e_\Vert$ mit materialabhängigen Koeffizienten geschrieben werden. Für GaInAs ergibt ein kubischer Ansatz mit parabolischer Materialabhängigkeit einen maximalen relativen Fehler unter 2% für den gesamten nutzbaren Bereich von $e_\Vert$ .Die DOS Masse kann in gleicher Weise approximiert werden:

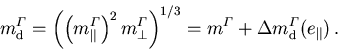$\begin{displaymath} {m_{\mathrm{d}}^{\varGamma}} = \left(\left(m_{\Vert}^{\varG... ...{\varGamma}} + \Delta {m_{\mathrm{d}}^{\varGamma}}(e_\Vert)\,. \end{displaymath}$

(5.52)

Die Koeffizienten der Interpolationspolynome sind in Tabelle 5.7 angeführt.

**Tabelle 5.7:** Koeffizienten zur Interpolation der Änderung der effektiven Masse von Ga_xIn_1-xAs unter (001) Spannung
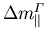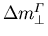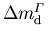	$\Delta m_{\Vert}^{\varGamma}$			$\Delta m_{\perp}^{\varGamma}$			$\Delta {m_{\mathrm{d}}^{\varGamma}}$
	x⁰	x¹	x²	x⁰	x¹	x²	x⁰	x¹	x²
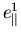$e_\Vert^1$	-0.319	0.132	-0.147	-0.33	-0.168	0.104	-0.321	0.0235	-0.041
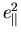$e_\Vert^2$	-3.65	11.21	-7.60	-2.10	-0.593	1.692	-3.051	5.932	-3.128
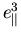$e_\Vert^3$	-10.50	164.0	-67.85	-25.86	-57.81	61.56	-12.95	74.47	-27.98

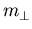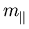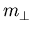Abbildung 5.6 zeigt einen Vergleich der exakten und approximierten Massenparameter. Man erkennt, daß durch kompressive Deformation sämtliche Werte erhöht werden, wobei $m_{\perp}^{}$ stärker als $m_{\Vert}^{}$ beeinflußt wird. Für tensile Verspannung sinken die Massen, wieder ist $m_{\perp}^{}$ stärker betroffen. Die Konsequenzen der Massenänderung auf den Stromtransport, die man aufgrund des beschriebenen Verhaltens erwartet, werden in Abschnitt 6.1.8 erläutert. 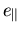Einen Vergleich mit den Berechnungen von Jaffe und Singh [97], die den Einfluß von $e_\Vert$ in einer ``tight-binding'' Bandstrukturberechnung in den Grundparametern berücksichtigen, zeigt Abbildung 5.7 für GaInAs pseudomorph auf GaAs. Die Übereinstimmung ist besonders bei 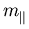$m_{\Vert}^{}$ sehr gut.

Der Einfluß der Verspannung auf die höheren indirekten LB Täler wird üblicherweise vernachlässigt. Die Anisotropie zufolge der Verschiebung der Minima, die in Abschnitt 5.1.4 erläutert wird, ist weitaus stärker ausgeprägt (siehe Abschnitt 6.1.9).

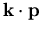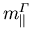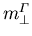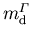**Abbildung 5.6:** Vergleich der mittels $\mbox{${\vec{k} \cdot \vec{p}}$}$ Theorie berechneten und approximierten Werte von $m_{\Vert}^{\varGamma}$ , $m_{\perp}^{\varGamma}$ und ${m_{\mathrm{d}}^{\varGamma}}$ für Ga_xIn_1-xAs
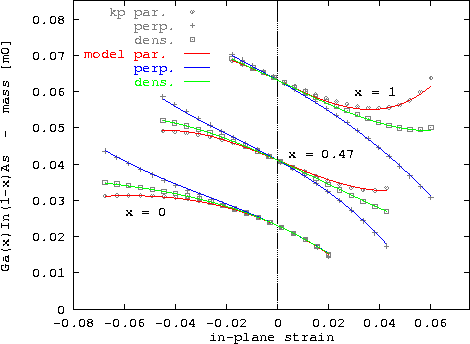$\begin{figure} \epsfxsize0.90\textwidth \centerline{\epsfbox{ps/GaInAs_mass_st... ...{${\vec{k} \cdot \vec{p}}$}$}\ Methode} \end{minipage} \end{center}\end{figure}$

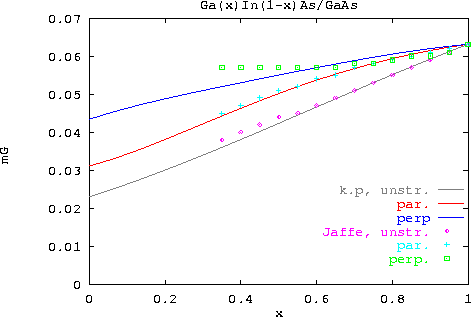
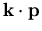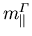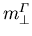**Abbildung 5.7:** Vergleich der mittels $\mbox{${\vec{k} \cdot \vec{p}}$}$ Theorie und ``tight-binding'' Methode berechneten Werte von $m_{\Vert}^{\varGamma}$ und $m_{\perp}^{\varGamma}$ für Ga_xIn_1-xAs auf GaAs
$\begin{figure} \epsfxsize0.90\textwidth \centerline{\epsfbox{ps/GaInAs_GaAs_mG... ...{${\vec{k} \cdot \vec{p}}$}$}\ Methode} \end{minipage} \end{center}\end{figure}$

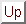
Next: 5.2.6 Kombination Up: 5.2 Effektive Masse Previous: 5.2.4 Dotierungsabhängigkeit

Christian Koepf
1997-11-11