| | |
To further introduce abstractions it is simplest to examine a few historical developments of the
abstractions involved in modelling space which is the omnipresent backdrop of any model of reality.
The nature of space has been under debate for considerable time, dating back to classical antiquity.
While the deeper mysteries of the true nature shall not be investigated here, the procedure of
constructing structural models using mathematics shall be touched upon. René Descartes, also known as
Renatus Cartesius, formalized, building on the work of his predecessors, the description of space using
the concepts of what we now call Cartesian coordinates, which are constructed by employing the
Cartesian product (Definition 3) of numbers. This seemingly simple abstraction allows to associate
space, or a portion thereof, to be associated with numbers. This, highly geometric, construction then
allows to examine the relations and the evolution of objects in space using the obtained numbers. Every
component of the Cartesian product needs to be considered individually, for as long as not the
notion of vector spaces (Definition 16) and vectors is established as a powerful entity which
allows for powerful yet concise expression. This step should not be underestimated, as simply
aggregating numbers to form a new entity, since not every collection of numbers results in a
vector, even when the reverse is true that an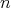 
-dimensional vector may be represented using
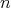numbers, which are to be understood to be in reference to a given base of the vector
space.
The described abstractions are easily compatible and were even driven by geometrical concepts as introduced by Euclid, hence naming such a space Euclidean. However, the consequent acceptance that our world is not flat, already reveals that this Euclidean concept of geometry is insufficient for larger scales, even if it performs marvellously in a local setting. An abstraction capable of carrying this structure was found in manifolds, since they by definition satisfy the local constraint, yet offer the flexibility required on a larger scale. It also explicitly shows how entities or concepts which were previously considered to be constant, need to be generalized in such a fashion, as to conserve local behaviour, while being globally variable.
With the further increase of sophistication of descriptions, which inherently demanded the use of manifolds, the study and classification of these constructs became a subject of interest. Following the seemingly ageless expression “divide et impera”, it proved prudent to decompose the previously opaque entity into geometric and topologic components. Such a decomposition should not be mistaken for the crude and brutal dissassembly of a vector into its components, since it aims to reveal previously hidden structure. The introduction of topology allows for a powerful and expressive classification of spaces, again by mapping to numbers, e.g., the Betti numbers.
The analysis of the structures of topological spaces (Definition 29) and manifolds (Definition 35) also spawned the concepts of fibrations (Definition 39) and fiber bundles (Definition 40) in particular, which provide a methodical means of constructing structures of increasing complexity from rudimentary building blocks. The fiber bundle for instance defines a simple attachment of virtually arbitrary quantities to a basic topological space in a structure preserving manner. Thus not only can manifolds be expressed using fiber bundles, but it is furthermore possible to also express quantities defined on these manifolds as fiber bundles again. Relations between different quantities as well as their evolution are then expressible as maps between fiber bundles. It is for its very basic yet powerful nature that it can be considered as the main abstraction for the definition of data structures in a digital computer in addition to its value in other fields.
| | |