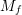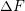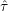5.5.1  Model Parameters

The acquisition of all necessary material parameters for the dislocation glide model is a great challenge. Most of the data available in the literature refer to bulk materials and thin film properties are usually very different. Moreover, the parameters are sensitive to the deposition methods and conditions, which hinder their general usability. Therefore, a safe approach is to obtain the parameters directly from stress measurements in a controlled thermal cycle experiment, as was performed for the presented experiment, in addition to the inclusion of previously available experimental data.

In order to obtain proper values for the material parameters, the dislocation glide model (5.8) must fit the stress measurements [85]. Since (5.8) is a differential equation, traditional fitting techniques based on gradient methods are not suitable. Therefore, a meta-heuristic optimization technique known as Genetic Algorithm (GA) was implemented [94][61]. The goal was to obtain a set of parameters (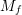, , 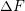, 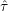and ), which minimizes the distance between the experimental and the computed stress at various temperatures. Hence, the objective can be described mathematically by

(5.9)

where 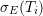is the experimental stress measured at temperature 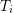and 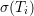is the stress computed by (5.8).

One drawback to this approach is the lack of evidence of the uniqueness of the solution of (5.9). This means that there is a chance that two different sets of parameters with different physical meaning can solve (5.9). However, during this work such a situation was not encountered. The obtained parameter values are summarized in Table 5.2. The calculated stress evolution with the obtained parameters is presented in Section 5.5.2 along with a comparison with experimental data.

Table 5.2.:

Parameters of the dislocation glide model obtained using a Genetic Algorithm (GA).

Parameter	Value
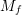(GPa)	555.85
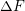(J)	2.8592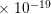
s	0.2119
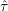(GPa)	1.9655