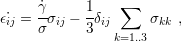
In order to have a thermo-mechanical simulation of the TSV, which properly considers the dislocation glide mechanism described in Section 5.4.2, (5.8) must be included in the thermo-elastic FEM model of the structure. The coupling must consider the breaking of the equibiaxial thin film assumption in the TSV and consequently, the stress computed in Section 5.4.2 must be related to the individual stress components. The relation is given by the associated flow rule:
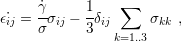 | (5.10) |
where 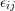 are the strain rate tensor components,
are the strain rate tensor components,  are the stress tensor components,
and
are the stress tensor components,
and  is the thin film stress computed by (5.8). It is possible to obtain the individual
components of the stress tensor by proceeding with a derivation for each component, similar
to that shown for (5.8). Thus, the evolution of the film stress components is described
by
is the thin film stress computed by (5.8). It is possible to obtain the individual
components of the stress tensor by proceeding with a derivation for each component, similar
to that shown for (5.8). Thus, the evolution of the film stress components is described
by
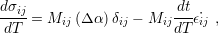 | (5.11) |
where 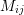 is the linear constant which relates the elastic strain to the stress
(Section 2.2.1). For the normal components,
is the linear constant which relates the elastic strain to the stress
(Section 2.2.1). For the normal components, 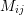 is equal to the biaxial modulus (
is equal to the biaxial modulus (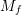 ).
The relation (5.11) is the generalization of (5.8) in order to include scenarios where the
equibiaxial condition cannot be assured.
).
The relation (5.11) is the generalization of (5.8) in order to include scenarios where the
equibiaxial condition cannot be assured.
The framework described by (5.8), (5.10) and (5.11) summarizes the entire physics required to design a simulation scheme to couple FEM with the dislocation glide model, including the cases where the equibiaxial assumption is not valid. The coupling strategy developed in this work is accomplished with the following procedure:
 .
.
The first initial stress in the tungsten layer in Step 1 is taken from an experimental value measured at room temperature (residual stress after deposition) [85]. In Step 2, (5.11) is solved using a backward differentiation formula (BDF) method. The simulation runs through the entire temperature cycle (heating and cooling).
Thermo-mechanical FEM simulations were performed for the standard open TSV and for full-plate sample structures. For the TSVs, scallops were included in the simulation. For both, (5.8) describes only the deformation for the tungsten layer, while the remaining materials are considered to have a simple thermo-elastic behavior.
The purpose of the full-plate simulation is to validate the coupling between the plastic and thermo-elastic model, and also to validate the parameters in Table 5.2. The experience acquired through this simulation regarding assumptions, numerical issues, meshing, and physical interpretation is then applied to the TSV simulation model.
The full-plate simulation was set up with symmetric boundary conditions in order to obtain a result as close as possible to a measurement carried out in the center of the full-plate sample. The computed stress evolution follows very closely the measured values and is only slightly skewed from the GA fitted curve, as shown in Fig. 5.19. This difference can be explained by the mechanical influence of the oxide and the silicon layers. With this simulation, the applied model, the parameter values obtained from the fitting process (Table 5.2), and the coupling scheme between the plastic and the thermo-elastic models were verified. To simulate the stress behavior inside the TSV, an axisymmetric boundary condition was assumed. The analysis was split into two parts due to the particular geometry of the TSV. The first part concerns the top of the TSV and the second part the middle of the TSV.
The top is distinguished by the additional non-constrained surfaces regularly present above the structure. The stress evolution at the tungsten layer is depicted in Fig. 5.20.
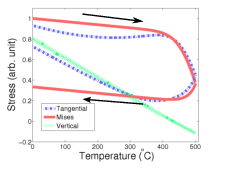
| Figure 5.20.: | Stress evolution at the TSV top for the metal layer. The stress in the vertical direction sustains an elastic behavior, because the stress level along the thermal cycle is not sufficient to activate the glide mechanism. |
Unlike the full-plate sample, in the case of the TSV a highly anisotropic stress distribution is observed. The thermal stress in the cylindrically shaped TSV superposes the expected stress evolution, leading to a fast decline of stress in the vertical direction and a very slow growth on the tangential direction. Hence, the von Mises stress has a peculiar behavior: during heating it follows the upper branch of the stress curve, as the stress component in the vertical direction of the TSV structure, and during the cooling it follows the bottom branch of this curve, as the stress component in the tangential direction.
The middle of the TSV experiences different effects at the top of the TSV structure. The only non-constrained surface is the TSV sidewall, thus the expansion of the material is more limited and the overall stress increases, as shown in Fig. 5.21. Moreover, during heating, the von Mises stress increases by approximately 10%, instead of decaying as was observed in the full-plate samples. Such an increase could be dangerous for the structure, since the residual stress in the tungsten layer is already very high and an additional tension could surpass the material’s ultimate strength, leading to cracks in the metal and a complete failure of the via.
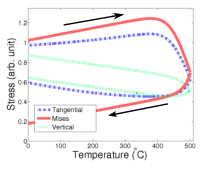
| Figure 5.21.: | Stress evolution at the TSV middle for the metal layer. The von Mises stress increases during heating and could damage the structure. |