next up previous contents
Next: 5.3 Case Study: Simulation Up: 5. Impact-Ionization Generation Previous: 5.1 Basics of Impact-Ionization

Subsections


5.2 Modeling Approaches

Only carriers with high energies contribute to the avalanche process. Like all high-energy mechanisms, impact-ionization is a non-local process (compare Section 4.3.1). This leads to problems in classical drift-diffusion simulation environments, because only local quantities are available, while no exact information on the distribution function can be obtained. Also hydrodynamic simulations deliver only the mean energy. Thus, the information on high-energy tails of the carrier distribution function is not available (see Section 4.3.2). As a result, drift-diffusion and/or hydrodynamic schemes require modeling approaches which are only based on local quantities.

5.2.1 Local Electric Field Based Modeling

In drift-diffusion simulations, the only local quantity that allows conclusions on the carrier temperature and therefore on the impact-ionization rate is the electric field. Many authors who investigated the ionization coefficients, both, experimentally and theoretically, suggested an exponential relation to the electric field $ E$ as [11]

$\displaystyle \ensuremath{\alpha _\nu}= \ensuremath{\alpha ^{\infty}}_\nu \exp ... ...ft( \frac{\ensuremath{E^{\mathrm{crit}}}_\nu}{E} \right)^{\beta_\nu} \right ] ,$ (5.13)

where the index $ \nu$ stands for electrons $ n$ and holes $ p.$ $ \ensuremath{\alpha ^{\infty}}_\nu$ and $ \ensuremath{E^{\mathrm{crit}}}_\nu$ are the high-field value of the ionization rate and the reference field, respectively. Although these quantities have certain physical meanings, commonly they are used as fitting parameters. This equation originates from the classic paper by Chynoweth [191], where the power $ \beta_\nu$ was assumed to be $ 1.$ In different modeling and experimental works, however, values of this exponent are found between 1 (Chynoweth [191] or Shockley [192]) and 2 (Wolff [193]). An important extension of this model was made including the electric field $ \ensuremath{\mathbf{E}}$ in the direction of the carrier flow, i.e. the current density $ \ensuremath{\mathbf{J}}.$ Therefore, the absolute value of the electric field $ E$ is often replaced by $ E = \ensuremath{E_{\vert\vert}}= \ensuremath{\mathbf{E}}\cdot \ensuremath{\mathbf{J}}_\nu / J_\nu$ [194,120].

An early approach deriving the value of the parameter $ \beta_\nu$ from the BTE was performed by Baraff [195]. He showed that the different values 1 and 2 used for $ \beta_\nu$ are the limiting cases for relatively low and high fields. However, there is no closed solution of his approach, but approximations have been presented in various publications, for example, by Crowell et al. [196],

$\displaystyle \ensuremath{\alpha _\nu}= \frac{1}{\lambda_\nu} \exp \left[ C_0(r) + C_1(r) x(E) + C_2(r) x(E)^2 \right] .$ (5.14)

In this formalism, $ r$ is the ratio between the average energy loss per collision $ \ensuremath{\mathcal{E}}_r$ and the ionization energy $ \ensuremath{\mathcal{E}}_i,$ $ r=\left.\ensuremath{\mathcal{E}}_r\middle/\ensuremath{\mathcal{E}}_i\right.,$ and $ x$ incorporates the mean free path $ \lambda $ between collisions with high energetic phonons and is defined as $ x(E)=\left.\ensuremath{\mathcal{E}}_i\middle/\ensuremath{\mathrm{q}}\lambda E\right..$ The coefficients $ C_i(r)$ are fitted to second order polynomial functions. This approximation fits the theoretical data from Baraff over a wide range of voltages. An improved approximation has been given by Sutherland [197] using additionally a third order term of $ x$ in (5.14) and for the coefficients $ C_i(r).$

Another local-field model was presented by Lackner [198], who derived an expression which leads to an extension of Chynoweth's law,

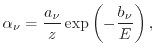$\displaystyle \ensuremath{\alpha _\nu}= \frac{a_\nu}{z} \exp \left( - \frac{b_\nu}{E} \right) ,$ (5.15)

including the field correction term

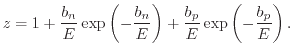$\displaystyle z = 1 + \frac{b_n}{E} \exp \left( - \frac{b_n}{E} \right) + \frac{b_p}{E} \exp \left( - \frac{b_p}{E} \right).$ (5.16)

The parameters $ a_\nu$ and $ b_\nu$ are described using the mean free carrier paths and the critical threshold energy which are not solely fitting parameters.

Slotboom et al. [199] have observed lower impact ionization rates for currents near the surface. As a consequence, models describing the transition between surface and bulk impact ionization have been developed [200]. However, Monte Carlo simulations have shown that there are no or only minor differences between surface and bulk impact ionization rates [201]. This means that there is no physical evidence of different rates near the surface and that those models are based on artifacts resulting from the approximate ionization rates based on the electric field.

In many applications, local-field based models deliver good results. However, from the physical point of view, impact-ionization is not field dependent. This is especially important in areas of rapidly changing electric fields and in small devices. This weakness can be observed in Fig. 5.4 for a 200nm and a 50nm structure. This figure compares generation rates calculated using different transport schemes. In this example, the electrons are accelerated from left to right. As soon as the electric field is risen, the local-field model predicts the carrier generation rate. However, physically more correct are the Monte Carlo reference simulations. They demonstrate that the carrier energy can follow changes in the electric field with a certain delay. At characteristic lengths shown in that figure, the validity of the local-field approach becomes questionable.

As long as device expansions are well above $ 200 $ nm, the advantages of local-field models are the good integrability in drift-diffusion schemes which are the workhorse in device simulation tools. Most TCAD simulators therefore commonly include one or more of the local electric field models. A typical application where drift-diffusion models deliver good results are high-voltage LDMOS transistors. Fig. 5.5 shows some results based on (5.13) and also clearly shows the importance of this physical effect. A more comprehensive example incorporating breakdown and snap-back simulations is presented in Section 5.3.

5.2.2 Non-Local Extensions to Local Field Models

Local modeling approaches do not provide information about where carriers come from and if they have already gained high energy. But since electrons and holes have to be accelerated to gain at least the threshold energy before impact-ionization can occur, this information is relevant. The area where there is a high electric field but impact-ionization has not started yet is often called dark-space [202]. This dark-space has to be considered also in experimental extractions of the ionization coefficients. Measuring of the coefficients cannot be performed directly. Therefore, they are commonly extracted out of the multiplication factor using the ionization integral (5.10). While considering the dark-space, the boundaries of the ionization integral are shifted so that only regions where impact-ionization takes place are included. With this approximation Okuto and Crowell [202] could explain anomalous energies which were found previously for the parameters $ E_r,$ $ E_i,$ and $ \lambda $ in (5.14). They have obtained more realistic energies employing a pseudo-local approximation which is also valid for high fields. In their work, a model using apparent and real ionization coefficients was developed. This technique delivered reasonable results for the given one-dimensional examples.

An interesting approach which includes local changes of the electric field is the method presented by Slotboom et al. [179] (compare (4.23)). The required post-processing which is necessary after a conventional drift-diffusion simulation, makes this method elaborative to implement, especially if self-consistent solutions are required.

5.2.3 Lucky Electron Model

The lucky electron concept [192,203] introduces a threshold energy level $ \ensuremath{\mathcal{E}}_\mathrm{II}.$ The carriers need to surmount this potential barrier in order to trigger impact-ionization. Hu et al. [203] describes that this energy can be reached if a carrier travels a sufficiently long distance without collisions. In this work by Hu, a compact model is formulated, which relates the substrate current $ \ensuremath{I_{\mathrm{Sub}}}$ as a consequence of impact-ionization with the drain current $ \ensuremath{I_\mathrm{D}}$ and the maximum electric field $ \ensuremath{E_{\mathrm{max}}}$ in the device. The drain current acts as a source function (the supply of carriers) and the peak field is used together with the (hot-carrier) mean free path $ \lambda $ to describe the ionization probability. This leads to

$\displaystyle \ensuremath{I_{\mathrm{Sub}}}= C_1 \ensuremath{I_\mathrm{D}}\exp ... ...rm{II}}}{\ensuremath{\mathrm{q}}\ensuremath{E_{\mathrm{max}}}\lambda} \right) ,$ (5.17)

where the derivation is based on the ionization rate similar to the definition in (5.13) [204].

A method to utilize the lucky electron model in device simulation and to introduce the non-locality has been proposed by Meinerzhagen [205]. In this work, the electric field line is followed starting from a point $ P$ until the electrostatic potential difference of $ V_B=\ensuremath{\mathcal{E}}_\mathrm{II} / \ensuremath{\mathrm{q}}$ has been reached at a point $ P_n.$ The length along the field line between $ P$ and $ P_n$ is $ d.$ The generation rate in the point $ P$ yields

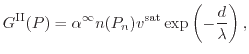$\displaystyle \ensuremath{G^{\mathrm{II}}}(P) = \ensuremath{\alpha ^{\infty}}n(P_n) \ensuremath{v^\mathrm{sat}}\exp \left( - \frac{d}{\lambda} \right) ,$ (5.18)

where $ n(P_n),$ $ \ensuremath{v^\mathrm{sat}},$ and $ \ensuremath{\alpha ^{\infty}}$ are the electron concentration in point $ P_n,$ the saturation velocity, and measured value from [189] to calibrate the results.

5.2.4 Carrier Temperature Based Modeling

Another approach for modeling impact-ionization employs the carrier temperature, i.e. the local mean carrier energy, as the key parameter. The formalism for the rate calculation is very similar to the local-field model. For the transformation of the commonly used local field based models, the electric field can be replaced by the homogenous stationary energy balance equation, compare (4.19), to form $ E=E(T_\nu, T_{\mathrm{L}})$ [206]. Thus, Chynoweth's law can be transformed from (5.13) to a carrier temperature dependent model. An often used estimation combining all coefficients reads [207]

$\displaystyle \ensuremath{\alpha _\nu}= \ensuremath{\alpha ^{\infty}}_\nu \exp ... ...emath{\mathcal{E}}^\mathrm{crit}_\nu}{\ensuremath{\mathrm{k_B}}T_\nu} \right) .$ (5.19)

The values $ \ensuremath{\alpha ^{\infty}}_\nu$ and $ \ensuremath{\mathcal{E}}^\mathrm{crit}_\nu$ are the high carrier temperature value of the ionization rate and the reference energy, respectively. Although these quantities have certain physical meanings, commonly they are used as fitting parameters.

Figure 5.4: Impact-ionization rates in two comparable n$ ^+$ -n-n$ ^+$ structures with a channel length of 200 nm (a) and 50 nm (b) (data from [186]). The local-field approach is calculated using Chynoweth's law (5.13) and the local energy approach using (5.19). The lateral shift of both approximations in comparison to the Monte Carlo can be seen. The smaller device, the more sever this gets. Also the typical overestimation using the local energy can be observed. The six moments method can reproduce the Monte Carlo data very well.
\includegraphics[width=0.51\textwidth]{figures/GII200_html.eps}
(a)

\includegraphics[width=0.51\textwidth]{figures/GII50.eps}
(b)

Figure 5.5: Distribution of the impact-ionization generation rate in the sample device with a drain voltage of 40 V and a gate voltage of 2 V (a). Influence of impact-ionization on the output characteristic using the LDMOS transistor from Chapter 4 (b).
\includegraphics[width=0.48\textwidth]{figures/II.eps}
(a) Impact-Ionization in the Device

\includegraphics[width=0.49\textwidth]{figures/output_II.eps}
(b) Breakdown

It seems natural to use the carrier energy in place of the electric field to model the impact-ionization rate and it is commonly used in the energy-transport or hydrodynamic simulation frameworks. Hence, it is possible to approximately consider non-local issues like the dark-space phenomenon. However, the carrier temperature alone cannot reflect the existence and strength of high-energy tails, i.e. the amount of high energetic carriers available. Completely different shapes of the distribution function can lead to the same average energy [15]. Additionally, high-energy tails can also exist if the average energies are low (compare Fig. 4.2 and 4.12). Therefore, the carrier temperature is commonly overestimated in small devices, which also leads to an overestimation of the impact-ionization rate [208,186]. These effects, which are especially relevant for aggressively down-scaled devices, can only be considered by incorporating the full distribution function.

5.2.5 Distribution Function Based Modeling

Instead of using the electric field, the carrier temperature, hot-carrier sub-populations, or some non-local approximations, the most rigorous modeling approach is to directly incorporate the carrier distribution function $ f(\ensuremath{\mathcal{E}}).$ This allows one to calculate the total generation rate using [187]

$\displaystyle \ensuremath{G^{\mathrm{II}}}= \int_{\ensuremath{\ensuremath{\math... ... g(\ensuremath{\mathcal{E}}) \ensuremath{ \mathrm{d}}\ensuremath{\mathcal{E}}.$ (5.20)

Here, the threshold energy is described using the symbol $ \ensuremath{\mathcal{E}}_\mathrm{th}$ , $ g(\ensuremath{\mathcal{E}})$ is the density of states, and $ P_\mathrm{II}(\ensuremath{\mathcal{E}})$ the ionization probability. This probability is often represented by the Keldysh [209] approach

$\displaystyle P_\mathrm{II}(\ensuremath{\mathcal{E}}) = P_0 \left( \frac{\ensur... ...}}_\mathrm{th}}}{\ensuremath{\ensuremath{\mathcal{E}}_\mathrm{th}}} \right)^2 ,$ (5.21)

or the approach presented by Kamakura [210]

$\displaystyle P_\mathrm{II}(\ensuremath{\mathcal{E}}) = P_0 \left( \ensuremath{... ...6, \quad \ensuremath{\mathcal{E}}_\mathrm{th}=1.1\ensuremath{ {\mathrm{eV}}} .$ (5.22)

The integration boundaries in (5.20) show that only carriers above a certain energy threshold $ \ensuremath{\ensuremath{\mathcal{E}}_\mathrm{th}}$ influence the generation rate and highlight that high energies are of vital importance. Approximations of the distribution function based on splitting hot and cold carrier fractions (as shown in (4.32) for the six moments model [134]) provide results in good agreement with the more precise but also very time-consuming full-band Monte Carlo method (see Fig. 5.4).


5.2.6 Energy Driven Paradigm

In the work of Rauch and La Rosa [211,212], a compact modeling approach for the total substrate current is presented. Although this compact model cannot be used for TCAD, it highlights the importance of the shape of the distribution function. Here, the substrate current of an n-MOSFET is formulated as

$\displaystyle \frac{\ensuremath{I_{\mathrm{Sub}}}}{\ensuremath{I_\mathrm{D}}} \... ..._c(\ensuremath{\mathcal{E}}) \ensuremath{ \mathrm{d}}\ensuremath{\mathcal{E}},$ (5.23)

where $ f_c(\ensuremath{\mathcal{E}})$ is the carrier energy distribution function and $ P_\mathrm{II}$ stands for the impact-ionization cross section [211]. The function of the source current $ F(\ensuremath{I_{\mathrm{S}}})$ enters either linearly as $ F(\ensuremath{I_{\mathrm{S}}})=\ensuremath{I_{\mathrm{S}}}$ or quadratically as $ F(\ensuremath{I_{\mathrm{S}}})=\ensuremath{I_{\mathrm{S}}}^2,$ depending on the importance of electron-electron scattering[213,214]. The authors suggest that there are commonly one or more dominant energies ( $ \ensuremath{\mathrm{q}}\ensuremath{V_{\mathrm{eff}}}^i$ ) at which the integrand of (5.23) peaks and one can approximate the integral as

$\displaystyle \int P_\mathrm{II}(\ensuremath{\mathcal{E}}) f_c(\ensuremath{\mat... ...\mathrm{eff}}}^i) f_c(\ensuremath{\mathrm{q}}\ensuremath{V_{\mathrm{eff}}}^i) .$ (5.24)

The dominant energies can be extracted by comparing the slopes of $ P_\mathrm{II}(\ensuremath{\mathcal{E}})$ and $ f_c(\ensuremath{\mathcal{E}})$ in logarithmic scale. The knee energies correspond to the maximum of the integrand in (5.23). This corresponds to the position where the multipliers have the same steepness but one is decaying (the distribution function) while the other one is increasing (the probability). Mathematically, this gives

$\displaystyle \frac{\ensuremath{ \mathrm{d}}\ln f_C}{\ensuremath{ \mathrm{d}}... ...thrm{d}}\ln P_\mathrm{II}}{\ensuremath{ \mathrm{d}}\ensuremath{\mathcal{E}}} ,$ (5.25)

and commonly coincides with knee points of $ f(\ensuremath{\mathcal{E}})$ or $ P_\mathrm{II}(\ensuremath{\mathcal{E}}).$ For $ P_\mathrm{II}$ the Kamakura relation (5.22) is assumed, with $ \ensuremath{\mathcal{E}}_\mathrm{th}$ being the band-gap energy $ \ensuremath{\mathcal{E}}_g.$ In long channel devices $ f_C(\ensuremath{\mathcal{E}})$ can be described using the heated Maxwellian distribution function as $ f_C(\ensuremath{\mathcal{E}}) \propto \exp (-\ensuremath{\mathcal{E}}/ \ensuremath{\mathrm{q}}\lambda\ensuremath{E_{\mathrm{max}}}).$ $ f_C$ has no knee and the slope is controlled by the maximum electric field ( $ -1/\ensuremath{\mathrm{q}}\lambda\ensuremath{E_{\mathrm{max}}}$ ).

As shown in Fig. 5.6(a) the maximum of the integrand depends on the slope of the carrier energy distribution and results according to (5.25) in

$\displaystyle \ensuremath{\mathrm{q}}\ensuremath{V_{\mathrm{eff}}}= \ensuremath{\mathcal{E}}_g + p \ensuremath{\mathrm{q}}\lambda \ensuremath{E_{\mathrm{max}}}.$ (5.26)

Due to the dependence of $ \ensuremath {\mathrm {q}}\ensuremath {V_{\mathrm {eff}}}$ on the maximum electric field, Rauch et al. call this relation the field driven approximation. By inserting this result in (5.23) one obtains

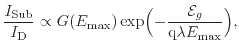$\displaystyle \frac{\ensuremath{I_{\mathrm{Sub}}}}{\ensuremath{I_\mathrm{D}}} \... ...l{E}}_g}{\ensuremath{\mathrm{q}}\lambda \ensuremath{E_{\mathrm{max}}}} \Bigr) ,$ (5.27)

where $ G(\ensuremath{E_{\mathrm{max}}})$ summarizes the remaining components which are not evaluated explicitly. This result corresponds to the lucky electron model (5.17).

In down-scaled devices the carrier energy distribution exhibits a knee near the maximum energy available from the steep potential drop along the pinch off region which is approximated as $ \ensuremath{V_{\mathrm{DS}}}-\ensuremath{V_{\mathrm{D,sat}}}$ [211]. Due to the constantly rising scattering rate and the abrupt decrease of the carrier distribution function near the knee point the maximum of the integrand in (5.23) at $ \ensuremath{\mathrm{q}}\ensuremath{V_{\mathrm{eff}}}^i$ coincides with the knee near (see Fig. 5.6(b))

$\displaystyle \ensuremath{V_{\mathrm{eff}}}\approx \ensuremath{V_{\mathrm{DD}}}- \ensuremath{V_{\mathrm{D,sat}}}.$ (5.28)

In this case the dominant energy is determined by the knee of the distribution function, which by itself depends on the bias conditions and therefore on the available energy [215]. Further influences of voltage changes seam not to shift this peak level. Hence, the final rate is proposed to be

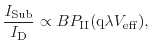$\displaystyle \frac{\ensuremath{I_{\mathrm{Sub}}}}{\ensuremath{I_\mathrm{D}}} \... ...B P_\mathrm{II}(\ensuremath{\mathrm{q}}\lambda \ensuremath{V_{\mathrm{eff}}}) ,$ (5.29)

where $ B$ includes that part of (5.23) which is not explicitly evaluated.

Figure 5.6: Schematic representation of the field (a) and energy driven (b) paradigms by Rauch and La Rosa. In the field driven paradigm a heated Maxwellian distribution is assumed with the carrier energy defined by $ \mathrm {q} \lambda E_\mathrm {max}.$ The maximum of the integrand is therefore found at the energy $ \mathrm {q} V_\mathrm {eff}$ and can be evaluated using $ E_\mathrm {max}$ as given in (5.24). In the energy driven paradigm $ V_\mathrm {eff}$ is controlled by the knee of the energy distribution function estimated according to (5.28).
\includegraphics[height=69mm]{figures/ii_rauch_field}
(a) Field-Driven

\includegraphics[height=69mm]{figures/ii_rauch_energy}
(b) Energy-Driven

This particular idea of this compact model is to combine the two regimes in one model. It herby highlights the necessity of new modeling paradigms when proceeding to small, down-scaled devices. The validity of both regimes has been shown in [211].

next up previous contents
Next: 5.3 Case Study: Simulation Up: 5. Impact-Ionization Generation Previous: 5.1 Basics of Impact-Ionization
O. Triebl: Reliability Issues in High-Voltage Semiconductor Devices