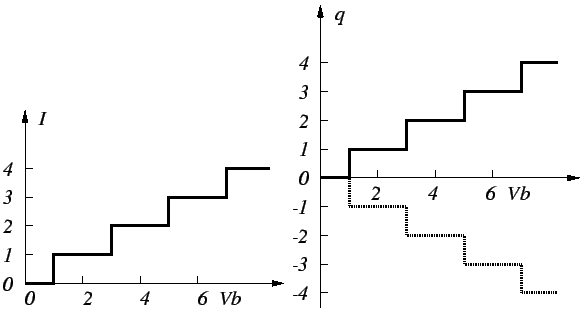Next: 2.8 Single Electron Transistor
Up: 2 Theory of Single
Previous: 2.6 Influence of the
2.7 The Double Tunnel Junction
Consider two tunnel junctions in series biased with an ideal voltage
source as shown in Fig. 2.7.
The charges on junction one, junction two, and on the whole island can be
written as
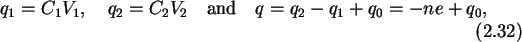
respectively, with n1 the number of electrons that tunneled through the
first junction entering the island, n2 the number of electrons that tunneled
through the second junction exiting the island, and n=n1-n2 the net number
of electrons on the island.
Figure 2.7:
Two tunnel junctions in series biased with an ideal voltage source.
The background charge q0 is non-integer, and n1 and n2 denote the
number of tunneled electrons through junction one and junction two,
respectively.
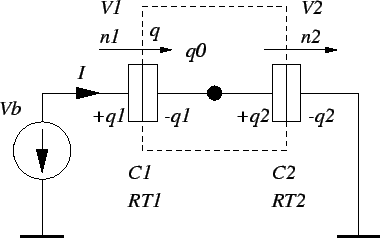 |
A background charge
q0 produces generally a
non-integer charge offset. The background charge is induced by
stray capacitances that are
not shown in the circuit diagram
Fig. 2.7 and impurities located near the
island, which
are practically always present. Using (2.32) and
Vb=V1+V2gives
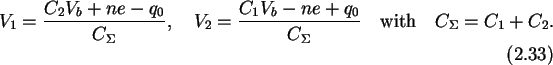
With (2.33) the
electrostatic energy
stored in the double junction is
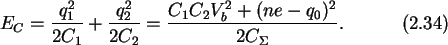
In addition, to get the free energy one must consider, as in
(2.11), the work done by the voltage source. If one electron
tunnels through the first junction the voltage source has to replace this
electron -e, plus the change in
polarization charge
caused by the tunneling
electron.
V1 changes according to (2.33) by
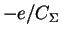 and hence
the polarization charge is
and hence
the polarization charge is
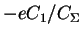 .
The charge q1 gets smaller,
which means that the voltage source `receives' polarization charge.
The total charge that has to be replaced by the voltage source is therefore
.
The charge q1 gets smaller,
which means that the voltage source `receives' polarization charge.
The total charge that has to be replaced by the voltage source is therefore
 and the work done by the voltage source in case electrons
tunnel through junction one and junction two is accordingly
and the work done by the voltage source in case electrons
tunnel through junction one and junction two is accordingly
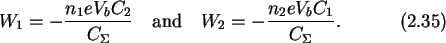
The
free energy of the complete
circuit is
At zero temperature, the system has to evolve from a state of higher energy
to one of lower energy. At non-zero temperatures transitions to higher energy
states are possible, but have exponentially reduced probability (see
2.23). The change in free
energy for an electron tunneling through junction one and two is given by
The probability of a tunnel event will only be high, if the change in free
energy is negative - a transition to a lower energy state. This is a direct
consequence of (2.23). The leading term in
(2.37) and
(2.38) causes  to be positive until the
magnitude of the bias voltage Vb exceeds a threshold which depends on the
smaller of the two capacitances. This is the case for all possible transitions
starting from an uncharged island, n=0 and q0=0.
For symmetric junctions (C1 = C2) the condition
becomes
to be positive until the
magnitude of the bias voltage Vb exceeds a threshold which depends on the
smaller of the two capacitances. This is the case for all possible transitions
starting from an uncharged island, n=0 and q0=0.
For symmetric junctions (C1 = C2) the condition
becomes
 .
This suppression of tunneling for low bias
is the Coulomb blockade. The Coulomb blockade can be visualized with an
energy diagram
Fig. 2.8.
.
This suppression of tunneling for low bias
is the Coulomb blockade. The Coulomb blockade can be visualized with an
energy diagram
Fig. 2.8.
Figure 2.8:
Energy diagram of a double tunnel junction without and with applied
bias. The Coulomb blockade causes an energy gap where no electrons can tunnel through
either junction. A bias larger than e/C overcomes the energy
gap.
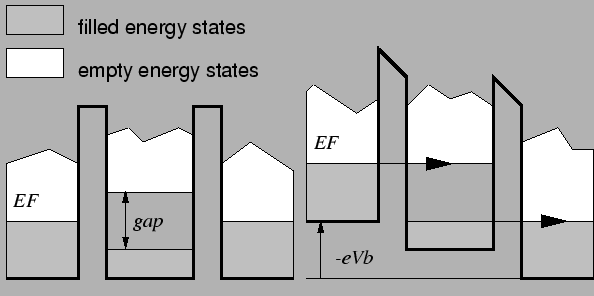 |
Due to the charging energy of the island, a Coulomb gap has
opened, half of which
appears above and half below the original Fermi energy. No electrons can
tunnel into the island from the left or right electrode, or out of the
island. Only if the bias voltage is raised above a threshold can electrons
tunnel in and out, and current will flow.
The same fact, the existence of a Coulomb blockade, is clearly visible in the
IV-characteristic,
Fig. 2.9.
Figure 2.9:
IV-characteristic of a double tunnel junction. The solid line
gives the characteristic for q0=0 and the dashed line for q0=0.5e.
The Coulomb blockade is
a direct result of the additional Coulomb energy, e2/2C, which must
be expended by an electron in order to tunnel into or out of the island.
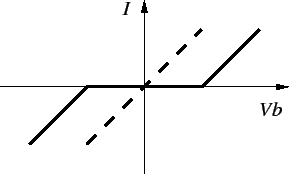 |
For low bias no current flows. As soon as Vb exceeds the threshold the
junction behaves like a resistor.
However, the background
charge q0 can reduce, or for
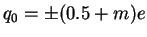 even eliminate the Coulomb blockade. This suppression
of the Coulomb blockade due to virtually uncontrollable background charges is one of
the major problems of single-electron devices. It will be addressed in more detail in
Section 5.2.3.
even eliminate the Coulomb blockade. This suppression
of the Coulomb blockade due to virtually uncontrollable background charges is one of
the major problems of single-electron devices. It will be addressed in more detail in
Section 5.2.3.
If an electron enters the island via junction one, it is energetically
highly favorable for another electron to tunnel through junction two out of
the island. Thus an electron will almost immediately exit the island
after the first electron entered the island.
This is a
space-correlated tunneling of electrons
(see Fig. 2.10).
After a varying duration another electron might first exit the island via
junction two and again, immediately a new electron will
tunnel through
junction one, entering the island and establishing charge neutrality on the
island. If the
transparency of the tunnel junctions is strongly different, for example
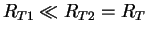 ,
a staircase like
IV-characteristic appears,
as shown in Fig. 2.11.
,
a staircase like
IV-characteristic appears,
as shown in Fig. 2.11.
Figure 2.10:
Space-correlation of tunneling in a double tunnel junction. A
tunnel event in junction one is immediately followed by an event in
junction two and vice versa. The duration between those tunnel pairs is
varying.
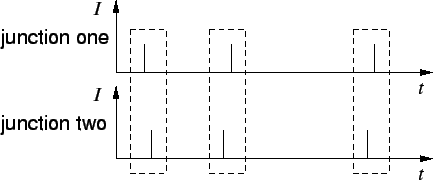 |
Figure 2.11:
For strongly differing tunnel junctions a staircase like
IV-characteristic appears. Depending on which tunnel junction is more
transparent, and the direction in which the charge carriers flow, the island
will be populated or depleted by an integer number of carriers with
increasing bias voltage. If carriers enter the island through the more
transparent junction and leave through the opaque one the island will
be populated with excess carriers. If they have to enter through the
opaque junction and leave through the transparent one, the island is
depleted of carriers.
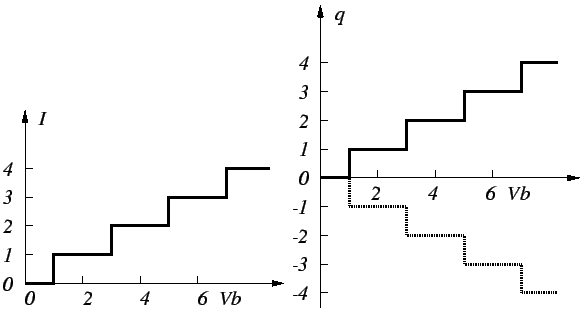 |
Carriers enter the island through the first tunnel junction and are
kept from the high resistance of the second junction from immediately
leaving it. Finally the carrier will, due to the high bias, tunnel out
of the island, which quickly triggers another electron to enter through
junction one. For most of the time the island is charged with one
excess elementary charge. If the bias is increased more
electrons will most of the time populate the island. The charge
characteristic is shown on the right side of Fig. 2.11.
If the asymmetry is turned around and
the second junction is more transparent
then the first one,
 ,
the island will be
de-populated and the charge on the island shows a descending staircase
characteristic. Carriers are sucked away from the island through the
transparent junction and can not be replenished quickly enough
through the opaque one. However, the IV-characteristic does
not change.
,
the island will be
de-populated and the charge on the island shows a descending staircase
characteristic. Carriers are sucked away from the island through the
transparent junction and can not be replenished quickly enough
through the opaque one. However, the IV-characteristic does
not change.




Next: 2.8 Single Electron Transistor
Up: 2 Theory of Single
Previous: 2.6 Influence of the
Christoph Wasshuber
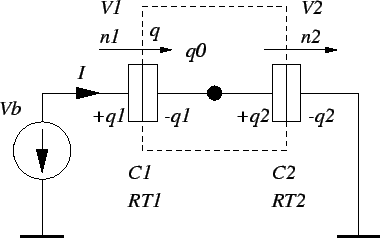
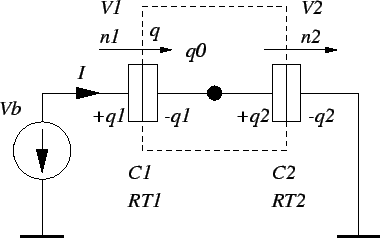
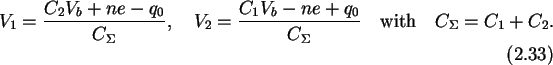
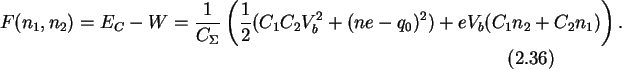
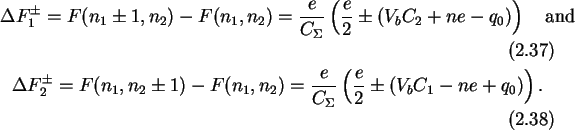


![]() even eliminate the Coulomb blockade. This suppression
of the Coulomb blockade due to virtually uncontrollable background charges is one of
the major problems of single-electron devices. It will be addressed in more detail in
Section 5.2.3.
even eliminate the Coulomb blockade. This suppression
of the Coulomb blockade due to virtually uncontrollable background charges is one of
the major problems of single-electron devices. It will be addressed in more detail in
Section 5.2.3.
![]() ,
a staircase like
IV-characteristic appears,
as shown in Fig. 2.11.
,
a staircase like
IV-characteristic appears,
as shown in Fig. 2.11.