



Next: 5.2.3 Random Background Charge
Up: 5.2.2 Error Rate/Probability
Previous: Bit Errors
Due to the stochastic nature of the tunnel process, the exact tunnel time of an
electron is not known. One only knows rates and probabilities, which results
in the need to wait considerably longer than the actual charging process
would take, to assure with a certain error probability, that an electron
actually tunneled. From (2.23) it follows that the
tunnel rate will be of the magnitude
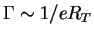 .
Thus, the average
tunnel time is
.
Thus, the average
tunnel time is
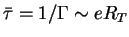 .
With a typical tunnel
resistance of
.
With a typical tunnel
resistance of
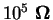 the average tunnel time
becomes
the average tunnel time
becomes
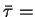 0.02 ps.
If one assumes that a tera-bit (1012) chip is written or read every
second for three years (108 s) and one permits in average only
one error, one needs an error probability for reading and writing of
0.02 ps.
If one assumes that a tera-bit (1012) chip is written or read every
second for three years (108 s) and one permits in average only
one error, one needs an error probability for reading and writing of
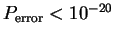 .
Assuming an exponential distribution of the tunnel time
(3.28) of an electron gives
.
Assuming an exponential distribution of the tunnel time
(3.28) of an electron gives
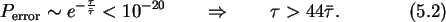
Therefore one must wait about 1 ps for an electron to tunnel with
an error rate lower than 10-20. One picosecond would still be a
very good access time. But the values used for this estimation can easily
vary by a factor ten or even hundred. For instance, a tunnel resistance
of 1 M
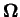 is a common value. This would raise the estimated
value to 10 ps. Equally, the assumption of a free energy drop
of 1 eV, which was used for the rate estimation
is a common value. This would raise the estimated
value to 10 ps. Equally, the assumption of a free energy drop
of 1 eV, which was used for the rate estimation
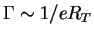 ,
for the
tunnel event might not be reached. A smaller change in free energy reduces
the tunnel rate and prolongs the average tunnel time.
,
for the
tunnel event might not be reached. A smaller change in free energy reduces
the tunnel rate and prolongs the average tunnel time.




Next: 5.2.3 Random Background Charge
Up: 5.2.2 Error Rate/Probability
Previous: Bit Errors
Christoph Wasshuber