Characterization of electrically active defects at III-N/dielectric interfaces

 
« PreviousUpNext »Contents
Previous: 4 Modeling of charge trapping phenomena    Top: 4 Modeling of charge trapping phenomena    Next: 4.3 Extraction of the activation energy and from experimental data

4.2 The non–radiative multiphonon (NMP) model

A model capable of describing the physical mechanisms of charge exchange cannot ignore the structural deformation at the defect site. In fact, after an electron (or hole) is captured (or emitted) the microscopic configuration of the defect and the surrounding area changes into a different arrangement. Bond lengths and angles are adjusted in order to accommodate the captured (or missing) charge. In other words, the whole system relaxes towards its new equilibrium position, which is defined by the total potential energy of the system in the respective charge state. The total potential energy is often approximated by a harmonic potential. The equilibrium configuration is therefore defined by a certain equilibrium position \( q^0 \) (representing the mass–weighted coordinates of the defect site) and a certain equilibrium energy \( E^0 \), corresponding to the minimum of the harmonic potential. This is illustrated in Fig. 4.2.

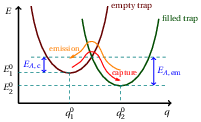
Figure 4.2: The potential energy of a defect site is approximated by a harmonic potential, which takes different equilibrium positions \( q^0 \) depending on its charge state. A charge exchange event is therefore a transition between the two potential energy surfaces. In the classical limit, a non–radiative, multiphonon transition must occur through their crossing point, as shown by the arrows.

When a trapping (or detrapping) event takes place, the equilibrium position and the energy of the system change. In this way, the transition from the initial state in \( q^0_1 \) to the final state in \( q^0_2 \) requires a transition between two potential energy surfaces. Without any external electromagnetic excitation, in a classical, high temperature approximation this can happen only through the crossing point of the two potential energy functions. In this way, an energy barrier is associated with each charge trapping event. The excess energy, called activation energy \( E_A \), is provided to the system as thermal energy through phonon scattering. A non–radiative multiphonon (NMP) transition [76–78] is therefore a thermally activated process, which can be described in the classical high–temperature limit by the Arrhenius equation

(4.3) \begin{equation} \tau = \tau _0 \; \mr {e}^{E_A / k_\mr {B} \mr {T}}. \label {arrh} \end{equation}

We note the similarity of Eq. (4.3) with Eq. (4.2), if we assume \( \tau _0^{-1} = N_\mr {C} \, v_{\mr {th}} \, \sigma \) (or \( \tau _0^{-1} = N_\mr {V} \, v_{\mr {th}} \, \sigma \)). The difference is the physical meaning of the energetic barrier: in the SRH picture, it is defined by the energetic position of the trap with respect to the reservoir; for the NMP model it must be determined from the shape and position of the potential energy functions of the initial and final defect configurations.

The temperature dependence of a charge trapping event is given by the Boltzmann factor in the Arrhenius equation, while the applied bias has an influence on the activation energy. In fact, a modification to the gate voltage results in an offset for one of the two potential energy surfaces, thereby changing their relative positions and thus causing a different \( E_A \).

With such a picture of the trapping mechanism we are able to explain very complex charge trapping dynamics, which would not be possible with the model presented in the previous section. For example, the physical model based on NMP transition can explain complex CET maps, allowing a defect to have a short time constant for capture but a long one for emission, because it is possible to find a state with a low barrier energy for capture and a large one for emission processes [79]. In fact, some defects have similar capture and emission time constants and therefore can be charged and discharged continuously within stress and recovery cycles, resulting in a fully recoverable degradation. Other trap sites have emission times much longer than for capture, giving rise to an almost permanent voltage drift, which can eventually recover only after very long time, or with high temperature annealing processes. Furthermore, it was shown that the behavior of threshold voltage drifts of silicon MOSFETs under NBTI can be fully explained only introducing intermediate, metastable defect configurations between the empty trap equilibrium state \( q_\mr {e}^0 \) and the filled trap equilibrium state \( q_\mr {f}^0 \)  [80]. These states can be represented in our picture as local minima of the potential energy surfaces, with very similar energy values. The metastable states are also responsible for the anomalous random telegraph noise (RTN) observed in such structures  [27, 81].

The temperature dependence of Eq. (4.3) can be used for temperature acceleration [82, 83]. Each experimental dataset is conducted at constant temperature (isothermal measurements), and we expect the trap sites to contribute to the device drift in a different way at different temperatures. However, the time constants \( \tau _1 \) and \( \tau _2 \) of the same defect at temperature \( \mr {T_1} \) and \( \mr {T_2} \) are related to each other by

(4.4) \begin{equation} \tau _2 = \tau _0 \; \left ( \frac {\tau _1}{\tau _0} \right ) ^{\mr {T_1}/\mr {T_2}} \label {eq4.4} \end{equation}

where \( \tau _0 \) is the coefficient of the Arrhenius’ equation. Eq. (4.4) enables us to bring all measurements at different temperature on the same axis, by introducing the temperature–time variable

(4.5) \begin{equation} \vartheta (\mr {T}) = \tau _0 \; \left ( \frac {t}{\tau _0} \right ) ^{\mr {T_{ref}}/\mr {T}}. \label {eq_theta} \end{equation}

This means that a measurement at cold temperature in the time window between \( t_0 \) and \( t_f \) is equivalent to a measurement at higher temperature between \( t_0’<t_0 \) and \( t_f’<t_f \). In other words, temperature has the effect of accelerating both stress and recovery mechanisms. This allows us to fix our experimental time window, and investigate shorter time scales by using low temperatures, and longer time scales by increasing it. The shortest accessible time is therefore determined by two factors: the time resolution of the instrument and the coldest temperature achievable in our setup.

In the following, we examine three different scenarios of increasing complexity. The simplest case is to consider \( \tau _0 \) a constant parameter and \( E_A \) to be single–valued (Section 4.2.1). However, this approximation can be too rough to properly explain the experimental data. Therefore, we consider the possibility of a continuous distribution of activation energies in Section 4.2.2, and of a non constant \( \tau _0 \) in Section 4.2.3.

4.2.1 Constant \( \mathbf {\tau _0} \), single activation energy

In general, under certain bias conditions, every defect has different parameters \( \tau _0 \) and \( E_A \). However, in a first approximation we can consider the pre–factor \( \tau _0 \) to be constant. This has been proven to be accurate enough for NBTI investigations on silicon MOSFETs [83]. Furthermore, we can recognize “families” of states, or defects of the same type, that have approximately the same activation energy. For example, we can group in a “family” all defects that have the same microscopic configuration (due to a certain impurity), or the same origin (due to the vacancy of a certain element). In this way, the charge trapping mechanisms are described by Eq. (4.3) with a constant factor \( \tau _0 \) and one, or more in case there are more defect “families”, single–valued activation energies.

According to the Arrhenius equation, the time response of every single interface state follows an exponential function with characteristic time \( \tau \). Each defect type \( n \), with activation energy \( E_{A, n} \), gives rise to the time constant \( \tau _n \), and contributes to the total voltage shift of the device with the fraction \( \Delta \mr {V}_n \). Summing up over all contributions, and assuming that electrons are being trapped into defects during stress, the threshold voltage shift increases as

(4.6) \begin{equation} \Delta \mr {V_{th}^{\,stress}} (t) = \sum _n \Delta \mr {V}_n \; \mr {e}^{- t / \tau _{\mr {c}, n}} \label {deltavstress} \end{equation}

and then, after it reaches a maximum threshold voltage shift of \( \Delta \mr {V_{max}} \), recovers according to

(4.7) \begin{equation} \Delta \mr {V_{th}^{\,recovery}} (t) = \Delta \mr {V_{max}} \;-\; \sum _n \Delta \mr {V}_n \; \mr {e}^{- t / \tau _{\mr {e}, n}}. \label {deltavrec} \end{equation}

If the activation energies of the defect types are quite different, it is possible to distinguish each contribution directly by looking at the time evolution of the \( \Delta \mr {V_{th}} \) [18]. The various \( \tau _n \) and the respective \( E_{A, n} \) can be easily extracted from a fit to the data. In Section 4.3.1 we present a straightforward method to extract the activation energy from \( \Delta V (t) \) data measured at different temperatures.

4.2.2 Constant \( \pmb {\tau _0} \), distributed activation energy

Experimental evidence has shown that the single exponential model is normally not sufficient to explain the actual time evolution of \( \Delta V \). In fact, we should consider that the interface between two materials, especially in the case of an amorphous dielectric, is characterized by a certain amount of variability in the arrangement of the atoms. For this reason, also the defects exhibit a certain diversity in bond length and angles, thus resulting in a continuous interval of allowed activation energies rather than a precise, single value \( E_{A, n} \). For example, we can describe a defect “family” with a gaussian distribution of activation energies around a mean value \( \mu \), with a certain standard deviation \( \sigma \). As a consequence, capture and emission time constant will follow a log-normal distribution and an analytical expression for the device drift can be written as  [79]

(4.8) \begin{equation} \Delta V_\mr {str} (t)= \frac {\Delta V_\mr {max}}{2} \; \mr {erfc} \left ( -\, \frac {k_\mr {B} \mr {T} \ln {\left ( \frac {\vartheta _\mr {str} (t)}{\tau _0} \right )} - \mu }{\sqrt {2} \, \sigma } \right ) \label {errfunct_str} \end{equation}

for stress, and

(4.9) \begin{equation} \Delta V_\mr {rec} (t)= \frac {\Delta V_\mr {max}}{2} \; \mr {erfc} \left ( \frac {k_\mr {B} \mr {T} \ln {\left ( \frac {\vartheta _\mr {rec} (t)}{\tau _0} \right )} - \mu }{\sqrt {2} \, \sigma } \right ) \label {errfunct_rec} \end{equation}

for recovery, where \( \Delta V_\mr {max} \) is the voltage drift at saturation, achieved when all traps have been filled. This approach contributed to great advances in the understanding of the defects present at Si/SiO\( _2 \) interfaces and responsible for NBTI: here two main “families” of trap states with gaussian–distributed activation energies have been discovered  [27].

However, the problem of determining the relevant defect groups from the experimental data may be complex if we observe a large number of contributions with very close \( E_A \) values. This is exactly the case for standard GaN/AlGaN MIS–HEMTs, for which a logarithmic temporal evolution is observed  [47, 67]. In fact, a function \( y \propto \mr {log}(x) \) can be fitted only by a large number of exponential components of the kind \( \mr {exp}(-x/\tau _n) \). The fit of a dataset constituted by a finite number of points, \( M \), with a multi–exponential model with an unknown number \( N \) of exponential components is in fact an ill–posed problem  [84]. The system in this case is underdetermined: this means that a set of solutions exists, rather than a unique one. A regularization method is therefore necessary in order to find the solution. If no additional information about the system is known, different approaches can be used. For example, the Tikhonov regularization method  [84] solves the problem by adding a constraint given by a certain smoothing functional of the solution. The method of maximum entropy (MEM)  [85, 86] instead chooses the most noncommital solution, i.e., the one which makes the least assumption on the data, thus fulfilling the parsimony principle by maximizing the Shannon entropy  [87]. In our case, we can apply a method that has been developed for the investigation of chemical reactions involving distributed activation energies, which is described in Section 4.3.2.

4.2.3 Non–constant \( \pmb {\tau _0} \)

In the cases discussed until now, the pre–factor \( \tau _0 \) is assumed to be constant, to be determined as a parameter of the fit to the whole dataset of measurements taken at different temperatures. However, in certain cases this approximation can be too crude and might lead to an error in the determination of the activation energy values.

The physical meaning of \( \tau _0 \) for a single charge transfer reaction following Eq. (4.3) can be related to the phonon frequency, i.e., how many phonons per unit time are available to provide energy to overcome the energetic barrier. In fact, the fitted value of \( \tau _0 \) from investigations on silicon MOSFETs agrees with the inverse of the phonon frequency in silicon, which has been measured and can be estimated with DFT calculations to be on the order of 1013 Hz  [83].

The first reason for the failure of the constant \( \tau _0 \) approximation can be a large variety of defect types. In fact, each type would have a characteristic \( \tau _{0, n} \) for its charge exchange reaction, related to the attempt frequency in that particular case. Such \( \tau _{0, n} \) is already an approximated value, averaged over the entire “family” of similar defects, each of which has its own characteristic \( \tau _0 \). The overall effect on a macroscopic device, however, has a characteristic time constant given by the average over the \( \tau _{0, n} \) of all the active defects in those conditions. As a consequence, if measurements at different temperatures access different defect types, it is clear that a single \( \tau _0 \) cannot be found. For example, this can happen if some traps have a quite large time constant, becoming active only at high temperatures, but are not accessible at low temperatures. The whole dataset from low to high temperatures in this case cannot be fitted accurately with the same \( \tau _0 \). An experimental approach that allows to avoid this problem is the time–dependent defect spectroscopy (TDDS), developed and used for NBTI studies on Si/SiO\( _2 \) MOSFETs. It relies on the measurement of small–area devices, thus allowing to deal with only a handful of defects at a time  [80, 88, 89] and therefore to determine the properties of each trap state individually.

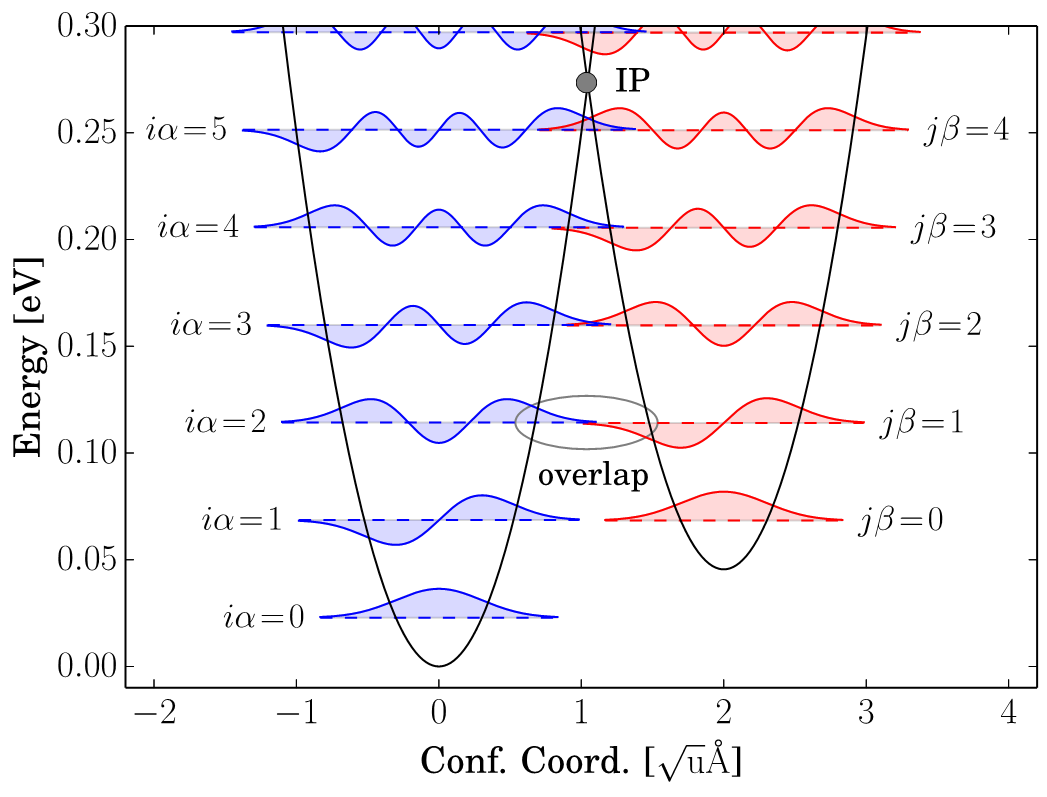
A second reason for a non–constant \( \tau _0 \) can be found in the inaccuracies arising from the classical approximation. In fact, Eq. (4.3) is based on the assumption that a transition between two potential energy functions occurs at the intersection point (IP), as illustrated in Fig. 4.3a. The IP determines the height of the barrier, that is the activation energy \( E_A \). However, the quantum–mechanical approach to the same problem possibly leads to a lower value for the energy barrier and a different \( \tau _0 \). The solutions of a harmonic potential are wavefunctions characterized by a discrete energy spectrum, as shown in Fig. 4.3a. 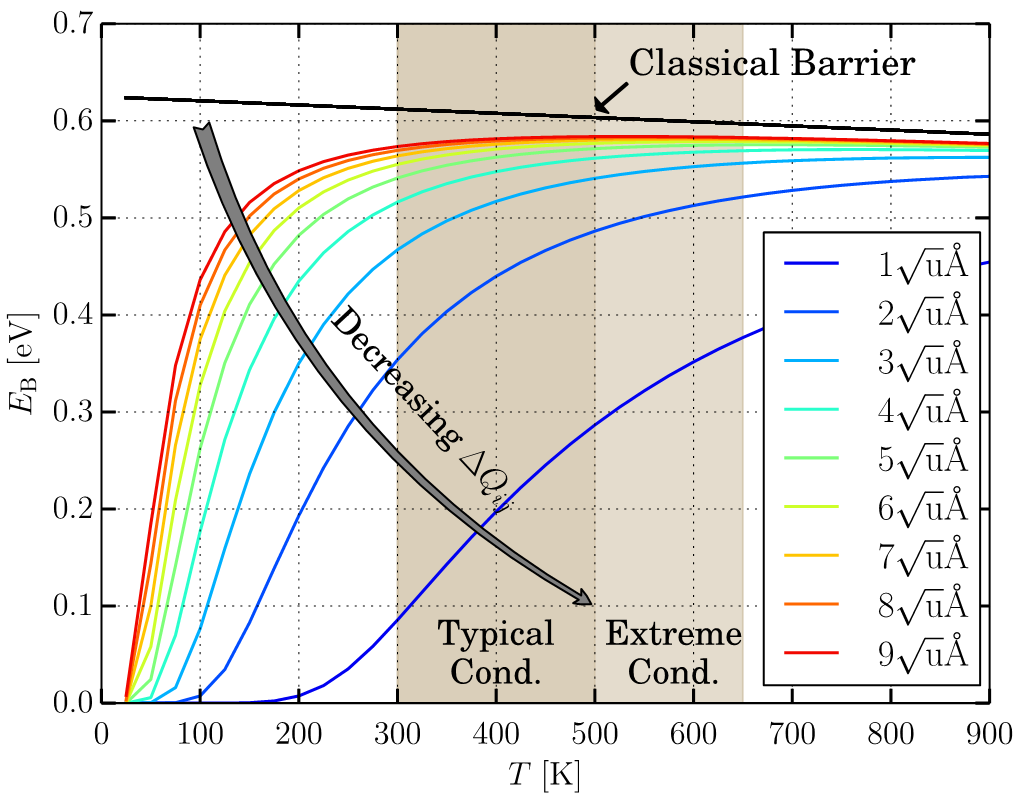Depending on the distance of the two equilibrium positions \( q^0_1 \) and \( q^0_2 \), it can happen that some excited states of the two harmonic potentials overlap at an energy below that of the IP. This gives a certain probability for the transition at a lower energy barrier than the classical one through carrier tunnelling. In Fig. 4.3b the activation energy in the classical limit and with the quantum–mechanical approach have been calculated as a function of temperature and for different values of displacement \( \Delta Q = q^0_2 - q^0_1 \)  [90], performing density functional theory (DFT) calculations based on the data obtained by TDDS studies on silicon MOSFETs. The error on \( E_A \) due to tunnelling is larger at cold temperatures, and it can be still relevant under typical conditions of device operation (down to 300 K). Unfortunately, at the present time it is not yet possible to perform the same calculations for GaN/AlGaN MIS–HEMTs, since the properties of the defects needed for DFT simulations are still unknown. Further investigations and the improvement of the characterization methods are therefore necessary to clarify this aspect.

(image)

Figure 4.3: The transition between two potential energy surfaces occurs at the intersection point (IP) in the classical approximation, but in the quantum–mechanical approach tunnelling between two wavefunctions can take place as well (a). The resulting activation energy can be much lower than the classical value (b), depending on temperature and the displacement \( \Delta Q \) between the two equilibrium coordinates (from  [90]).

In conclusion, if the wavefunction overlap is not negligible, the extraction of \( E_A \) and \( \tau _0 \) with Eq. (4.3) results in non–constant, temperature–dependent values: at higher temperature the energy would increase while \( \tau _0 \) would decrease. We discuss further the possible effects of a non–constant \( \tau _0 \) in Section 4.3.3.

« PreviousUpNext »Contents
Previous: 4 Modeling of charge trapping phenomena    Top: 4 Modeling of charge trapping phenomena    Next: 4.3 Extraction of the activation energy and from experimental data