


Next: 7. Summary and Conclusion
Up: Dissertation Robert Wittmann
Previous: 5. NBTI Reliability Analysis
Subsections
6. Applications
This chapter mainly presents three-dimensional simulation applications of ion
implantation processes for the investigation of dopant distributions in
topological complex targets. The strained or relaxed high-mobility materials
employed in the modeled device structures will likely be introduced in
leading-edge CMOS technology in the next several years. The simulation on
computers is advantageous over experimentally obtained doping profiles.
Firstly, it is faster and cheaper, and secondly, only one-dimensional doping
profiles can be measured by the SIMS technique. Two- and three-dimensional
simulation results provide a better insight into the implantation process than
an indirect measurement like measuring the electrical conductivity after some
process steps. The simulator MCIMPL-II has been ported to the operating system
AIX since the simulation of large three-dimensional device geometries requires
a huge amount of computer memory. Most of the three-dimensional applications
in this chapter were performed on an IBM-AIX p655 cluster with 64 Gigabyte of
main memory per node.
A special emphasis in the ion implantation applications is laid on the formation
of ultra-shallow junctions, since this topic is one of the most important issues
for processing heavily shrinked MOS devices. The simulation of low-energy
source/drain and extension implants is an attractive example to demonstrate
the simulation capabilities of a TCAD tool to analyze and optimize the resulting
dopant distribution in the device after multiple implantation steps by tuning
the process parameters of a single step. Furthermore, a three-dimensional
simulation treatment allows to study shadowing effects which arise for large
tilt-angle implantations by using self-aligned masking techniques. The most
prominent representative of this application class is the halo implantation
for punch-through suppression in advanced CMOS devices. However, an important
point is that the underlying implantation process is compatible with
contemporary CMOS process technology and it can be performed with existing
ion implantation equipment.
The NBTI reliability must be investigated under DC and AC stress conditions
for any high-performance CMOS technology that uses nitrided gate oxides.
The calibrated NBTI model described in Section 5 is used to study NBTI
degradation and lifetime for a full SRAM cell based on a 90nm technology.
In the performed simulation study, the impact of storing random bit values
on the NBTI lifetime of the memory cell is analyzed. We determine the lifetime
extension related to the DC lifetime of the cell as function of the
probability for storing a one bit between 100% and 50% every second.
The goal of the two presented three-dimensional simulation applications
is to evaluate the simulator in terms of functioning and performance.
A relatively simple structure is used in both implantation applications,
which represents a portion of an STI-isolated MOS device.
Downscaling of MOS transistors requires the formation of very shallow
source/drain junction depths which are estimated in Section 1.3 for
future CMOS technologies. It is expected that ion implantation technology
will continue to dominate the junction formation for advanced MOS devices.
Shallow n-type source/drain regions can be easily formed by low-energy arsenic
implantation supported by the rapid formation of a fully amorphous layer
during the implantation process caused by the high mass of arsenic ions and
high implantation doses.
Figure 6.1:
MOS structure (left) and mesh for the shallow arsenic
implant (right).
![\resizebox{1.1\linewidth}{!}{\rotatebox{0}{\includegraphics[clip]{figures/struct_as-comb}}}](img643.png)
|
Figure 6.2:
Shallow 5keV arsenic-implant distribution in the MOS structure.
![\resizebox{1.05\linewidth}{!}{\rotatebox{0}{\includegraphics[clip]{figures/shallow_as}}}](img644.png)
|
Figure 6.3:
Simulated shallow 5keV arsenic implant profile in
the substrate.
![\resizebox{1.0\linewidth}{!}{\rotatebox{0}{\includegraphics[clip]{figures/As_LAT-1D}}}](img645.png)
|
The input structure and the mesh for the arsenic implantation are shown in
Fig. 6.1, which has been generated in a similar manner as described
in the demonstration example in Section 3.2.5. The MOS structure has a base
area of
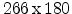 nm and consists of four segments including the
standard materials silicon, oxide, and polysilicon.
A scattering oxide layer with a thickness of 5nm is used on top of the silicon
substrate which is surrounded by STI isolation in the modeled structure.
The mesh for the projected shallow implant has 19478 mesh points and
101406 tetrahedral elements. An anisotropic mesh refinement has been applied
locally to optimize the mesh for the intended shallow doping and to keep the
overall grid below
nm and consists of four segments including the
standard materials silicon, oxide, and polysilicon.
A scattering oxide layer with a thickness of 5nm is used on top of the silicon
substrate which is surrounded by STI isolation in the modeled structure.
The mesh for the projected shallow implant has 19478 mesh points and
101406 tetrahedral elements. An anisotropic mesh refinement has been applied
locally to optimize the mesh for the intended shallow doping and to keep the
overall grid below 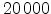 points. Arsenic ions have been implanted with an
energy of 5keV, a dose of
points. Arsenic ions have been implanted with an
energy of 5keV, a dose of
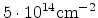 , and a tilt of
7
, and a tilt of
7 . The accurate Monte Carlo simulation with eight million ions resulted
in the three-dimensional arsenic distribution presented in Fig. 6.2.
The corresponding one-dimensional arsenic concentration profile in
Fig. 6.3 was obtained by only
. The accurate Monte Carlo simulation with eight million ions resulted
in the three-dimensional arsenic distribution presented in Fig. 6.2.
The corresponding one-dimensional arsenic concentration profile in
Fig. 6.3 was obtained by only
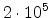 simulated ions.
The doping profile reaches its peak concentration of almost
simulated ions.
The doping profile reaches its peak concentration of almost
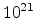 atoms/
atoms/
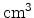 at a depth of 2nm below the surface of the
substrate and it is characterized by a steep rise and fall of the dopant
concentration around the maximum.
at a depth of 2nm below the surface of the
substrate and it is characterized by a steep rise and fall of the dopant
concentration around the maximum.
Figure 6.4:
MOS structure (left) and mesh for the deep boron
distribution (right).
![\resizebox{1.08\linewidth}{!}{\rotatebox{0}{\includegraphics[clip]{figures/struct_b}}}](img651.png) |
6.1.2 Large-Tilt-Angle Boron Implantation With Quad Repositioning
The LAT (large angle tilt) implantation technique can be employed
to achieve a larger lateral penetration of the dopants under a mask edge for
processing optimized device structures required for advanced CMOS applications.
This technique uses large tilt angles in combination with target wafer rotational
repositioning during the implant processing sequence, without removing the wafer
from the implant platen. The LAT implant technology is typically applied to form
the halo implants (or ``pocket'' implants) for the punch-through suppression in
shrinked MOS devices. A tilt of 30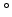 is used for the simulated sequence
of boron implantations which are performed by using a wafer rotation of 90
is used for the simulated sequence
of boron implantations which are performed by using a wafer rotation of 90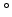 after each implantation step. The already used ``Manhatten'' structure is well
suited to demonstrate the equality of the obtained boron distributions between
the twist angles of 0
after each implantation step. The already used ``Manhatten'' structure is well
suited to demonstrate the equality of the obtained boron distributions between
the twist angles of 0
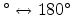 and the symmetry
between 90
and the symmetry
between 90
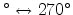 .
.
The structure and the generated mesh for the boron implantation are shown in
Fig. 6.4. The created volume mesh consists of 8228 mesh points and
41266 tetrahedral elements of similar size. The simulated boron distributions
are shown in Fig. 6.5, processed with an energy of 25keV, a dose of
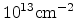 , and a tilt of 30
, and a tilt of 30 . The Monte Carlo
simulation was carried out with four million particles for each implantation
step. The simulation domain and the external implantation window were both
expanded by about 50nm perpendicular to the front, back, left, and right
boundaries of the input geometry to avoid any boundary influence for the
dopant distribution at the surface of the device structure.
. The Monte Carlo
simulation was carried out with four million particles for each implantation
step. The simulation domain and the external implantation window were both
expanded by about 50nm perpendicular to the front, back, left, and right
boundaries of the input geometry to avoid any boundary influence for the
dopant distribution at the surface of the device structure.
Figure 6.5:
Sequence of four 25keV boron LAT implants with
a tilt of 30 , processed by 90
, processed by 90 rotational repositioning of
the test structure.
rotational repositioning of
the test structure.
![\resizebox{1.089\linewidth}{!}{\rotatebox{0}{\includegraphics[clip]{figures/quadimpl_b}}}](img655.png) |
Fig. 6.5 demonstrates the successfully performed symmetry check
for the simulator MCIMPL-II. The three-dimensional results obtained at a
twist of 0 and 180
and 180 are evidently equal, while the results
at 90
are evidently equal, while the results
at 90 and 270
and 270 are mirror-symmetric to each other.
are mirror-symmetric to each other.
The boron LAT implants in the one-dimensional SiO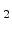 /Si layer structure
were simulated with
/Si layer structure
were simulated with
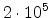 ion trajectories by using the same
implantation conditions as for the three-dimensional test structure.
Fig. 6.6 demonstrates that all four boron implantations yield the
same doping profile since the used ion beam directions are
crystallographically identical.
ion trajectories by using the same
implantation conditions as for the three-dimensional test structure.
Fig. 6.6 demonstrates that all four boron implantations yield the
same doping profile since the used ion beam directions are
crystallographically identical.
The formation of ultra-shallow source/drain and extension regions by two ion
implantation steps is demonstrated for a 65nm gate-length n-MOS transistor,
which is shown in Fig. 6.7. The modeled device structure has a 12nm
thick strained silicon channel layer on top of a 620nm thick relaxed
Si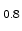 Ge
Ge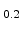 virtual substrate block with a base area of
virtual substrate block with a base area of
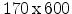 nm. The gate oxide has a thickness of 2nm and can be
grown by thermal oxidation of strained silicon. The simulated high-performance
n-MOS transistor is electrically isolated from other devices by using a
chip-area saving shallow trench isolation (STI). The MOS structure can be used
for processing strained silicon n- and p-MOSFETs depending on the implanted
dopant species. Using scaling considerations, a source/drain vertical junction
depth around 27.5nm is recommended by the ITRS roadmap for the fabrication of
a 65nm technology node, as shown in Table 1.1.
nm. The gate oxide has a thickness of 2nm and can be
grown by thermal oxidation of strained silicon. The simulated high-performance
n-MOS transistor is electrically isolated from other devices by using a
chip-area saving shallow trench isolation (STI). The MOS structure can be used
for processing strained silicon n- and p-MOSFETs depending on the implanted
dopant species. Using scaling considerations, a source/drain vertical junction
depth around 27.5nm is recommended by the ITRS roadmap for the fabrication of
a 65nm technology node, as shown in Table 1.1.
Figure 6.8:
Simulated three-dimensional dopant distribution in the
n-MOS structure after performing the 2keV arsenic source/drain extension implantation.
|
Figure 6.7:
Modeled structure of the half of a high-performance
strained-Si/Si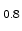 Ge Ge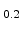 n-MOSFET with an STI isolation scheme. n-MOSFET with an STI isolation scheme.
![\resizebox{0.88\linewidth}{!}{\rotatebox{0}{\includegraphics[clip]{figures/str_struct}}}](img658.png)
|
|
Figure 6.10:
Final dopant distribution in the cross-section of the MOSFET
along the channel after performing the 6keV arsenic source/drain implantation.
|
Figure 6.9:
Top view of the meshed STI transistor structure
with sidewall spacer.
![\resizebox{0.94\linewidth}{!}{\rotatebox{0}{\includegraphics[clip]{figures/str_fullgrid}}}](img660.png)
|
|
Figure 6.11:
Final implanted source/drain doping profile
of the strained n-MOSFET along a vertical line through the drain region.
![\resizebox{1.0\linewidth}{!}{\rotatebox{0}{\includegraphics[clip]{figures/As_SSi_diss}}}](img662.png)
|
In the first ion implantation step, the arsenic source/drain extensions were
implanted with an energy of 2 keV and a dose of
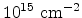 .
Fig. 6.8 shows the arsenic distribution in the device structure
without sidewall spacer after smoothing of the Monte Carlo result and
translating it to the destination mesh. For the ion implantation simulation
of the source/drain extensions, the nitride spacer segment is cut off from
the meshed transistor structure. Fig. 6.9 shows the meshed
structure required to simulate the second implantation step in the two-step
sequence. While no additional segments can be added to a final meshed device
structure, any non-required segment of the structure can be removed.
.
Fig. 6.8 shows the arsenic distribution in the device structure
without sidewall spacer after smoothing of the Monte Carlo result and
translating it to the destination mesh. For the ion implantation simulation
of the source/drain extensions, the nitride spacer segment is cut off from
the meshed transistor structure. Fig. 6.9 shows the meshed
structure required to simulate the second implantation step in the two-step
sequence. While no additional segments can be added to a final meshed device
structure, any non-required segment of the structure can be removed.
In the second arsenic implantation step, the source/drain regions are formed
using an energy of 6 keV and a dose of
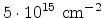 .
Fig. 6.10 shows the simulated cross-section along the channel of the
strained n-MOSFET after performing the source/drain implants. In this
application the Monte Carlo simulation was carried out with
.
Fig. 6.10 shows the simulated cross-section along the channel of the
strained n-MOSFET after performing the source/drain implants. In this
application the Monte Carlo simulation was carried out with
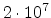 ion trajectories per implantation step to achieve a
low statistical fluctuation of the predicted doping profiles.
ion trajectories per implantation step to achieve a
low statistical fluctuation of the predicted doping profiles.
The use of multiple ion implantation steps with different energies and doses
allows to optimize the doping in the device for source/drain engineering
problems. Fig. 6.11 compares the simulated one-dimensional doping
profiles obtained after the first and after the second arsenic implantation
step. The superposition of both implanted dopant distributions produces two
peak concentrations in the final arsenic profile. The simulation analysis of
a specific ion implantation sequence is very useful to determine the exact
process parameters required for a desired doping profile. The shown arsenic
profile in Fig. 6.11 reveals that the critical junction depth of
27.5nm is not exceeded for the 65nm n-MOS transistor in this implantation
application. Finally, P. Kohli and R. Wise found that arsenic and boron
dopants show very little diffusion in the strained-Si/Si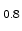 Ge
Ge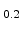 bilayer system by using a flash-assist RTA technique [26].
bilayer system by using a flash-assist RTA technique [26].
In optical transmission systems, an operation at 1.3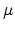 m and 1.55
m and 1.55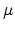 m
wavelengths is preferred due to the low attenuation in fiber-optic cables.
Germanium is an attractive candidate for high-speed photodetector applications
due to its high electron mobility and high optical absorption coefficient in
this wavelength range [133]. Recently, a bandwidth of 10GHz has been
demonstrated at a wavelength of 1.3
m
wavelengths is preferred due to the low attenuation in fiber-optic cables.
Germanium is an attractive candidate for high-speed photodetector applications
due to its high electron mobility and high optical absorption coefficient in
this wavelength range [133]. Recently, a bandwidth of 10GHz has been
demonstrated at a wavelength of 1.3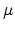 m for a PIN-photodiode, fabricated in
epitaxial Ge-on-Si technology [110]. The use of germanium is
advantageous over III-V compound materials in terms of lower fabrication
costs and feasible integration with silicon CMOS technology.
m for a PIN-photodiode, fabricated in
epitaxial Ge-on-Si technology [110]. The use of germanium is
advantageous over III-V compound materials in terms of lower fabrication
costs and feasible integration with silicon CMOS technology.
Figure 6.12:
Layout (left) and cross-section (right) of a high-speed
Ge-on-Si PIN photodetector with planar interdigitated p - and n
- and n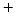 -fingers.
-fingers.
![\resizebox{1.0\linewidth}{!}{\rotatebox{0}{\includegraphics[clip]{figures/pin-layout}}}](img666.png)
|
Compositionally graded SiGe layers are deposited on the silicon wafer to achieve
a 1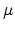 m thick germanium layer with a low defect density. In this doping
application, the interdigitated p
m thick germanium layer with a low defect density. In this doping
application, the interdigitated p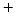 - and n
- and n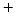 -finger regions of the photodetector
are formed by ion implantation. For this purpose, photoresist masks are used to
define the finger structure with a width of 1
-finger regions of the photodetector
are formed by ion implantation. For this purpose, photoresist masks are used to
define the finger structure with a width of 1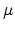 m and a spacing of 2
m and a spacing of 2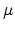 m.
Fig. 6.12 shows the schematic top and cross-sectional views of the
final PIN-photodetector. This large area photodetector consists of elementary
photodiodes which are connected in parallel. An elementary photodiode can be
defined as the three-dimensional region from the center of a p
m.
Fig. 6.12 shows the schematic top and cross-sectional views of the
final PIN-photodetector. This large area photodetector consists of elementary
photodiodes which are connected in parallel. An elementary photodiode can be
defined as the three-dimensional region from the center of a p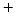 -finger to the
center of an n
-finger to the
center of an n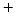 -finger.
-finger.
Figure 6.14:
Simulated 60keV arsenic implantation step for the
n -finger formation in germanium using a photoresist mask.
-finger formation in germanium using a photoresist mask.
|
Figure 6.13:
Simulated 15keV boron implantation step for the p -finger
formation in germanium using a photoresist mask. -finger
formation in germanium using a photoresist mask.
![\resizebox{1.0\linewidth}{!}{\rotatebox{0}{\includegraphics[clip]{figures/pin_B}}}](img667.png)
|
|
In the first process step the p -fingers are patterned and boron is implanted
with an energy of 15keV and a dose of
-fingers are patterned and boron is implanted
with an energy of 15keV and a dose of
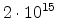 cm
cm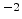 .
The three-dimensional boron distribution, as shown in Fig. 6.13, was obtained
by using a 5nm thick oxide scattering layer on top of germanium. In the second
process step the n
.
The three-dimensional boron distribution, as shown in Fig. 6.13, was obtained
by using a 5nm thick oxide scattering layer on top of germanium. In the second
process step the n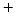 -fingers are formed by an implantation of arsenic with an
energy of 60keV and same dose. The shallow arsenic distribution in the simulated
device part is presented in Fig. 6.14. In spite of the lower implantation
energy, boron ions can penetrate much deeper into the germanium layer than arsenic
ions. Fig. 6.15 allows to compare the simulated boron and arsenic
profiles in the PIN-photodiode by using equal doping concentration isolines.
The reason for the large channeling tail of the boron profile lies mainly in
the small amount of produced point defects in germanium. The critical level of
point defects (Frenkel pairs) needed for amorphization of germanium is about
-fingers are formed by an implantation of arsenic with an
energy of 60keV and same dose. The shallow arsenic distribution in the simulated
device part is presented in Fig. 6.14. In spite of the lower implantation
energy, boron ions can penetrate much deeper into the germanium layer than arsenic
ions. Fig. 6.15 allows to compare the simulated boron and arsenic
profiles in the PIN-photodiode by using equal doping concentration isolines.
The reason for the large channeling tail of the boron profile lies mainly in
the small amount of produced point defects in germanium. The critical level of
point defects (Frenkel pairs) needed for amorphization of germanium is about
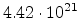 cm
cm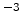 , one tenth of the germanium atomic
density [134]. Fig. 6.16 demonstrates that the arsenic
implantation has produced an amorphous zone, while the maximum defect concentration
of the boron implantation is significantly lower than the amorphization level.
The predicted damage results are consistent with experimental observations
obtained by processing a PIN-photodiode on a germanium substrate under similar
process conditions. In [135] it was found that the as-implanted resistance
of the boron implant was 201
, one tenth of the germanium atomic
density [134]. Fig. 6.16 demonstrates that the arsenic
implantation has produced an amorphous zone, while the maximum defect concentration
of the boron implantation is significantly lower than the amorphization level.
The predicted damage results are consistent with experimental observations
obtained by processing a PIN-photodiode on a germanium substrate under similar
process conditions. In [135] it was found that the as-implanted resistance
of the boron implant was 201
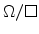 at a dose of
at a dose of
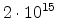 cm
cm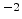 ,
while that for the arsenic implant was not measurable. This fact strongly
indicates that boron-implanted germanium remains crystalline at least up to
the used dose, while arsenic-implanted germanium becomes amorphous.
,
while that for the arsenic implant was not measurable. This fact strongly
indicates that boron-implanted germanium remains crystalline at least up to
the used dose, while arsenic-implanted germanium becomes amorphous.
6.4 NBTI Lifetime Analysis of a CMOS SRAM Cell
Conventional six-transistor CMOS SRAM cell structures are dominantly employed in
today's cache memory blocks for advanced microprocessors. The long-term stability
of such a CMOS memory cell is strongly affected by NBTI induced degradation of
MOSFET parameters (e.g. threshold voltage) which leads to a reduction in the
static noise margin (SNM) of the cell [136]. As explained in Section 5,
negative bias temperature instability (NBTI) in p-MOSFETs with nitrided gate
oxides has emerged as the dominant degradation mechanism for newer CMOS
technologies. The AC degradation is significantly lower than the DC degradation
for any given stress time, since the interface traps generated during the
on-state of the MOSFET are partially annealed in the off-state (dynamic NBTI effect).
While transistor degradation in CMOS-based NAND circuits depends on the AC
operating conditions (e.g. clock frequency), in SRAM cells it is possible that
a stored bit value does not change for a long time. On the other hand, it would
be to strict to equate the lifetime of an SRAM transistor with its DC lifetime.
The two p-MOSFETs employed in a 6T-SRAM cell are unsymmetrically NBT stressed
by the stored bit values. The split of on-state times between the two devices
(only either of them is ``on'') lies well within the boundaries of pure DC
stress (100/0 stress-split) and symmetric AC stress (50/50 stress-split).
Only a periodically flipping of the bit with comparable on-times would lead
to equal parameter degradation of both devices and hence to the longest lifetime
of the SRAM cell. The worst-case lifetime of an SRAM cell can be determined
by storing a random bit sequence where the probability is, for instance, 90%
for storing a ``one'' (or 90% for storing a ``zero'') which corresponds to
a 90/10 NBT stress-split. In this simulation study, NBTI responses to random
bit sequences are studied by using a calibrated reaction-diffusion
model [137].
The investigated SRAM cell, shown in Fig. 6.17, was fabricated in a 90nm
process technology. The cell consists of two cross-coupled CMOS inverters (T1,
T2 and T3, T4) and the access transistors T5 and T6. While the p-MOSFETs T2
and T4 are affected by NBTI as long as the power is supplied to the cell (at
least either of them), the parameter degradation of the comprised n-MOSFETs
is neglected in this study. In the high state of the flip-flop (node BIT is
high), T2 is under NBT stress, and in the other state (BIT low), T4 is stressed.
The performed NBTI measurements for the 90nm p-MOSFET device are described
in Section 5.
Figure 6.17:
Schematic (left) and layout (right) of the investigated
6T-SRAM cell.
|
|
Fig. 6.18 shows the NBTI induced 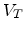 parameter degradation of the
MOSFET T2 for storing a bit value every second in the memory cell, whereby the
probability is 90% for storing a ``one''. The worst-case parameter degradation
of T2/T4 lies always in the range between the envelope degradation curves under
DC and under symmetric AC stress. Due to the high unsymmetry between the turn on
and off times at a ratio of 90/10 for T2, the
parameter degradation of the
MOSFET T2 for storing a bit value every second in the memory cell, whereby the
probability is 90% for storing a ``one''. The worst-case parameter degradation
of T2/T4 lies always in the range between the envelope degradation curves under
DC and under symmetric AC stress. Due to the high unsymmetry between the turn on
and off times at a ratio of 90/10 for T2, the 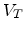 degradation lies closer to
the DC boundary than to the symmetric AC boundary. Fig. 6.19 shows the
zoomed-in time diagram of the beginning phase from Fig. 6.18 (first 150
seconds), where the progression of the NBTI response of T2 and the corresponding
random gate drive signal can be seen more clearly. The rectangular gate signal
of the simulation was derived from a random-number generator which produces
uniformly distributed random variates in the interval
degradation lies closer to
the DC boundary than to the symmetric AC boundary. Fig. 6.19 shows the
zoomed-in time diagram of the beginning phase from Fig. 6.18 (first 150
seconds), where the progression of the NBTI response of T2 and the corresponding
random gate drive signal can be seen more clearly. The rectangular gate signal
of the simulation was derived from a random-number generator which produces
uniformly distributed random variates in the interval ![$ [0, 1]$](img289.png) .
In the simulation presented in Fig. 6.20, the overall stress time of
T2 is further increased by storing a random bit sequence with a probability of
95% for a one. It can be observed that the NBTI response curve converges to
the DC degradation envelope since the annealing of interface traps during the
unfrequent ``high'' states of the gate signal is not sufficient to reduce the
parameter degradation significantly from the degradation under DC stress.
A data flipping technique for SRAM arrays is proposed in [136] to solve
the problem of highly unsymmetrical NBTI induced degradation of p-MOSFET devices
in SRAM cells. The periodic flipping of the contents of all SRAM cells, e.g.
every 10
.
In the simulation presented in Fig. 6.20, the overall stress time of
T2 is further increased by storing a random bit sequence with a probability of
95% for a one. It can be observed that the NBTI response curve converges to
the DC degradation envelope since the annealing of interface traps during the
unfrequent ``high'' states of the gate signal is not sufficient to reduce the
parameter degradation significantly from the degradation under DC stress.
A data flipping technique for SRAM arrays is proposed in [136] to solve
the problem of highly unsymmetrical NBTI induced degradation of p-MOSFET devices
in SRAM cells. The periodic flipping of the contents of all SRAM cells, e.g.
every 10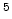 seconds, can be performed either by software or hardware.
seconds, can be performed either by software or hardware.
Long-time simulations were performed at a supply voltage of 1.5V under DC and
under symmetric AC stress with a 10Hz rectangular gate signal to determine the
boundaries for the SRAM lifetime. Fig. 6.21 shows the lifetime extension of the
cell due to the dynamic NBTI effect. The lifetime was defined here as a 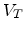 shift of 40mV for the p-MOSFETs. The AC lifetime for a symmetric gate signal
operation at 10Hz would be 1.7 times longer than the DC lifetime of the cell.
The SRAM lifetime for storing a random bit sequence with a probability of
90% for storing a one bit (or 90% for a zero bit) is 1.14 times longer than
the DC lifetime.
shift of 40mV for the p-MOSFETs. The AC lifetime for a symmetric gate signal
operation at 10Hz would be 1.7 times longer than the DC lifetime of the cell.
The SRAM lifetime for storing a random bit sequence with a probability of
90% for storing a one bit (or 90% for a zero bit) is 1.14 times longer than
the DC lifetime.
Figure 6.18:
Comparison of storing random bit values every
second in the cell with 90% probability for a one to DC and AC degradation of
transistor T2.
![\resizebox{1.0\linewidth}{!}{\rotatebox{0}{\includegraphics[clip]{figures/rand90demo}}}](img675.png)
|
Figure 6.19:
Comparison of storing random bit values every
second with 90% probability for a one to DC and AC degradation of
T2 for early stress times.
![\resizebox{1.0\linewidth}{!}{\rotatebox{0}{\includegraphics[clip]{figures/rand90zoom}}}](img676.png)
|
Figure 6.20:
Comparison of random bit sequences with 95%
probability for one to DC and AC degradation of T2.
![\resizebox{1.0\linewidth}{!}{\rotatebox{0}{\includegraphics[clip]{figures/rand95demo}}}](img677.png)
|
Figure 6.21:
Simulated lifetime extension of the SRAM cell related to
the DC lifetime of the cell for different on-time probabilities of T2.
![\resizebox{1.0\linewidth}{!}{\rotatebox{0}{\includegraphics[clip]{figures/lt}}}](img678.png)
|



Next: 7. Summary and Conclusion
Up: Dissertation Robert Wittmann
Previous: 5. NBTI Reliability Analysis
R. Wittmann: Miniaturization Problems in CMOS Technology: Investigation of Doping Profiles and Reliability
![\resizebox{1.1\linewidth}{!}{\rotatebox{0}{\includegraphics[clip]{figures/struct_as-comb}}}](img643.png)
![\resizebox{1.05\linewidth}{!}{\rotatebox{0}{\includegraphics[clip]{figures/shallow_as}}}](img644.png)
![\resizebox{1.0\linewidth}{!}{\rotatebox{0}{\includegraphics[clip]{figures/As_LAT-1D}}}](img645.png)
![]() , and a tilt of 30
, and a tilt of 30![]() . The Monte Carlo
simulation was carried out with four million particles for each implantation
step. The simulation domain and the external implantation window were both
expanded by about 50nm perpendicular to the front, back, left, and right
boundaries of the input geometry to avoid any boundary influence for the
dopant distribution at the surface of the device structure.
. The Monte Carlo
simulation was carried out with four million particles for each implantation
step. The simulation domain and the external implantation window were both
expanded by about 50nm perpendicular to the front, back, left, and right
boundaries of the input geometry to avoid any boundary influence for the
dopant distribution at the surface of the device structure.
![\resizebox{1.089\linewidth}{!}{\rotatebox{0}{\includegraphics[clip]{figures/quadimpl_b}}}](img655.png)
![]() /Si layer structure
were simulated with
/Si layer structure
were simulated with
![]() ion trajectories by using the same
implantation conditions as for the three-dimensional test structure.
Fig. 6.6 demonstrates that all four boron implantations yield the
same doping profile since the used ion beam directions are
crystallographically identical.
ion trajectories by using the same
implantation conditions as for the three-dimensional test structure.
Fig. 6.6 demonstrates that all four boron implantations yield the
same doping profile since the used ion beam directions are
crystallographically identical.
![\resizebox{1.0\linewidth}{!}{\rotatebox{0}{\includegraphics[clip]{figures/As_SSi_diss}}}](img662.png)
![]() .
Fig. 6.8 shows the arsenic distribution in the device structure
without sidewall spacer after smoothing of the Monte Carlo result and
translating it to the destination mesh. For the ion implantation simulation
of the source/drain extensions, the nitride spacer segment is cut off from
the meshed transistor structure. Fig. 6.9 shows the meshed
structure required to simulate the second implantation step in the two-step
sequence. While no additional segments can be added to a final meshed device
structure, any non-required segment of the structure can be removed.
.
Fig. 6.8 shows the arsenic distribution in the device structure
without sidewall spacer after smoothing of the Monte Carlo result and
translating it to the destination mesh. For the ion implantation simulation
of the source/drain extensions, the nitride spacer segment is cut off from
the meshed transistor structure. Fig. 6.9 shows the meshed
structure required to simulate the second implantation step in the two-step
sequence. While no additional segments can be added to a final meshed device
structure, any non-required segment of the structure can be removed.
![]() .
Fig. 6.10 shows the simulated cross-section along the channel of the
strained n-MOSFET after performing the source/drain implants. In this
application the Monte Carlo simulation was carried out with
.
Fig. 6.10 shows the simulated cross-section along the channel of the
strained n-MOSFET after performing the source/drain implants. In this
application the Monte Carlo simulation was carried out with
![]() ion trajectories per implantation step to achieve a
low statistical fluctuation of the predicted doping profiles.
ion trajectories per implantation step to achieve a
low statistical fluctuation of the predicted doping profiles.
![]() Ge
Ge![]() bilayer system by using a flash-assist RTA technique [26].
bilayer system by using a flash-assist RTA technique [26].
![\resizebox{1.0\linewidth}{!}{\rotatebox{0}{\includegraphics[clip]{figures/pin-layout}}}](img666.png)
![]() m thick germanium layer with a low defect density. In this doping
application, the interdigitated p
m thick germanium layer with a low defect density. In this doping
application, the interdigitated p![]() - and n
- and n![]() -finger regions of the photodetector
are formed by ion implantation. For this purpose, photoresist masks are used to
define the finger structure with a width of 1
-finger regions of the photodetector
are formed by ion implantation. For this purpose, photoresist masks are used to
define the finger structure with a width of 1![]() m and a spacing of 2
m and a spacing of 2![]() m.
Fig. 6.12 shows the schematic top and cross-sectional views of the
final PIN-photodetector. This large area photodetector consists of elementary
photodiodes which are connected in parallel. An elementary photodiode can be
defined as the three-dimensional region from the center of a p
m.
Fig. 6.12 shows the schematic top and cross-sectional views of the
final PIN-photodetector. This large area photodetector consists of elementary
photodiodes which are connected in parallel. An elementary photodiode can be
defined as the three-dimensional region from the center of a p![]() -finger to the
center of an n
-finger to the
center of an n![]() -finger.
-finger.
![]() parameter degradation of the
MOSFET T2 for storing a bit value every second in the memory cell, whereby the
probability is 90% for storing a ``one''. The worst-case parameter degradation
of T2/T4 lies always in the range between the envelope degradation curves under
DC and under symmetric AC stress. Due to the high unsymmetry between the turn on
and off times at a ratio of 90/10 for T2, the
parameter degradation of the
MOSFET T2 for storing a bit value every second in the memory cell, whereby the
probability is 90% for storing a ``one''. The worst-case parameter degradation
of T2/T4 lies always in the range between the envelope degradation curves under
DC and under symmetric AC stress. Due to the high unsymmetry between the turn on
and off times at a ratio of 90/10 for T2, the ![]() degradation lies closer to
the DC boundary than to the symmetric AC boundary. Fig. 6.19 shows the
zoomed-in time diagram of the beginning phase from Fig. 6.18 (first 150
seconds), where the progression of the NBTI response of T2 and the corresponding
random gate drive signal can be seen more clearly. The rectangular gate signal
of the simulation was derived from a random-number generator which produces
uniformly distributed random variates in the interval
degradation lies closer to
the DC boundary than to the symmetric AC boundary. Fig. 6.19 shows the
zoomed-in time diagram of the beginning phase from Fig. 6.18 (first 150
seconds), where the progression of the NBTI response of T2 and the corresponding
random gate drive signal can be seen more clearly. The rectangular gate signal
of the simulation was derived from a random-number generator which produces
uniformly distributed random variates in the interval ![]() .
In the simulation presented in Fig. 6.20, the overall stress time of
T2 is further increased by storing a random bit sequence with a probability of
95% for a one. It can be observed that the NBTI response curve converges to
the DC degradation envelope since the annealing of interface traps during the
unfrequent ``high'' states of the gate signal is not sufficient to reduce the
parameter degradation significantly from the degradation under DC stress.
A data flipping technique for SRAM arrays is proposed in [136] to solve
the problem of highly unsymmetrical NBTI induced degradation of p-MOSFET devices
in SRAM cells. The periodic flipping of the contents of all SRAM cells, e.g.
every 10
.
In the simulation presented in Fig. 6.20, the overall stress time of
T2 is further increased by storing a random bit sequence with a probability of
95% for a one. It can be observed that the NBTI response curve converges to
the DC degradation envelope since the annealing of interface traps during the
unfrequent ``high'' states of the gate signal is not sufficient to reduce the
parameter degradation significantly from the degradation under DC stress.
A data flipping technique for SRAM arrays is proposed in [136] to solve
the problem of highly unsymmetrical NBTI induced degradation of p-MOSFET devices
in SRAM cells. The periodic flipping of the contents of all SRAM cells, e.g.
every 10![]() seconds, can be performed either by software or hardware.
seconds, can be performed either by software or hardware.
![]() shift of 40mV for the p-MOSFETs. The AC lifetime for a symmetric gate signal
operation at 10Hz would be 1.7 times longer than the DC lifetime of the cell.
The SRAM lifetime for storing a random bit sequence with a probability of
90% for storing a one bit (or 90% for a zero bit) is 1.14 times longer than
the DC lifetime.
shift of 40mV for the p-MOSFETs. The AC lifetime for a symmetric gate signal
operation at 10Hz would be 1.7 times longer than the DC lifetime of the cell.
The SRAM lifetime for storing a random bit sequence with a probability of
90% for storing a one bit (or 90% for a zero bit) is 1.14 times longer than
the DC lifetime.
![\resizebox{1.0\linewidth}{!}{\rotatebox{0}{\includegraphics[clip]{figures/rand90demo}}}](img675.png)
![\resizebox{1.0\linewidth}{!}{\rotatebox{0}{\includegraphics[clip]{figures/rand90zoom}}}](img676.png)
![\resizebox{1.0\linewidth}{!}{\rotatebox{0}{\includegraphics[clip]{figures/rand95demo}}}](img677.png)
![\resizebox{1.0\linewidth}{!}{\rotatebox{0}{\includegraphics[clip]{figures/lt}}}](img678.png)