Next: 4.2 Ordnungsreduktionverfahren Up: 4. Simulation von Verbindungsleitungen Previous: 4. Simulation von Verbindungsleitungen
Analytische Berechnung der Kapazitäten wird kaum angewandt, weil selbst für
einfache Geometrien ein großer Aufwand nötig ist, um die Gleichungen zu
erhalten. Manchmal wird zur Kalibrierung mit Teststrukturen, die mit
Näherungsformeln berechnet werden, auf die analytische Berechnung
zurückgegriffen.
Geometrische Modelle approximieren die Werte der Kapazitäten auf Basis von
Näherungsformeln an. Dabei wird z.B. bei benachbarten Leitungen die
Kapazität bestimmt aufgrund eines Anteils der überlappenden Fläche und eines
Anteils verursacht durch das Streufeld.
Diese Modelle sind kalibriert für eine spezifische Technologie, die
bei Änderungen von wesentlichen Parametern in einem langwierigen
Procedere wieder angepaßt werden müssen. Sie werden häufig zur
Parameterextraktion der gesamten Verdrahtungsstruktur von integrierten
Schaltungen verwendet.
Dreidimensionale Feldgleichungslöser sind die allgemeinste Form zur
elektromagnetischen Analyse, weil sie direkt die
partiellen Differentialgleichungen lösen. Zwei populäre numerische
Methoden sind die Boundary Element Methode (BEM) und die Finite Elemente
Methode (FEM).
Die BEM [85,86,87] nutzt eine Integralformulierung basierend auf dem Green-Theorem
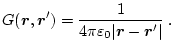 |
(4.2) |
Falls das Simulationsgebiet aus mehreren Materialien mit unterschiedlichen
Permittivitäten besteht, müssen auch die Grenzschichten zwischen diesen
Materialien mit den Randelementen diskretisiert werden, um die
Polarisationsladung zu berücksichtigen. Um die daraus resultierende Vergrößerung der Systemmatrix zu vermeiden,
können geeignete Green-Funktionen benutzt werden, die die verschiedenen
Dielektrika mitsamt den Polarisationsladungen an den Grenzflächen
repräsentieren [90].
Die passende Green-Funktion für mehrere Materialien mit unterschiedlichen
Dielektrizitätszahlen ist meist schwierig zu finden [91].
Die Finite Elemente Methode sucht in jedem Element nach einer
Näherungslösung, die durch geeignete Wahl der Ansatzfunktionen mit hoher
Genauigkeit erreicht werden kann. Diese
Ansatzfunktionen sind den Gitterpunkten zugeordnet und entweder an die
erwartete Lösung oder an die Eigenfunktionen des Differentialoperators
angepaßt. Eine gute Näherung erhält man, indem gefordert wird, dass das mit
den Gewichtsfunktionen multiplizierte Residuum (Differenz zwischen exakter
Lösung und Näherungslösung) im Mittel verschwindet. Eine gebräuchliche
Methode ist die Gewichtsfunktionen den Ansatzfunktionen gleichzusetzen
(Galerkin-Ansatz).
Finite Elemente [92] Diskretisierung führt auf eine spärlich
besetzte Matrix, die um etliches größer ist als jene der BEM, weil das
ganze Simulationsgebiet mit Volumselementen diskretisiert ist. Die FEM ist überaus flexibel und gestattet inhomogene, anisotrope, oder
nichtlineare Dielektrika. Hohe Genauigkeit wird erzielt durch Anwendung von
Gitterverfeinerung bzw. höhere Ordnung der Ansatzfunktionen.
Im Gegensatz zur BEM, wo die Greenschen Funktionen das elektrische Feld bis
Unendlich repräsentieren, ist der Simulationsbereich bei der FEM begrenzt,
üblicherweise durch homogene Neumann-Randbedingungen. Verglichen mit der
BEM, ist die FEM nicht auf homogene, geschichtete Dielektrika begrenzt;
allerdings ist der Berechnungsaufwand größer als für die beschleunigte BEM.
Abbildung 4.1 zeigt ein Beispiel, für das die FEM genutzt wurde, um die
Kapazität zweier Leiter über Erde zu ermitteln.
Für die partiellen Kapazitäten eines ![]() -Leiterproblems sind
-Leiterproblems sind ![]() Simulationen mit verschiedenen Feldkonfigurationen der Leiter durchzuführen.
Die Abbildung zeigt zwei Konfigurationen, die mit Äquipotentialflächen
(rot
Simulationen mit verschiedenen Feldkonfigurationen der Leiter durchzuführen.
Die Abbildung zeigt zwei Konfigurationen, die mit Äquipotentialflächen
(rot ![]() V, blau
V, blau ![]() V) im Dielektrikum dargestellt sind.
V) im Dielektrikum dargestellt sind.
![\includegraphics[width=0.49\textwidth]{pl1}\hfil%
\includegraphics[width=0.49\textwidth]{pl2}](img250.png) |
Kombinationen von BEM und FEM, sogenannte Hybridelementmethoden,
versuchen die Vorteile von beiden zu vereinen [93].
Spezielle Modelle an den Grenzschichten sind erforderlich. Ein Nachteil der Hybridelementmethode ist die Notwendigkeit einer
geometrischen Selektion, um die Simulationsbereiche der BEM und FEM
festzulegen. Der Gittergenerator muss sowohl Randelemente, als auch
Volumselemente unterstützen. In der Praxis werden Hybridelementmethoden
allerdings kaum eingesetzt.
Eine andere Methode zur Berechnung der Kapazitäten ist die Anwendung
Finiter Differenzen um die Ableitungen der Differentialoperatoren durch
Differenzquotienten zu ersetzen [94]. Dabei erhält man auf dem
typisch verwendeten strukturierten Gitter für jeden Knoten eine Gleichung in
den unbekannten Funktionswerten des Gitterpunktes und seiner Nachbarn. Daraus
resultiert eine spärlich besetzte Systemmatrix, die mit iterativen Verfahren
effizient gelöst werden kann. In [95,96,97,98] wird mittels ![]() Finiter Differenzen'' eine
Diskretisierung der kompletten Maxwell-Gleichungen und eine Lösung im
Zeitbereich erreicht.
Finiter Differenzen'' eine
Diskretisierung der kompletten Maxwell-Gleichungen und eine Lösung im
Zeitbereich erreicht.
Ein bekanntes stochastisches Verfahren ist die ``Random Walk
Methode'' (RWM) [99]. Besonders attraktiv ist dieses
Verfahren, weil kein Gitter benötigt wird, und aufgrund des geringen
Rechenaufwands sehr große Simulationsgebiete mit geringem Speicherbedarf
analysiert werden können. Grobe Abschätzungen der berechneten Kapazitäten sind
bereits nach wenigen Iterationen verfügbar, der Fehler sinkt reziprok mit der
Wurzel der Auswertungen.
Diese Methode basiert auf der Lösung der Laplace-Gleichung in einem skalierbaren Würfel mit verschiedenen Dirichlet-Bedingungen. Mithilfe eines Randintegrals werden das Potenzial und das elektrische Feld im Zentrum des Würfels berechnet. Die Kapazität zwischen zwei beliebigen Elektroden kann nun als unendliche Reihe verschachtelter Randintegrale ausgedrückt werden. Aus dieser Reihe lassen sich Wahrscheinlichkeitsregeln für sogenannte ``Random Walks`` herleiten. Man geht dabei schrittweise von einer Elektrode aus und findet einen maximal großen um den Startpunkt zentrierten Würfel, dessen Innenraum keine Elektrode enthält. Der Startpunkt für den nächsten Schritt liegt immer auf der Oberfläche des vorigen Würfels. Beendet wird der Random Walk wenn eine andere Elektrode erreicht wird (Abb. 4.2). Durch gewichtete Summierung kann man die Kapazitäten zwischen Startelektrode und allen anderen Leitern ermitteln.
![\begin{figure}{\resizebox{0.52\textwidth}{!}{\includegraphics[{}]{random}}}\end{figure}](img255.png) |
Die BEM ist sehr effizient für genaue Kapazitätsberechnung, für die Extraktion der Kapazitäten eines Chips ist sie aber ebensowenig geeignet wie die FEM, hauptsächlich weil der Bedarf an Speicherressourcen gravierend ist. Eine Möglichkeit ist deshalb den Entwurf in kleinere Bereiche aufzuteilen, und separat zu behandeln. Ein weiteres Beispiel für die Aufteilung des Entwurfs ist die Einführung eines Tunnels, in dem kritische Netze und alle Nachbarleitungen berücksichtigt werden. Da die Größe des Tunnels Auswirkung auf die erzielbare Genauigkeit hat, darf er nicht zu klein gewählt werden. Dieses Verfahren muss für alle Netze wiederholt werden um die Kapazitäten des ganzen Chips zu erhalten [100]. Inhomogene und nichtlineare Materialien können mit der BEM oder der ``Random Walk Methode'' nicht berechnet werden.
Zur Berechnung von induktiven Effekten wird die Methode der partiellen
Induktivitäten benötigt, die bereits in Abschnitt 1.6
vorgestellt wurde. Nachdem langwierige analytische Formulierungen, wie z.B.
in [41] für rechteckige Leiter angegeben, sich nicht besonders
für eine rechnerunterstützte Auswertung eignen, gibt es in [102]
verbesserte computergerechtere Formeln für lange, dünne Leiter. Eine
geschlossene Lösung mit 16 Auswertungen einer Funktion für Rechteckleiter
bietet [103] an. Durch Segmentierung der Leiter wird eine Modellierung
des Skineffektes möglich. Die Netzwerktheorie nützend, wird nicht explizit
die Stromdichte ausgerechnet, sondern die Stromdichteverteilung angenähert
durch kleine Zellen, die konstante Stromdichten aufweisen. Von Zelle zu Zelle kann
die Stromdichte variieren, sodass man eine Treppenfunktion-Näherung der
aktuellen Stromdichte erhält.
Exemplarisch
wird auf ein Simulationsprogramm eingegangen, das auf Näherungsformeln,
allerdings von [40] zurückgreift. Der Ansatz dieses Programms geht
auf [104,105] zurück. Weiters wird in diesem Abschnitt
über andere Simulatoren berichtet, die entweder die Neumann-Formel numerisch
auswerten, oder einen Ansatz mit dem Vektorpotenzial verfolgen.
FastHenry [106] basiert auf einer Integralformulierung einer quasistatischen Lösung der Maxwell-Gleichungen.
Dazu wird das elektrische Feld
![]() entsprechend (3.9) aus dem Skalarpotenzial
entsprechend (3.9) aus dem Skalarpotenzial ![]() und dem
Vektorpotenzial
und dem
Vektorpotenzial
![]() angesetzt, und für harmonische Größen im
eingeschwungenen Zustand erhält man
angesetzt, und für harmonische Größen im
eingeschwungenen Zustand erhält man
| (4.3) |
Mit Verwendung der Coulomb-Eichung kann für das Skalarpotenzial und das Vektorpotenzial, gegeben durch (3.19), folgende Integralgleichung formuliert werden:
Durch gleichzeitiges Lösen von (4.4) mit der Sicherstellung der Quellenfreiheit
des Leiterstroms (3.34) erhält man Stromdichten und das elektrische
Skalarpotenzial der Leiter. Die Quellenfreiheit der Stromdichte wird durch
Lösen der Kirchhoffschen Spannungsregel erfüllt.
Die Integralgleichung wird gelöst durch Diskretisierung der Geometrie in dreidimensionale Zellen entsprechend Abb. 4.3. Dabei wird jeder Leiter aus geraden Teilstücken zusammengesetzt. Der Strom innerhalb jeder Zelle wird als konstant angenommen, wodurch die unbekannte Stromdichteverteilung geschrieben werden kann als
Dann wird (4.4) in Matrixschreibweise
Die Induktivitäten ergeben sich dann aus der komplexen Impedanzmatrix, die
den Zusammenhang zwischen der angelegten Spannung ![]() und dem
Leiterstrom
und dem
Leiterstrom ![]() für das jeweilige Leitersystem
herstellt. Diese Induktivitätsextraktion vernachlässigt den Einfluss von
Kapazitäten auf den Stromfluß, was zu Ungenauigkeiten führen kann, weil der
Rückstrompfad stark durch parasitäre Kapazitäten beeinflußt
wird [107].
für das jeweilige Leitersystem
herstellt. Diese Induktivitätsextraktion vernachlässigt den Einfluss von
Kapazitäten auf den Stromfluß, was zu Ungenauigkeiten führen kann, weil der
Rückstrompfad stark durch parasitäre Kapazitäten beeinflußt
wird [107].
Ähnliche Integralformulierungen sind veröffentlicht worden, auch
Retardierungseffekte werden darin berücksichtigt. Dies ist dann äquivalent zur
Wellenlösung der Maxwell-Gleichungen [108,109,110,111].
Andere Simulatoren wie z.B. [112] greifen ebenfalls wie FastHenry auf
Näherungsformeln von Grover [40] oder andere Ausdrücke für
partielle Induktivitäten von einfachen Geometrien zurück. Dieser Simulator
benützt ebenfalls die Einschränkung bezüglich der Geometrie (auf
Rechteckleiter und z.B. ebene, geschichte Dielektrika) und durch Ausnützung
von Symmetrien gelingt eine Ableitung von Green-Funktionen, die eine zusätzliche Extraktion von C ermöglicht.
Ebenfalls, wie in dieser Arbeit wird in [113] die Monte Carlo Methode
benutzt, um aus der Neumann-Formel partielle Induktivitäten zu berechnen.
Dort wird ein klassischer Ansatz für die Implementierung der Monte Carlo
Methode verfolgt, und Varianzreduktionsschemata auf Geometrien mit strukturiertem Gitter durchgeführt.
In [114] wird für ein einfaches Beispiel eine quasistatische
Näherung gezeigt, wie eine aufgrund des Skineffekts zeitabhängige
Induktivitätsmatrix ermittelt
werden kann, indem nach der Berechnung von
![]() und
und
![]() , diese
beiden Größen durch eine Darstellung von Basisfunktionen entsprechend der
Separation von Zeit- und Raum-Variablen ersetzt werden. Dabei wird an der
Formulierung von Bíró [115] festgehalten, die die Eindeutigkeit des
Vektorpotenzials sicherstellt. Die Finite Elemente Simulation basiert auf
klassischen Knotenelementen. In diesem Ansatz werden folgende Gleichungen
, diese
beiden Größen durch eine Darstellung von Basisfunktionen entsprechend der
Separation von Zeit- und Raum-Variablen ersetzt werden. Dabei wird an der
Formulierung von Bíró [115] festgehalten, die die Eindeutigkeit des
Vektorpotenzials sicherstellt. Die Finite Elemente Simulation basiert auf
klassischen Knotenelementen. In diesem Ansatz werden folgende Gleichungen
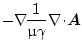 auf der linken Seite
in (4.10) und der Anwendung der Randbedingungen nach Bíró
(s. auch Abschnitt 7.1) gewährleistet.
auf der linken Seite
in (4.10) und der Anwendung der Randbedingungen nach Bíró
(s. auch Abschnitt 7.1) gewährleistet.
Für die Berechnung der Maxwell-Gleichungen wird häufig die Finite
Differenzen Methode benutzt. Dabei werden die Feldgrößen allerdings direkt
-- ohne Verwendung von Skalar- und Vektorpotenzial -- berechnet, als
Beispiel sei [116] angeführt. Dies wird
meistens auf strukturiertem Gitter durchgeführt. Ebenfalls beliebige
quaderförmige Strukturen werden in [117] behandelt. In der dort
verwendeten Formulierung der elektromagnetische Analyse wird auf das
magnetische Vektorpotenzial und das elektrische Skalarpotenzial
zurückgegriffen. Zur numerischen Stabilität der Implementierung werden die
Potenziale über die Konstante4.2 ![]() mit einem Eichungsfeld
mit einem Eichungsfeld ![]() verknüpft [118],
sodass für den stationären Fall folgende Gleichungen gelöst werden:
verknüpft [118],
sodass für den stationären Fall folgende Gleichungen gelöst werden:
Obengenannte Methoden sind durchwegs für bescheiden große
Simulationsgebiete geeignet. Entsprechend dem Ansatz sind große Unterschiede
bezüglich Rechenzeit und Speicher zu erwarten.
Auffällig ist, dass fast ausschließlich Geometrien behandelt werden, die sich durch quaderförmige Gitterelemente
darstellen lassen. Daher sind diese Ansätze praktisch nicht geeignet zur Berücksichtigung des Herstellungsprozesses auf
die Geometrie.
Zur Berechnung von partiellen Selbst- und Gegeninduktivitäten eines ganzen
Chips werden Formeln aus [40,120] verwendet.
Die resultierende Matrix ![]() der partiellen Induktivitäten besitzt eine
unhandliche Größe und Dichte, sodass sie direkt nicht brauchbar ist für
Analysezwecke eines ganzen Chips. Weiters ist sie vollbesetzt, symmetrisch und
nicht diagonal dominant. Eine gewöhnliche Behandlung der Matrix wäre alle
Kopplungen von weit entfernten Leitern zu ignorieren. Dies führt allerdings
zu instabilen Stromkreismodellen mit negativen Eigenwerten der Matrix,
während die ganze partielle Induktivitätenmatrix
der partiellen Induktivitäten besitzt eine
unhandliche Größe und Dichte, sodass sie direkt nicht brauchbar ist für
Analysezwecke eines ganzen Chips. Weiters ist sie vollbesetzt, symmetrisch und
nicht diagonal dominant. Eine gewöhnliche Behandlung der Matrix wäre alle
Kopplungen von weit entfernten Leitern zu ignorieren. Dies führt allerdings
zu instabilen Stromkreismodellen mit negativen Eigenwerten der Matrix,
während die ganze partielle Induktivitätenmatrix ![]() immer positiv definit
ist. Eine theoretische Analyse, welche weit entfernten Leiter noch
berücksichtigt werden müssen, ist schwierig durchzuführen; eine empirische
Studie zeigt, dass beinahe alle berücksichtigt werden müssen, um
positive Eigenwerte zu erhalten. [121] zeigt eine Methode auf, die
eine symmetrische, stabile, spärlich besetzte Matrix erzeugt.
Dazu wird eine künstliche Stromverteilung für jedes Teilstück der Schleife
auf einer Äquipotentialoberfläche angelegt, die außerhalb dieser
Oberfläche das Vektorpotenzial der Originalverteilung ideal kompensiert.
Die Kopplungen zu weit entfernten Teilstücken werden Null und
stellen die Stabilität der Matrix sicher. Innerhalb dieser Oberfläche
wird das Vektorpotenzial um einen konstanten Wert verschoben. Diese Änderung
betrifft nur die partiellen Induktivitäten. Die Schleifeninduktivitäten
bleiben erhalten, wenn jedes Teilstück (der gesamten Schleife) eine
Oberfläche besitzt, die groß genug ist, um alle anderen Teilstücke der
Schleife zu umfassen.
immer positiv definit
ist. Eine theoretische Analyse, welche weit entfernten Leiter noch
berücksichtigt werden müssen, ist schwierig durchzuführen; eine empirische
Studie zeigt, dass beinahe alle berücksichtigt werden müssen, um
positive Eigenwerte zu erhalten. [121] zeigt eine Methode auf, die
eine symmetrische, stabile, spärlich besetzte Matrix erzeugt.
Dazu wird eine künstliche Stromverteilung für jedes Teilstück der Schleife
auf einer Äquipotentialoberfläche angelegt, die außerhalb dieser
Oberfläche das Vektorpotenzial der Originalverteilung ideal kompensiert.
Die Kopplungen zu weit entfernten Teilstücken werden Null und
stellen die Stabilität der Matrix sicher. Innerhalb dieser Oberfläche
wird das Vektorpotenzial um einen konstanten Wert verschoben. Diese Änderung
betrifft nur die partiellen Induktivitäten. Die Schleifeninduktivitäten
bleiben erhalten, wenn jedes Teilstück (der gesamten Schleife) eine
Oberfläche besitzt, die groß genug ist, um alle anderen Teilstücke der
Schleife zu umfassen.
Zur Induktivitätsextraktion des ganzen Chips schlägt [122] vor,
Formeln oder Bibliotheken anzuwenden, die auf der inversen partiellen
Induktivitätsmatrix beruht. Diese Matrix ![]() hat ähnliche Eigenschaften
wie die Kapazitätsmatrix
hat ähnliche Eigenschaften
wie die Kapazitätsmatrix ![]() , wenngleich festgestellt werden muss, dass
diese keine Kapazitätsmatrix ist. Wichtigster Vorteil der Matrix
, wenngleich festgestellt werden muss, dass
diese keine Kapazitätsmatrix ist. Wichtigster Vorteil der Matrix ![]() ist
der lokale Charakter, nur eine kleine Anzahl von Nachbarn muss berücksichtigt
werden. Die spärlich besetzte Matrix, die weit entfernte Leiter ignoriert,
ist immer positiv definit.
Der Beweis dafür ist in [123] ausgeführt: Ausgehend vom Beweis des
lokalen Charakters der Matrix (
ist
der lokale Charakter, nur eine kleine Anzahl von Nachbarn muss berücksichtigt
werden. Die spärlich besetzte Matrix, die weit entfernte Leiter ignoriert,
ist immer positiv definit.
Der Beweis dafür ist in [123] ausgeführt: Ausgehend vom Beweis des
lokalen Charakters der Matrix (
![]() ) wird
anhand der Definition der Schleifeninduktivität (3.45) gezeigt,
dass [K] eine strikt diagonaldominante Matrix ist für deren Elemente
) wird
anhand der Definition der Schleifeninduktivität (3.45) gezeigt,
dass [K] eine strikt diagonaldominante Matrix ist für deren Elemente