7.1 Der Einzeltransistor




Next: 7.2 DMOS-Schaltungen
Up: 7 Ergebnisse
Previous: 7 Ergebnisse
Weil die zur Durchführung von Messungen zur
Verfügung stehenden Kennlinienschreiber für Ströme bis lediglich 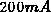 geeignet waren, stand ein vollständiger Satz von Meßkurven nur für
DMOS-Transistoren mit 60 und 80 Zellen zur Verfügung. Von einem
4000zelligen DMOS-Transistor waren lediglich Messungen bei einer
Drainspannung von
geeignet waren, stand ein vollständiger Satz von Meßkurven nur für
DMOS-Transistoren mit 60 und 80 Zellen zur Verfügung. Von einem
4000zelligen DMOS-Transistor waren lediglich Messungen bei einer
Drainspannung von 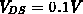 vorhanden (dies ist die übliche
Spannung, um den On-Widerstand zu messen).
vorhanden (dies ist die übliche
Spannung, um den On-Widerstand zu messen).
Die Anpassung der Parameter des DMOS-Modells wurde mit Hilfe des Programms
ICCAP der Firma HP durchgeführt. Dieses Programm erlaubt es neben den
Möglichkeiten, Meßgeräte anzusteuern und die gemessenen Daten
abzuspeichern, über den Aufruf verschiedener externer Programme zur
Netzwerksimulation, Parameteranpassungen durchzuführen. Als Algorithmus
wird ein für solche Probleme standardmäßig eingesetztes
Marquard-Levenberg Verfahren [76] verwendet.
Als externes Netzwerksimulationsprogramm wird auch SABER unterstützt.
Im Falle einer Parameteroptimierung wird nun der Netzwerksimulator vom
in ICCAP implementierten Optimierungsalgorithmus mehrmals aufgerufen, und
die zur Optimierung freigegeben Modellparameter werden angepaßt. ICCAP
erzeugt die für den jeweiligen Aufruf notwendigen Eingabedaten für den
Netzwerksimulator, startet diesen und verarbeitet dessen Ausgabedaten. Diese
sehr flexible Lösung (es werden die wichtigsten Schaltungssimulatoren
unterstützt) hat allerdings den Nachteil, daß sie aufgrund des mit dem
Aufruf des externen Netzwerksimulators verbundenen ,,Overheads`` relativ
langsam ist. Für einen Optimierungslauf ist das Netzwerksimulationsprogramm
i.a. sehr häufig aufzurufen.
An den Transferkennlinien eines 80zelligen DMOS-Transistors wurden zuerst
die Einsatzspannung, die Sättigungsgeschwindigkeit und die
Nullfeldbeweglichkeit der Elektronen im Kanal, der Drainwiderstand und die
pinch-off-Spannung des JFETs angepaßt. Außerdem wurden die Parameter,
die den Unterschwellenbereich und den Übergang zu diesem beschreiben,
optimiert. Nachdem dadurch eine zufriedenstellende Übereinstimmung erreicht
worden war, wurde eine globale Anpassung aller Fit- und physikalischen
Parameter, deren Werte nicht exakt bekannt sind, durchgeführt.
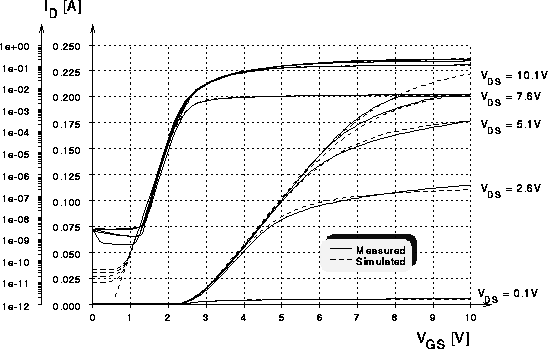
Abbildung 7.1: Transferkennlinien eines DMOS-Transistors
mit 80 Zellen in linearer und logarithmischer Darstellung.
Die angepaßten Kurven (siehe Abb. 7.1) weisen eine maximale
Abweichung von 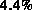 und eine mittlere quadratische Abweichung von
und eine mittlere quadratische Abweichung von  auf. In der logarithmischen Darstellung erkennt man die gute
Übereinstimmung im Übergangsbereich zwischen starker und schwacher
Inversion und im Bereich unterhalb der Schwellspannung (schwache Inversion).
In allen folgenden Simulationen wird ausschließlich der an diesen Messungen
bestimmte Parametersatz verwendet, es werden lediglich die drei Parameter
für die Skalierbarkeit entsprechend der Zellenzahl verändert (siehe
Abschnitt 6.7.1).
auf. In der logarithmischen Darstellung erkennt man die gute
Übereinstimmung im Übergangsbereich zwischen starker und schwacher
Inversion und im Bereich unterhalb der Schwellspannung (schwache Inversion).
In allen folgenden Simulationen wird ausschließlich der an diesen Messungen
bestimmte Parametersatz verwendet, es werden lediglich die drei Parameter
für die Skalierbarkeit entsprechend der Zellenzahl verändert (siehe
Abschnitt 6.7.1).
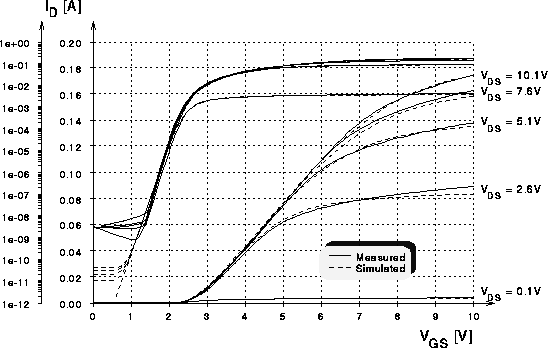
Abbildung 7.2: Transferkennlinien eines DMOS-Transistors
mit 60 Zellen in linearer und logarithmischer Darstellung.
Abb. 7.2 zeigt die Transferkennlinien für einen DMOS-Transistor mit
60 Zellen. Obwohl, wie erwähnt, auf diese Meßkurven keine Anpassung
erfolgte, ergibt sich eine ebenso gute Übereinstimmung wie für den
DMOS-Transistor mit 80 Zellen. Dies zeigt, daß die Skalierbarkeit im
Bereich kleiner Zellenzahlen, wo der Anteil der Randzellen hoch ist und sich
bei Änderung der Zellenzahlen relativ stark ändert, gut funktioniert.
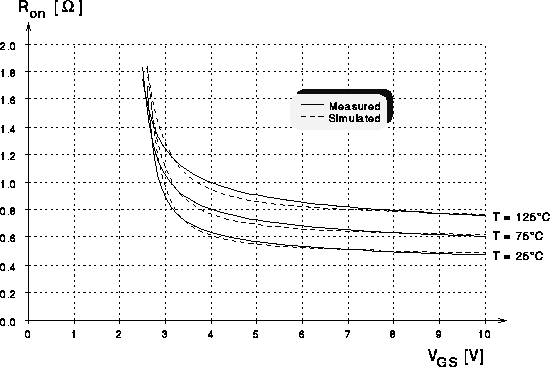
Abbildung 7.3: On-Widerstand eines DMOS-Transistors
mit 4000 Zellen fuer 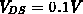 bei verschiedenen Temperaturen.
bei verschiedenen Temperaturen.
Daß die Skalierbarkeit aber auch für große Zellenzahlen sehr gut
ist, zeigen Abb. 7.3 und Abb. 7.4. Der On-Widerstand im Bereich
der Schwellspannung und darüber für verschiedene fest eingeprägte
Meßtemperaturen ist für einen DMOS-Transistor mit 4000 Zellen
in Abb. 7.3 gezeigt. Wie zu erwarten, steigt der
On-Widerstand mit zunehmender Temperatur an. Das ist leicht aus der
geringeren Beweglichkeit der Elektronen im Driftgebiet aufgrund steigender
thermischer Gitterschwingungen erklärbar. Dieser Effekt wird u.a. durch
die Temperaturabhängigkeit der Beweglichkeit im Modell des Drainwiderstands
im subcircuit-Modell angenähert (vgl. Abschnitt 6.7.2).
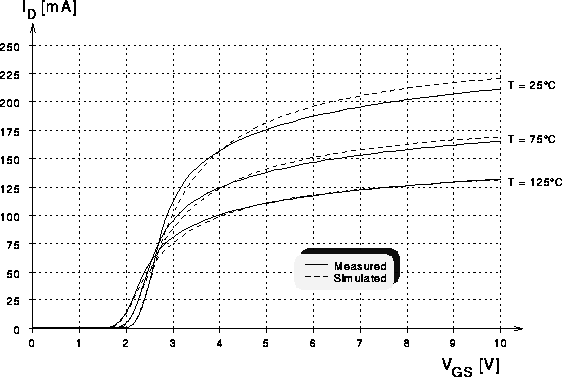
Abbildung 7.4: Transferkennlinien eines DMOS-Transistors mit 4000 Zellen fuer 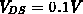 bei verschiedenen Temperaturen.
bei verschiedenen Temperaturen.
Aber auch ein weiterer wichtiger Temperatureffekt, die Verschiebung der
Einsatzspannung, ist an den Messungen der Transferkennlinien am
4000zelligen DMOS-Transistor
deutlich zu erkennen (siehe Abb. 7.4). Die temperaturabhängigen
Beiträge zur Einsatzspannung sind das Fermipotential im 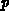 -body
-body
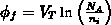 und die
Flachbandspannung
und die
Flachbandspannung  [6][57]. Beide Größen nehmen
mit steigender Temperatur ab. Es ergibt sich eine in weitem Bereich linear
temperaturabhängige Einsatzspannung. Dieser Effekt wird gut durch das
Modell beschrieben.
[6][57]. Beide Größen nehmen
mit steigender Temperatur ab. Es ergibt sich eine in weitem Bereich linear
temperaturabhängige Einsatzspannung. Dieser Effekt wird gut durch das
Modell beschrieben.
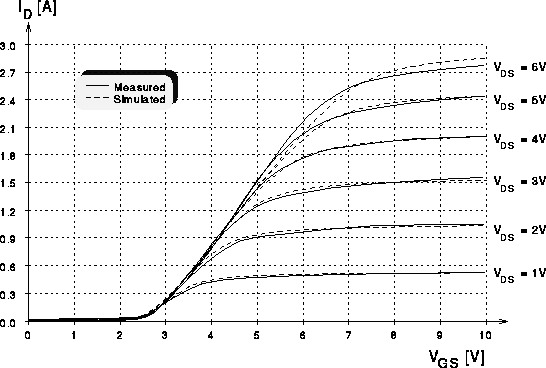
Abbildung 7.5: Transferkennlinien eines DMOS-Transistors
mit 1800 Zellen.
Um die Skalierbarkeit überprüfen zu können, ist es notwendig, das Modell
auch für größere Zellenzahlen und bei höheren Drainspannungen mit
Messungen zu vergleichen. Das Problem des niedrigen Maximalstroms der zur
Verfügung stehenden Kennlinienschreiber konnte durch folgende Anordnung
umgangen werden: Mit Hilfe eines
Speicheroszilloskops, einer steifen Spannungsquelle und eines
Funktionsgenerators kann eine quasistatische Transferkennlinie
aufgenommen werden. An den Drainkontakt wird die Spannungsquelle
angeschlossen, an den Eingang ein ,,langsames`` Dreiecksignal angelegt, wobei
zwischen den einzelnen Dreieckpulsen große Intervalle liegen, damit sich
das Bauelement nicht aufheizen kann.
Die für die einzelnen Drainspannungen aufgenommenen Kurven werden aus dem
Speicheroszilloskop ausgelesen und sind in Abb. 7.5 zusammen mit den
simulierten Kurven dargestellt. Man sieht, daß die gemessenen und
simulierten Kurven eines DMOS-Transistors mit 1800 Zellen gut
übereinstimmen. Hier wurden dieselben Parameter verwendet wie für den 60-
und 80zelligen DMOS-Transistor. Die Skalierbarkeit erstreckt sich also über
weite Bereiche. Sie verliert lediglich für sehr geringe Zellenzahlen, so
insbesondere für einen Einzeller, ihre Gültigkeit. Dafür muß ein eigens
bestimmter Parametersatz verwendet werden.
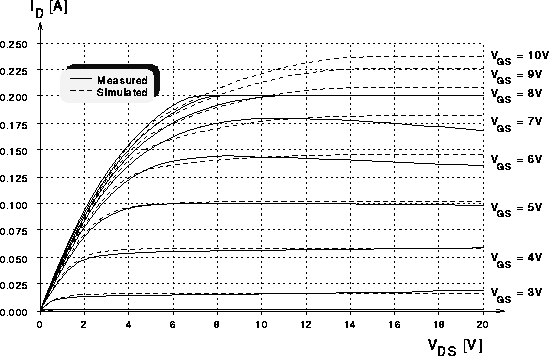
Abbildung 7.6: Ausgangskennlinien eines DMOS-Transistors
mit 80 Zellen.
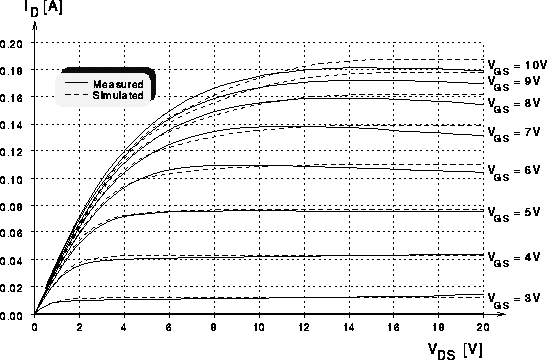
Abbildung 7.7: Ausgangskennlinien eines DMOS-Transistors
mit 60 Zellen.
Die Abbildungen 7.6 und 7.7 zeigen die Ausgangskennlinien
des DMOS-Transistors mit 80 bzw. 60 Zellen. In den gemessenen
Ausgangskennlinien sind negative differentielle Ausgangsleitwerte zu sehen.
Dies ist ein typischer Temperatureffekt, der bei Messung relativ hoher
Ströme durch Eigenerwärmung (im Gegensatz zu den bei den Messungen des
DMOS-Transistors mit 4000 Zellen eingeprägten Meßtemperaturen) auftritt.
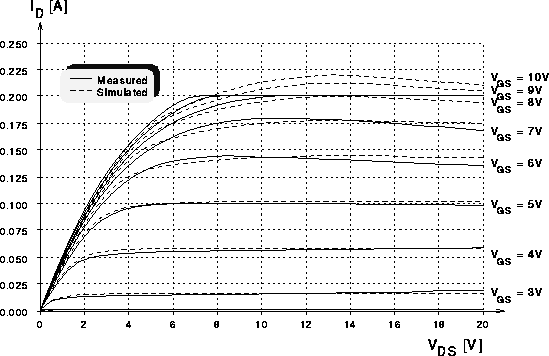
Abbildung 7.8: Ausgangskennlinien eines DMOS-Transistors mit 80 Zellen bei Berücksichtigung der Eigenerwärmung im DMOS-Modell.
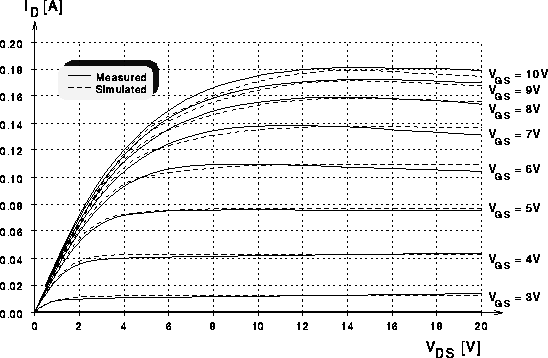
Abbildung 7.9: Ausgangskennlinien eines DMOS-Transistors mit 60 Zellen bei Berücksichtigung der Eigenerwärmung im DMOS-Modell.
Die Abbildungen 7.8 und 7.9 zeigen die Ausgangskennlinien
bei Berücksichtigung der Eigenerwärmung im DMOS-Modell (bei den Kurven in
den Abbildungen 7.6 und 7.7 war dieses Modul des
subcircuit-Modells ausgeschaltet). Man sieht, daß die Eigenerwärmung
bzw. ihre Auswirkung auf die Kennlinien mit dem einfachen implementierten
Modell nicht für alle Gatespannungswerte eine gute Übereinstimmung bringt.
Das implementierte Modell für die Eigenerwärmung des DMOS-Transistors
dürfte etwas zu einfach sein, um diesen Effekt über alle Spannungsbereiche
richtig beschreiben zu können.
Als AC-Messungen standen lediglich Kurven für den 60- und 80zelligen
DMOS-Transistor zur Verfügung. Diese Messungen waren als Brückenmessungen
und demnach mit verschwindender Drainspannung
durchgeführt worden. Für Messungen für verschiedene Werte von 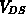 wären aufwendigere
wären aufwendigere 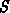 -Parameter-Messungen notwendig gewesen. Für
Transistoren mit höheren Zellenzahlen standen keine Eichstrukturen zur
Verfügung, aus denen parasitäre Kapazitäten, die die Messung
verfälschen, zur Korrektur der AC-Messungen gewonnen werden können.
-Parameter-Messungen notwendig gewesen. Für
Transistoren mit höheren Zellenzahlen standen keine Eichstrukturen zur
Verfügung, aus denen parasitäre Kapazitäten, die die Messung
verfälschen, zur Korrektur der AC-Messungen gewonnen werden können.
Bei der Anpassung der Kapazitätskurven ist lediglich der Parameter, der die
Aufteilung der Gate-Drain-Kapazität auf die Knoten 1 und 2 (siehe
Abb. 6.1) festlegt, zu bestimmen. Auf eine Anpassung der
overlap-Kapazitäten des Kanal-MOSFET-Modells braucht kein großer
Wert gelegt zu werden, da sie betragsmäßig sehr klein im Vergleich zu den
Gesamtkapazitäten des DMOS-Transistors sind.
Die Abbildungen 7.10 und 7.11 zeigen den Vergleich der
gemessenen Eingangskapazität 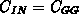 und ihre Aufteilung in
und ihre Aufteilung in
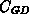 und
und 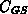 mit dem expliziten Kapazitätsmodell. Man sieht, daß
sich eine gute Übereinstimmung nur für positive Gatespannungen ergibt,
meist ist dies aber gerade jener Bereich, in dem die Kapazitäten im Modell
wirklich gebraucht werden. Zwischen
mit dem expliziten Kapazitätsmodell. Man sieht, daß
sich eine gute Übereinstimmung nur für positive Gatespannungen ergibt,
meist ist dies aber gerade jener Bereich, in dem die Kapazitäten im Modell
wirklich gebraucht werden. Zwischen 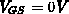 und der Schwellspannung
ist die Übereinstimmung für
und der Schwellspannung
ist die Übereinstimmung für 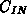 und
und 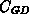 nicht sehr gut. Dies
liegt an der (auch bei Standard-AC-Modellen für MOSFETs festzustellenden)
mangelhaften Modellierung der Kapazitäten im Übergang zwischen Verarmungs-
und Akkumulationsbereich (siehe auch Abschnitt 6.3.3.4). Die
Aufteilung auf
nicht sehr gut. Dies
liegt an der (auch bei Standard-AC-Modellen für MOSFETs festzustellenden)
mangelhaften Modellierung der Kapazitäten im Übergang zwischen Verarmungs-
und Akkumulationsbereich (siehe auch Abschnitt 6.3.3.4). Die
Aufteilung auf 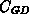 und
und 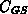 oberhalb der Schwellspannung wird durch
dieses Modell jedoch gut beschrieben (es gibt einen Meßfehler in den
AC-Kurven, da
oberhalb der Schwellspannung wird durch
dieses Modell jedoch gut beschrieben (es gibt einen Meßfehler in den
AC-Kurven, da 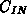 etwas kleiner als die Summe von
etwas kleiner als die Summe von 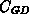 und
und 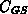 ist).
ist).
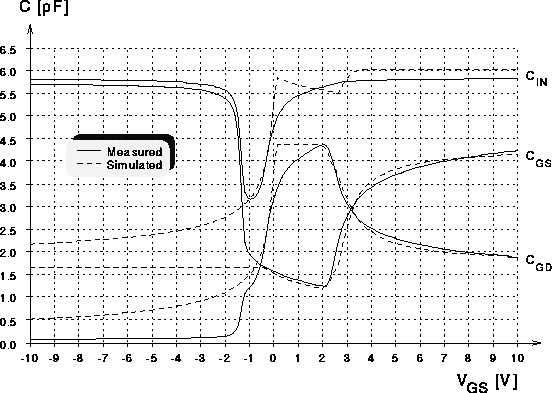
Abbildung 7.10: Kapazitaetskurven eines
DMOS-Transistors mit 80 Zellen bei  (explizites
Kapazitaetsmodell).
(explizites
Kapazitaetsmodell).
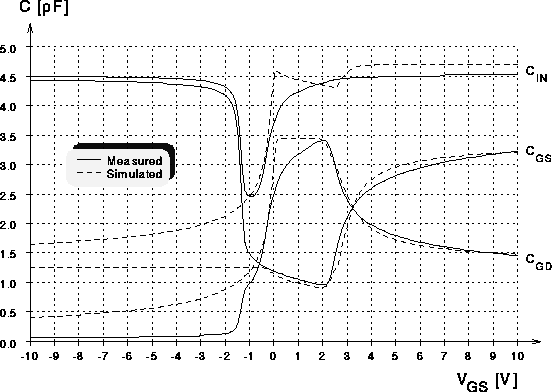
Abbildung 7.11: Kapazitaetskurven eines
DMOS-Transistors mit 60 Zellen bei  (explizites
Kapazitaetsmodell).
(explizites
Kapazitaetsmodell).
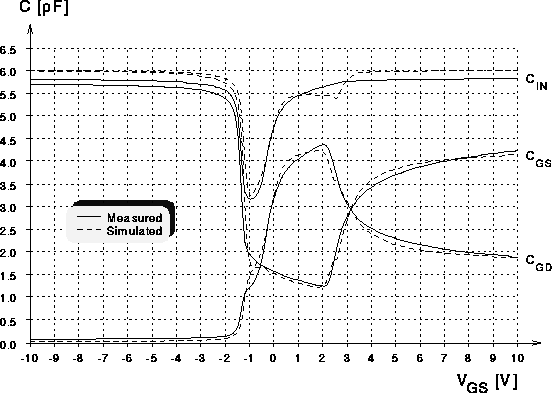
Abbildung 7.12: Kapazitaetskurven eines
DMOS-Transistors mit 80 Zellen bei 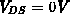 (implizites
Kapazitaetsmodell).
(implizites
Kapazitaetsmodell).
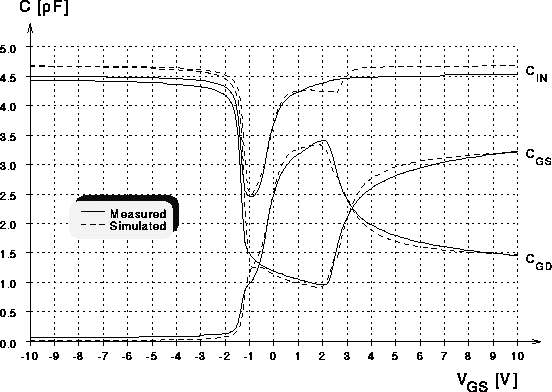
Abbildung 7.13: Kapazitaetskurven eines
DMOS-Transistors mit 60 Zellen bei 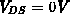 (implizites
Kapazitaetsmodell).
(implizites
Kapazitaetsmodell).
Für das implizite DMOS-Kapazitätsmodell sind die Verläufe in
Abb. 7.12 und Abb. 7.13 dargestellt. Es ergeben sich über alle
Betriebsbereiche des DMOS-Transistors sehr gute Übereinstimmungen zwischen
gemessenen und simulierten Kurven. Die Abbildungen 7.10 bis
7.13 zeigen außerdem, daß die Skalierung auch für das
AC-Modell gut funktioniert.




Next: 7.2 DMOS-Schaltungen
Up: 7 Ergebnisse
Previous: 7 Ergebnisse
Martin Stiftinger
Wed Oct 5 11:53:06 MET 1994
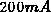 geeignet waren, stand ein vollständiger Satz von Meßkurven nur für
DMOS-Transistoren mit 60 und 80 Zellen zur Verfügung. Von einem
4000zelligen DMOS-Transistor waren lediglich Messungen bei einer
Drainspannung von
geeignet waren, stand ein vollständiger Satz von Meßkurven nur für
DMOS-Transistoren mit 60 und 80 Zellen zur Verfügung. Von einem
4000zelligen DMOS-Transistor waren lediglich Messungen bei einer
Drainspannung von 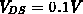 vorhanden (dies ist die übliche
Spannung, um den On-Widerstand zu messen).
vorhanden (dies ist die übliche
Spannung, um den On-Widerstand zu messen).





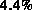 und eine mittlere quadratische Abweichung von
und eine mittlere quadratische Abweichung von 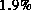 auf. In der logarithmischen Darstellung erkennt man die gute
Übereinstimmung im Übergangsbereich zwischen starker und schwacher
Inversion und im Bereich unterhalb der Schwellspannung (schwache Inversion).
In allen folgenden Simulationen wird ausschließlich der an diesen Messungen
bestimmte Parametersatz verwendet, es werden lediglich die drei Parameter
für die Skalierbarkeit entsprechend der Zellenzahl verändert (siehe
Abschnitt
auf. In der logarithmischen Darstellung erkennt man die gute
Übereinstimmung im Übergangsbereich zwischen starker und schwacher
Inversion und im Bereich unterhalb der Schwellspannung (schwache Inversion).
In allen folgenden Simulationen wird ausschließlich der an diesen Messungen
bestimmte Parametersatz verwendet, es werden lediglich die drei Parameter
für die Skalierbarkeit entsprechend der Zellenzahl verändert (siehe
Abschnitt 


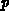 -body
-body
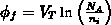 und die
Flachbandspannung
und die
Flachbandspannung 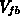





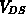 wären aufwendigere
wären aufwendigere 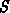 -Parameter-Messungen notwendig gewesen. Für
Transistoren mit höheren Zellenzahlen standen keine Eichstrukturen zur
Verfügung, aus denen parasitäre Kapazitäten, die die Messung
verfälschen, zur Korrektur der AC-Messungen gewonnen werden können.
-Parameter-Messungen notwendig gewesen. Für
Transistoren mit höheren Zellenzahlen standen keine Eichstrukturen zur
Verfügung, aus denen parasitäre Kapazitäten, die die Messung
verfälschen, zur Korrektur der AC-Messungen gewonnen werden können.
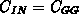 und ihre Aufteilung in
und ihre Aufteilung in
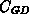 und
und 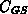 mit dem expliziten Kapazitätsmodell. Man sieht, daß
sich eine gute Übereinstimmung nur für positive Gatespannungen ergibt,
meist ist dies aber gerade jener Bereich, in dem die Kapazitäten im Modell
wirklich gebraucht werden. Zwischen
mit dem expliziten Kapazitätsmodell. Man sieht, daß
sich eine gute Übereinstimmung nur für positive Gatespannungen ergibt,
meist ist dies aber gerade jener Bereich, in dem die Kapazitäten im Modell
wirklich gebraucht werden. Zwischen 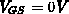 und der Schwellspannung
ist die Übereinstimmung für
und der Schwellspannung
ist die Übereinstimmung für 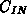 und
und 
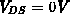 (explizites
Kapazitaetsmodell).
(explizites
Kapazitaetsmodell).

