List of Figures

• 1.1. Copper dual-damascene fabrication process. subfig1:DD_a Via patterning. subfig1:DD_b Via and trench patterning. subfig1:DD_c Barrier layer deposition and Cu seed deposition. subfig1:DD_d Cu electroplating and excess removal by chemical mechanical polishing. subfig1:DD_e Capping layer deposition.
• 1.2. Failures in a damascene line. subfig1:fast_failure Failure dominated by the void nucleation phase. subfig1:slow_failure Failure dominated by void nucleation migration and growth.
• 1.3. EM lifetime variation as a function of the interconnect dimensions. This curve is calculated based on equation (1.13).
• 1.4. Extraction of activation energy and current density exponent from EM tests. subfig1:Black_Ea Activation energy calculation. subfig1:Black_n Current density exponent determination.
• 1.5. Void growth in a single-damascene copper interconnect.
• 1.6. Schematic design of a TCAD tool for EM simulation.
• 2.1. Stress build-up at 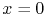$x=0$ according to Korhonen's model.
• 2.2. Stress build-up along the interconnect at different times.
• 2.3. Homogeneous nucleation rate dependence on temperature and hydrostatic stress. The nucleation rate is small, even at high temperatures and stresses.
• 2.4. Schematic void nucleation at an interface site of weak adhesion.
• 3.1. Dual-damascene interconnect structure.
• 3.2. Effect of a vacancy in an ideal crystal lattice. subfig3:perfect_lattice Initial lattice. subfig3:deformed_lattice Deformed lattice.
• 3.3. Grain boundary model.
• 3.4. Interface model.
• 4.1. Finite element mesh of a three-dimensional interconnect structure discretized with tetrahedrons.
• 4.2. Tetrahedral finite element. subfig4:tetrahedron_xyz Original coordinate system. subfig4:tet_transformed Transformed coordinate system.
• 4.3. Simulation procedure of electromigration in FEDOS.
• 4.4. Mesh refinement at a grain boundary and at a material interface.
• 5.1. Detail of the vacancy distribution next to the cathode end of the line after 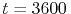$t=3600\,$s (in cm$^{-3}$).
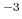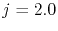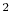• 5.2. Vacancy concentration along the line at different times for $\symCurrDens=2.0$ MA/cm$^2$. The symbols are the numerical simulation results and the solid lines are obtained by (5.2).
• 5.3. Vacancy concentration development at 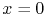$x=0$ for different magnitudes of current density. The symbols are the numerical simulation results and the solid lines are obtained by (5.2).
• 5.4. The intersection of two copper grains with different properties forming a grain boundary.
• 5.5. Detail of the vacancy concentration at the grain boundary formed by the intersection of two grains with different diffusion coefficients (in cm$^{-3}$).
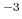• 5.6. Vacancy concentration at the grain boundary for different vacancy relaxation times. The symbols are the numerical simulation results and the solid lines are obtained by (5.8).
• 5.7. Vacancy concentration at the grain boundary as a function of time. The vacancy relaxation time, 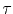$\symVacRelTime$, is a key parameter in determining the magnitude of vacancy supersaturation and the time to reach the steady state.
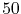
• 5.8. Hydrostatic stress distribution in a 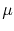$50$ $\mu$m long line at 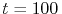$t = 100\,$h (in MPa). subfig5:K_stress_cathode Tensile stress (positive) develops at the cathode end of the line. subfig5:K_stress_anode At the anode end compressive stress (negative) develops.
• 5.9. Stress profile along the line at different periods in time.
• 5.10. Vacancy concentration as a function of time at the cathode end of the line.
• 5.11. Stress evolution during the quasi steady state period. In this period the stress grows linearly with time.
• 5.12. Stress build-up with time. A non-linear increase of stress is observed at longer times.
• 5.13. Complete dual-damascene interconnect via.
• 5.14. Stress components along the upper line, via, and lower line.
• 5.15. Hydrostatic stress distribution in an interconnect via after cooling from 500 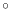$^{\circ }$C to 100 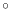$^{\circ }$C (in MPa). subfig5:Aniso_HydStress_grid Distribution on the mesh nodes. subfig5:Aniso_HydStress_cut Profile in a cut through the structure.
• 5.16. Vacancy distribution at the upper line. Vacancies concentrate at the bottom of the via, which is a blocking boundary for vacancy diffusion (in cm$^{-3}$).
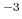• 5.17. Vacancy evolution at the bottom of the via. Three cases are studied: constant diffusivity, hydrostatic stress dependent diffusivity, and stress tensor dependent diffusivity.
• 5.18. Electric potential along the interconnect line (in V).
• 5.19. Current density distribution next to the via region (in MA/cm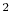$^2$). The current density magnitude is larger in the via than in the line, since the cross section of the via is smaller than that of the line.
• 5.20. Detail of the temperature distribution in the via region through a cut along the 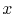$x$ coordinate. A very small temperature increase in the via is caused by a higher joule heating in this region (in K).
• 5.21. Vacancy distribution in the M2 line and via after 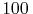$100\,$h of electromigration test (in cm$^{-3}$).
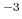• 5.22. Stress distribution in the via region through a cut along the 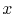$x$ coordinate after 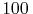$100\,$h of electromigration test (in MPa).
• 5.23. Vacancy distribution in the M1 line (downstream case) at 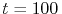$t = 100\,$h (in cm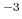$^{-3}$). Vacancies concentrate right underneath the via.
• 5.24. Hydrostatic stress due to downstream electromigration at 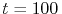$t = 100\,$h (in MPa). The maximum stress is located right under the via.
• 5.25. Vacancy concentration, when the copper/capping layer interface is treated as a fast diffusivity path (in cm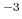$^{-3}$). Vacancies concentrate at the copper/capping layer interface at the cathode end of the line.
• 5.26. The peak of hydrostatic stress is located at the copper/capping layer interface, when this interface acts as a fast diffusivity path (in MPa).
• 5.27. Vacancy distribution for the downstream case (in cm$^{-3}$).
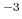• 5.28. Hydrostatic stress distribution (in MPa). The peak of the stress is shifted to the left edge of the via, where copper, capping, and barrier layer intersect.
• 5.29. Interconnect structure with redundant via.
• 5.30. Vacancy distribution in the double via structure (in cm$^{-3}$).
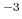• 5.31. Hydrostatic stress under the vias in a double via structure (in MPa). The stress peak is located under the outer via at the intersection between copper, capping layer, and barrier layer.
• 5.32. Maximum hydrostatic stress build-up under the outer via as a function of the distance between the vias for a constant voltage applied at the terminals of the interconnect.
• 5.33. Stress development under the outer via for a constant current applied to the interconnect.
• 5.34. Maximum hydrostatic stress under the outer and inner via as a function of the distance between the vias. The stress for the single via case is given at zero distance between the vias.
• 5.35. Typical microstructure generated from the procedure described above. The grain sizes follow a lognormal distribution, and the angles of the grain boundaries in relation to the top line surface follow a normal distribution.
• 5.36. Schematic simulation procedure.
• 5.37. Vacancy distribution in a bamboo-like interconnect line (in cm$^{-3}$).
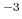• 5.38. Trapped vacancy concentration (in cm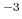$^{-3}$). Vacancies are trapped at grain boundaries, once the vacancy concentration within a grain boundary exceeds the equilibrium value.
• 5.39. Hydrostatic stress distribution in a simulated interconnect (in MPa). Mechanical stress develops at grain boundaries as a result of vacancy trapping/release events.
• 5.40. Peak of hydrostatic stress development for the set with grain size standard deviation of 0.3.
• 5.41. Electromigration lifetime distributions.
• 5.42. Electromigration lifetime standard deviation for different standard deviations of grain size.