(image) (image) [Previous] [Next]

Degradation of Electrical Parameters of Power Semiconductor Devices – Process Influences and Modeling

4.4 Assessment of the extrapolation model

The model for the increase of the device temperature with power supplied to the heater proposed above must be validated. Within the range of the temperature of the thermal chuck the approach can be tested experimentally. Outside this range the extrapolation can be compared to thermal FEM simulations which are capable of handling non-linear thermal resistances. Such simulations give an approximate temperature distribution by transferring the partial differential heat equation to linear equations and solving them numerically.

4.4.1 Experimental

Within the chuck temperature range the extrapolation methods (4.7) and (4.8) can be compared with experimental data as shown in Fig. 4.9.

(image)

Fig. 4.9: Measured rise of the device temperature with poly-heater power supply in the temperature range of the thermal chuck (symbols) for several (math image) [PobegenTDMR13]. The lines are the estimations of (math image) for linear (4.8) and exponential (4.7) extrapolation.

The exponential extrapolation method can correctly capture the increase of the device temperature with heater power. In order to resolve the correctness of the approach better, Fig. 4.10 shows the relative error of the two methods over the switched temperature range.

(image)

Fig. 4.10: Relative error of the linear (4.8) and exponential (4.7) extrapolation method within the chuck temperature range [PobegenTDMR13].

The error of the linear method rises with temperature difference while the error of the exponential method stays below a few percent.

The exponential extrapolation method includes the thermal resistance between the wafer and the chuck or between the die and the package. Consequently, the method can also be used to estimate the temperature of a device which is thermally decoupled from a heat sink. This allows reaching even higher temperatures in the device because only the inefficient mechanisms radiation and convection cause a reduction of the device temperature. For wafer tests thermal decoupling can be achieved by placing the wafer on a plastic layer or by inserting small area spacers between the wafer and the chuck. This approach considerably increases the accessible temperature range, as shown in Fig. 4.11.

(image)

Fig. 4.11: Device temperature increase with heater power for a device on a wafer separated from the chuck by a 2 mm thick plastic board or 4 mm of air. The time until thermal equilibrium is reached is considerably longer than in the presence of a heat sink. For the uppermost line a wait time of 60 s per step is needed. Symbols are measurement data and the lines are the model.

Consequently, also semiconductor materials which have a low thermal resistivity, as e.g. four layer hexagonal SiC (4H-SiC), which has about 40 % of the thermal resistivity of Si, can be operated at high temperatures with the poly-heater.

4.4.2 Thermal simulations

In a first attempt to model the increase of the device temperature with the power supplied to the poly-heater a two-dimensional (2D) thermal model was created using the commercially available analysis system (Ansys) FEM software by Ansys Incorporated. With this model an overall match with experimental data as shown in Fig. 4.12 could only be obtained by arbitrarily changing the thermal conductivity of the Si substrate and its temperature dependence.

(image)

Fig. 4.12: Comparison of a 2D thermal simulation with Ansys with the rise of (math image) with heater power. The original temperature dependent thermal conductivity values of the materials of the model cannot capture the dependence. Only by changing the material parameters arbitrarily a good match can be obtained.

The extrapolation of such a simulation to high temperatures is not of particular interest because it is mostly determined by the effective thermal conductivity at high temperatures. That is to say, the simulation depends on the same assumptions as the exponential extrapolation method which should be tested. In order to exempt the simulation from the same assumptions a 3D model was implemented where both the current through the heater and the heat spread was calculated [PobegenTDMR13]. For this model the structure as sketched in Fig. 4.1 was simplified by omitting the metal wires. Consequently, the model consists basically of two bricks of poly surrounded by SiO2 , and situated on a large block of Si.

To correctly capture the poly-heater behavior, the poly lines were simulated electrically and thermally. For the other materials of the model it was sufficient to perform only a thermal simulation, i.e. no electrical device simulation was conducted. The temperature dependent electrical resistivity of the poly was obtained on a dedicated test structure on the same wafer. The temperature dependent thermal resistivity of the Si substrate was measured externally on an unprocessed raw wafer with a calibrated differential scanning calorimetry equipment. The value of the thermal resistivity is rather large compared to standard Si [Let+87; GS64] because of the high doping level of the substrate [Sla64; LA05], needed to reduce the on-resistance of vertical power devices residing on the same wafer. The temperature dependence of the thermal resistivity could be modeled better with a power law coefficient of \( 1 \), instead of the suggested coefficient of \( 1.324 \) [Let+87]. Also, a cross check of the change of the simulation result with a modification of the power law coefficient between \( 0.6 \) and \( 1.2 \) showed vanishing influence. That is to say, in a small range the particular choice of the power law coefficient is rather irrelevant and \( \gls {Rth} \propto \gls {T} \) eases the calculations considerably.

The model has Neumann boundary conditions at all borders except at the bottom surface. Those boundaries act as adiabatic boundaries meaning that heat flow through the boundary is prohibited. At the bottom a phenomenological layer was introduced which accounts for the thermal behavior of the interface between the wafer and the chuck [PobegenTDMR13; CS01; IR05]. This layer is 20 µm thick and has a thermal conductivity of 0.5 W/(m K). The bottom surface of this interface layer was set to Dirichlet boundary conditions with the temperature of the chuck. A \(4x4\) mm large Si block was needed to account for the large lateral heat spread visible in an increase of the surface temperature at the outer boundaries. The device temperature was determined by averaging the temperature of the Si substrate near the interface to the SiO2 at the exact position of the device.

In Fig. 4.13 a comparison between the simulation result and the exponential extrapolation method is shown.

(image)

Fig. 4.13: Extrapolation of the device temperature for large heater power and high chuck temperatures [PobegenTDMR13]. Both the 3D electrothermal Ansys simulation and the exponential extrapolation method (4.7) give equivalent results in the temperature range above the highest chuck temperature of 200 °C.

The 3D FEM simulation tends to overestimate the device temperature slightly. This might be due to the fact that, even though the exact dimensions of the heater structure and accurate material parameters were simulated, possible cooling parts were neglected. These are especially the power metal pads for device contact and the reduction of the actual wafer diameter from 200 mm to a \(4x4\) mm block.

The equivalent behavior of the extrapolation using (4.7) and the 3D simulation shows that the reduction to a 1D problem is a valid approach for the poly-heater structure [PobegenTDMR13].

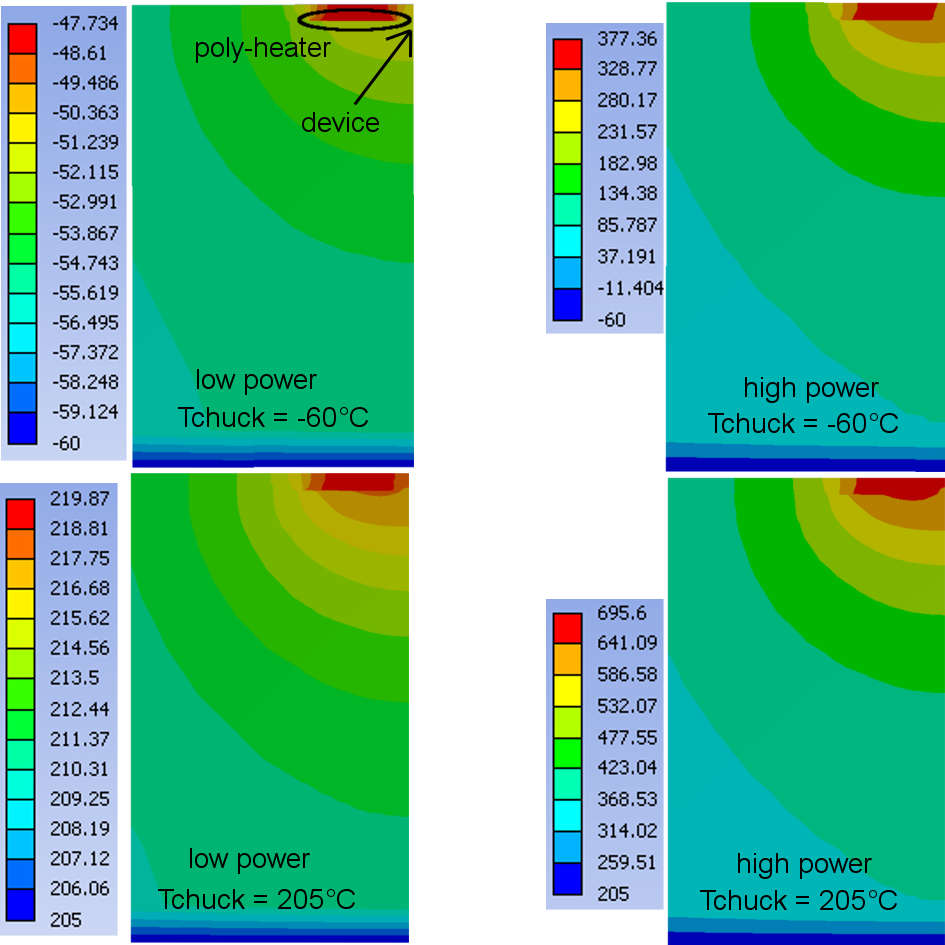
Furthermore, the simulation allows investigating the reason for the equivalence of \( \gls {Rthsub}(\gls {Tdev}) \) and \( \gls {Rthsub}(\gls {Tchuck}) \). As shown in Fig. 4.14, during poly-heater use (high heater supply power) as well as during calibration (low heater power) approximately the same relative temperature distributions occur.

(image)

Fig. 4.14: Cross sections of the temperature distributions in the center of a poly-heater device [PobegenTDMR13]. Illustrated are two different chuck temperatures and two different power supply values. Only the central region of the device/poly-heater structure is shown.

The region of the highest temperature is always very close to the device. Since the (math image) of the substrate increases with temperature the same region is responsible for the thermal resistance. Consequently, the thermal resistance of the substrate is determined by the bottleneck region with the highest temperature close to the device and both approaches to measure the thermal resistance give equivalent results.