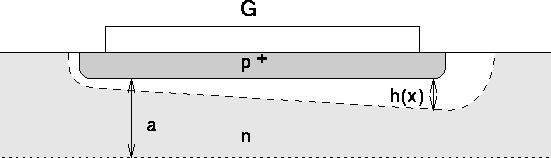
Abbildung 6.11: Weite der Depletionszone in einem JFET.




Wie die Bauelementsimulationen in Abschnitt 5.3 gezeigt haben, ist das Stromflußgebiet in Abhängigkeit der angelegten Spannungen sehr unterschiedlich. Speziell im Gebiet der Sättigung kann sich für höhere Drainspannungen von der Mitte der Grenzfläche der Driftzone zum Gateoxid zwischen zwei benachbarten Zellen eine Raumladungszone ausbilden. In der Quasisättigung ist diese Raumladungszone für die untersuchte Geometrie nicht zu beobachten. Diese Effekte sind aber natürlich auch geometrieabhängig. Die sehr komplexen Abhängigkeiten physikalisch fundiert in analytischer Form beschreiben zu wollen, ist nicht realistisch. Der in [90] unternommene Versuch ergibt trotz der nicht unwesentlichen Vernachlässigungen recht komplizierte Formeln. Außerdem geht er davon aus, daß sich zwischen Akkumulations- und JFET-Gebiet ein Minimum im Potentialverlauf ergibt. Dies ist nun bei geringen Gatespannungen (im Bereich der Sättigung) für höhere Drainspannungen nicht immer erfüllt (vgl. Abb. 5.13). Es wird bei diesem Ansatz jener Bereich, in dem sich eine Raumladungszone in der Mitte der Driftzone ausbildet, nicht richtig erfaßt.
Es wurde ein sehr einfacher Ansatz getroffen, der nur prinzipiell die wesentlichsten Effekte berücksichtigt:
Im folgenden soll kurz allgemein ein einfaches JFET-Modell hergeleitet und dann auf das im subcircuit-Modell verwendete übergegangen werden.

Abbildung 6.11: Weite der Depletionszone in einem JFET.
Abb. 6.11 zeigt schematisch einen Ausschnitt aus dem Kanalbereich
eines JFETs. Der Drainkontakt liegt auf der rechten Seite, der Sourcekontakt
auf der linken. Es gilt 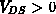 und
und 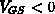 . Die punktierte
Linie soll eine Symmetrieebene andeuten (dieser JFET hat also an der
Unterseite einen zweiten Gatekontakt, der mit dem oberen kurzgeschlossen
ist). Die folgenden Formeln gelten allerdings nur für den abgebildeten
Halbtransistor. Ist wie hier angenommen
. Die punktierte
Linie soll eine Symmetrieebene andeuten (dieser JFET hat also an der
Unterseite einen zweiten Gatekontakt, der mit dem oberen kurzgeschlossen
ist). Die folgenden Formeln gelten allerdings nur für den abgebildeten
Halbtransistor. Ist wie hier angenommen 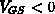 und
und 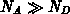 , dann
bildet sich eine Raumladungszone um den metallurgischen
, dann
bildet sich eine Raumladungszone um den metallurgischen  -Übergang
praktisch nur in das
-Übergang
praktisch nur in das  -Gebiet hinein aus (diese ist weiß eingezeichnet).
Für jede Position
-Gebiet hinein aus (diese ist weiß eingezeichnet).
Für jede Position  kann man den Strom anschreiben als:
kann man den Strom anschreiben als:
Mit dem built-in-Potential 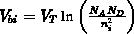 und der pinch-off-Spannung
und der pinch-off-Spannung
(errechnet aus der Bedingung, daß die Weite der Verarmungszone am
drainseitigen Kanalende die Dicke  erreicht:
erreicht:  )
ergibt sich:
)
ergibt sich:
Setzt man diese Beziehung in Gleichung 6.112 ein und integriert diese
Gleichung entlang des Kanals ( ), so erhält man:
), so erhält man:
Aus 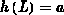 folgt die Sättigungsbedingung
folgt die Sättigungsbedingung 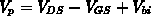 . Damit lauten in der Sättigung:
. Damit lauten in der Sättigung:
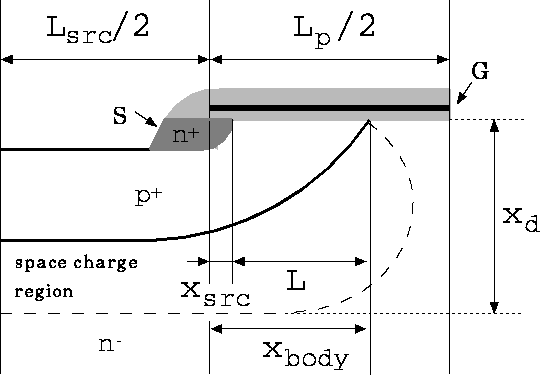
Abbildung 6.12: Charakteristische Abmessungen des
DMOS-Transistors im JFET-Gebiet.
Abb. 6.12 zeigt schematisch eine halbe DMOS-Zelle mit den charakteristischen Abmessungen im JFET-Gebiet. Damit ist in obige Gleichungen einzusetzen:
Die Weite kann man aus dem Quotienten der Fläche des JFET-Gebiets und
 gewinnen. Die Fläche kann man aus
gewinnen. Die Fläche kann man aus 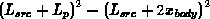 errechnen.
Zusätzlich wird der sehr wichtige Faktor für die
Geschwindigkeitssättigung im JFET-Modell für den DMOS-subcircuit
berücksichtigt. Hier wird ein dem Kanal-Modell ähnlicher Ansatz gewählt:
errechnen.
Zusätzlich wird der sehr wichtige Faktor für die
Geschwindigkeitssättigung im JFET-Modell für den DMOS-subcircuit
berücksichtigt. Hier wird ein dem Kanal-Modell ähnlicher Ansatz gewählt:
Im subcircuit sind statt der Knoten Drain, Source und Gate die Knoten 1, 2 und 3 (siehe Abb. 6.1) zu verwenden.
Da dieses Modell eine wesentliche Vereinfachung gegenüber der
tatsächlichen komplexen Physik in diesem Teil des DMOS-Transistors
darstellt und sich die DMOS-Struktur insbesondere auch dadurch vom
benützten einfachen JFET-Modell unterscheidet, daß der Abstand  von der
Symmetrieebene nicht konstant über die Länge des JFETs ist, hat es sich
als sinnvoll erwiesen, die pinch-off-Spannung nicht aus
Gleichung 6.113 zu errechnen, sondern als Fitparameter zu betrachten.
Allerdings zeigt sich im Vergleich mit den Meßkurven, daß die
Berücksichtigung lediglich der wichtigsten Effekte für die Beschreibung im
Gesamtmodell ausreicht (vgl. Kapitel 7.1).
von der
Symmetrieebene nicht konstant über die Länge des JFETs ist, hat es sich
als sinnvoll erwiesen, die pinch-off-Spannung nicht aus
Gleichung 6.113 zu errechnen, sondern als Fitparameter zu betrachten.
Allerdings zeigt sich im Vergleich mit den Meßkurven, daß die
Berücksichtigung lediglich der wichtigsten Effekte für die Beschreibung im
Gesamtmodell ausreicht (vgl. Kapitel 7.1).



