Characterization of electrically active defects at III-N/dielectric interfaces - Methodologies for electrical characterization of interface defects in GaN–based MIS

« Previous Up Next »Contents
Previous: 2.4 Setup for opto-electrical characterization Top: Home Next: 3.2 Impedance characteristics of GaN/AlGaN MIS structures

3 Methodologies for electrical characterization of interface defects in GaN–based MIS–HEMTs

Small signal investigations allow us to study in detail the behavior of the devices under test, as well as their frequency response. A number of methods based on impedance measurements have been established in the past decades in order to evaluate the density of defects at the interface with the dielectric. We focus on the two most used ones, explain their principle of operation and the approximations used, and we underline their limitations when applied to GaN–based devices. The main factor that makes such methods inaccurate in our case is the presence of the AlGaN layer. We investigate the role of the barrier and show that composite GaN/AlGaN structures require a more complex equivalent circuit model than that of regular MIS devices. Furthermore, we highlight other issues that constitute a challenge for an accurate characterization of MIS structures and MIS–HEMTs, namely hysteresis and the CV curve dependence on the measurement parameters. Finally, we develop two methods to evaluate the defect density based on the threshold voltage shift, applying a combination of small and large signal excitation.

3.1 The main established methods and their limitations

In this section we focus on the most used methods based on impedance measurements for the extraction of the interface defect density. In the first place, we need to develop a model for the small–signal response of a MIS structure. We present an equivalent circuit model, highlighting the assumptions and approximations used in the derivation. Then we describe the Terman and the conductance methods in detail, showing how they are applied to the experimental data and their limitations.

3.1.1 The equivalent circuit model

The model for the interface defects should describe the phenomenological loss of energy due to the trapping of conduction electrons into trap states. In the first place, the defects are effectively centres of charge storage: for this reason, we can associate to them a certain capacitance $C_\mr {it}$ . Furthermore, charge trapping do not follow precisely the AC signal, but it lags behind. The small–signal is a perturbation and the system evolves in time in order to return to equilibrium. This can be modelled with a certain characteristic time constant $\tau _\mr {it}$ . The equivalent circuit model therefore consists of the interface state capacitance in series with a certain resistance $R_\mr {it}$ (series RC circuit), which gives rise to the time constant $\tau _\mr {it}$ given by the product $R_\mr {it} C_\mr {it}$ , as shown in Fig. 3.1a.

The equivalent circuit can be derived in a more rigorous way [63]: we summarize here the most important concepts and we highlight the approximations used. The net current density flowing in the device can be written as

$(3.1) \begin{equation} i (\mr {t}) = q \left [ r_n^c (\mr {t}) - r_n^e (\mr {t}) \right ] \label {rate_eq} \end{equation}$

where $r_n^c$ and $r_n^e$ are the capture and emission rate constants for electrons, respectively. The first assumption is the Shockley–Read–Hall (SRH) model for the rate constants. Originally, this theory has been developed for deep trap states inside a semiconductor, but its validity is here assumed to extended to interface states as well. The rate constants depend on the density of electrons available at the semiconductor surface, $n_\mr {s}$ , the density of traps $N_\mr {it}$ , the Fermi function $f$ and the probability for electron capture $c_n$ and emission $e_n$ as

$(3.2) \begin{equation} r_n^c (\mr {t}) = n_\mr {s} N_\mr {it} c_n \left [ 1 - f (\mr {t}) \right ] \quad \quad \mr {and} \quad \quad r_n^e (\mr {t}) = N_\mr {it} e_n f (\mr {t}). \end{equation}$

In the SRH model it is assumed that the capture and emission probability depend on the energy difference between the trap state and, in the case of electrons, the conduction band edge (this topic is discussed further in Chapter 4). In this case, we consider the interface states to be located at the same energetic position inside the bandgap. We also assume the small–signal approximation to be valid, i.e., to a small variation $\delta \!v$ of the gate voltage around the mean value $v_0$ corresponds a small variation of the Fermi function $f$ and of the surface potential $\phi _\mr {s}$ , according to

$(3.3) \begin{equation} v = v_0 + \delta \!v, \quad \quad f = f_0 + \delta \!f \quad \quad \mr {and} \quad \quad \phi _\mr {s} = \phi _\mr {s,0} + \delta \!\phi _\mr {s}. \end{equation}$

Finally, we assume that thermal equilibrium is reached, therefore the detailed balance equation is valid and we can write the electron emission probability as a function of the capture probability:

$(3.4) \begin{equation} e_n = n_\mr {s} c_n \frac {1 - f_0}{f_0}. \label {theq} \end{equation}$

Manipulating Eq. (3.1) with these conditions, we can write a direct relationship between the net current density and the variation of the surface potential, from which an equation for the admittance of the interface, $Y_\mr {it}$ , can be derived:

$(3.5) \begin{equation} i (\mr {t}) = Y_\mr {it} \: \delta \!\phi _\mr {s} \quad \quad \mr {with} \quad \quad Y_\mr {it} = \frac {1}{R_\mr {it}} + i \omega \;C_\mr {it}. \end{equation}$

The admittance $Y_\mr {it}$ can be modelled with a resistance $R_\mr {it}$ and a capacitance $C_\mr {it}$ in series, as shown in Fig. 3.1a. The response of the interface states is therefore characterized by the time constant $\tau _\mr {it} = R_\mr {it} C_\mr {it}$ .

Figure 3.1: Equivalent circuit model for the admittance of the interface defects (a) and of the full MIS structure (b) in the single–level approximation; generalization to an ensemble of trap states with different energy levels (c) and the model of the measured device impedance (d).

(image) — Figure 3.1: Equivalent circuit model for the admittance of the interface defects (a) and of the full MIS structure (b) in the single–level approximation; generalization to an ensemble of trap states with different energy levels (c) and the model of the measured device impedance (d).

In order to investigate the defects at the interface with the dielectric, we need an equivalent circuit model for the full MIS structure. In the first place, we consider the distribution of charge in the device: the charge present at the gate contact $Q_\mr {gate}$ must be counterbalanced by the charge of the depletion region of the semiconductor $Q_\mr {depl}$ , the charge trapped at the interface $Q_\mr {it}$ and any possible fixed charge $Q_\mr {fixed}$ , according to

$(3.6) \begin{equation} - Q_\mr {gate}= Q = Q_\mr {depl} + Q_\mr {it} + Q_\mr {fixed}. \label {chargeMIS} \end{equation}$

When the small signal is applied, only the quantities depending on the surface potential follow the bias oscillation. For this reason, the small–signal current density arises from the contribution of the depletion region, $i_\mr {depl} (\mr {t})$ , and that of the interface, $i_\mr {it} (\mr {t})$ . The former can be written as

$(3.7) \begin{equation} i_\mr {depl} (\mr {t}) = \frac {\mr {d}Q_\mr {depl} (\mr {t})}{\mr {dt}} = \frac {\mr {d}Q_\mr {depl} (\mr {t})}{\mr {d} \phi _\mr {s}} \: \frac {\mr {d}\phi _\mr {s} (\mr {t})}{\mr {dt}} = C_\mr {diel}\: \frac {\mr {d}\phi _\mr {s} (\mr {t})}{\mr {dt}} = i \omega \, C_\mr {diel} \;\delta \!\phi _\mr {s} \end{equation}$

and we have just derived an expression for the latter, $i_\mr {it} (\mr {t}) = Y_\mr {it} \: \delta \!\phi _\mr {s}$ . Together, the small–signal current due to the variation of the surface potential is

$(3.8) \begin{equation} i (\mr {t}) = i_\mr {depl} (\mr {t}) + i_\mr {it} (\mr {t}) = \left [ Y_\mr {it} + i \omega \, C_\mr {diel} \right ] \delta \!\phi _\mr {s}, \end{equation}$

which corresponds to an equivalent circuit model of the depletion capacitance in parallel with the admittance of the interface states. As a second step, we consider the potential drop across the MIS structure. The small–signal bias applied to the gate, $v (\mr {t})$ , is distributed in the semiconductor and the dielectric according to

$(3.9) \begin{equation} v (\mr {t}) = v_0 + \delta \!v = \frac {Q (\mr {t})}{C_\mr {diel}} + \phi _\mr {s} (\mr {t}). \label {this} \end{equation}$

We can evaluate the variation due to the small–signal by taking the time derivative of Eq. (3.9):

$(3.10) \begin{equation} \frac {\mr {d}v (\mr {t})}{\mr {dt}} = i \omega \; \delta \!v = \frac {i (\mr {t})}{C_\mr {diel}} + i \omega \;\delta \!\phi _\mr {s} \end{equation}$

from which we can write

$(3.11) \begin{equation} \delta \!v (\mr {t})= \left [ \frac {1}{Y_\mr {it} + i \omega \;C_\mr {depl}} + \frac {1}{i \omega \;C_\mr {diel}} \right ] i (\mr {t}). \end{equation}$

The model of the full MIS device is therefore the parallel circuit of the depletion capacitance and the admittance of the interface states, in series with the dielectric capacitance. This is illustrated in Fig. 3.1b.

In the derivation of the admittance of the interface defects $Y_\mr {it}$ , we assumed all traps to be located at the same position in the energy bandgap (single–level approximation). It is possible to extend this model to an ensemble of interface states distributed over a range of energy below the semiconductor conduction band. In this case, each level $j$ contributes with its characteristic admittance $\mr {Y_{it, j}} = {1}/{\mr {R_{it, j}}} + i \omega \;\mr {C_{it, j}}$ , and the total admittance is the integral over all active states. In terms of our equivalent circuit model, we can model the ensemble of trap states as a parallel circuit of many single contribution $\mr {Y_{it, j}}$ , as shown in Fig. 3.1c.

Finally, we need to extract the quantity we are interested in, $Y_\mr {it}$ , from the measurement data. As mentioned in Chapter 2, the result of an impedance measurement is a couple of real numbers that describe the complex impedance of the sample. For MIS structures we use a parallel model, which means that we measure the quantities $\mr {G_m}$ and $\mr {C_m}$ that define the complex admittance $\mr {Y_m} = \mr {G_m} + i \omega \,\mr {C_m}$ . From this data it is easy to correct for the dielectric capacitance, which must be measured accurately and used as a parameter. In this way, we obtain the parallel capacitance and conductance $\mr {G_p}$ and $\mr {C_p}$ , and the equivalent model of the MIS structure is shown in Fig. 3.1d. At this point, we can extract the interface defects admittance from our measurement using the following equations:

$(3.12) \begin{equation} \begin {split} \mr {C_p} &= C_\mr {depl} + \frac {C_\mr {it}}{1 + \omega ^2\tau _\mr {it}^2}\\ \frac {\mr {G_p}}{\omega } &= \frac {C_\mr {it} \omega \tau _\mr {it}}{1 + \omega ^2\tau _\mr {it}^2}.\\ \end {split} \label {gp} \end{equation}$

The first equation is the basis of the Terman method, which is discussed in Section 3.1.2. We already note that this approach requires to calculate the depletion capacitance, for which a theoretical model is needed. Also the doping profile must be known and used as a parameter. In the case of an inhomogeneous doping, the calculation becomes more difficult and numerical methods might be necessary [64]. On the other hand, the conductance depends only on interface defects properties. $\mr {G_p}$ is divided through the angular frequency in order to obtain symmetric peaks as a function of frequency. The method based on the analysis of the conductance is described in Section 3.1.3.

3.1.2 The Terman or high frequency method

The goal of the Terman method is to extract the density of interface traps from the measurement of the CV of the device [65]. This technique relies on a major simplification of the model in Fig. 3.1b, known as the high frequency approximation, which consists of neglecting the admittance $Y_\mr {it}$ . In other words, we assume that the frequency is so high that no trap responds to the AC signal during the sweep. The equivalent model is therefore a series of the dielectric capacitance and that of the depletion region only, whose capacitance $\mr {C_{HF}}$ is given by

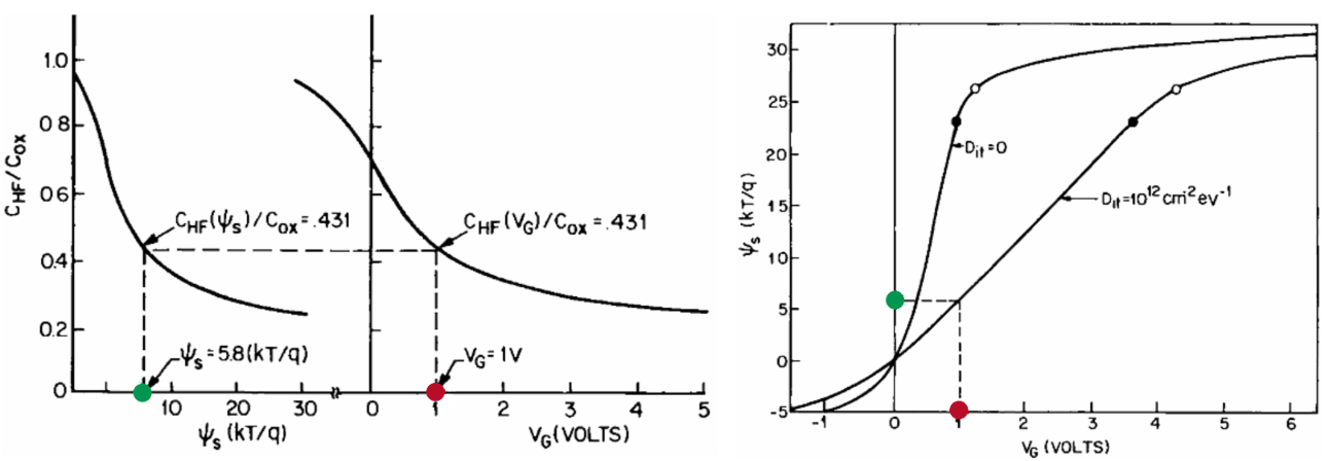
$(3.13) \begin{equation} \mr {C_{HF}}= \left ( \frac {1}{C_\mr {diel}} + \frac {1}{C_\mr {depl}} \right )^{-1}. \label {eqCHF} \end{equation}$

Figure 3.2: The simulated, ideal ( $D_\mr {it} = 0$ ) capacitance as a function of the surface po- tential, in the high frequency approximation (a) and the measured CV curve, $\mr {C_{HF}} (V_\mr {gate})$ (b). These two curves allow us to calculate the real surface potential $\phi _\mr {s} (V_\mr {gate})$ , to be compared with the ideal one (c), from which $D_\mr {it}$ can be extracted (from [38]).

In this case, the information about the interface defects can be indirectly extracted from the behavior of the semiconductor depletion capacitance [38]. In fact, this method is based on the comparison of the measurement with a simulated, ideal curve. The capacitance of the depletion region and that of the interface states are functions of the band bending. It is possible to simulate the ideal curve in absence of trap states, $C_\mr {depl} (\phi _\mr {s})$ , from the device and material properties [38]. Subsequently, from $C_\mr {depl} (\phi _\mr {s})$ we can derive the dependence of $\mr {C_{HF}}$ on $\phi _\mr {s}$ with Eq. (3.13). An example is shown in Fig. 3.2a. The CV measurement provides the experimental curve $\mr {C_{HF}} (V_\mr {gate})$ , as shown in Fig. 3.2b. With such information we can extract the real surface potential as a function of the gate bias, as shown in the example of Fig. 3.2c. We note that the presence of interface states results in a stretch–out with respect to the ideal curve.

The density of interface states, $D_\mr {it}$ , can be calculated from the data in Fig. 3.2. We consider again the charge balance in the MIS structure of Eq. (3.6). The voltage drop at the gate contact is the difference between the applied bias and the band bending of the semiconductor, therefore the total charge can be written as

$(3.14) \begin{equation} Q_\mr {gate}= C_\mr {diel} \left ( V_\mr {gate} - \phi _\mr {s} \right ). \end{equation}$

The charges of the depletion region and that of the interface traps are functions of the surface potential through their respective capacitances:

$(3.15) \begin{equation} Q_\mr {depl}= C_\mr {depl}\; \phi _\mr {s} \quad \quad \mr {and} \quad \quad Q_\mr {it}= C_\mr {it}\; \phi _\mr {s}. \end{equation}$

For a small change of the applied gate bias, we can write

$(3.16) \begin{equation} C_\mr {diel} \; \mr {d}V_\mr {gate} = \left [ C_\mr {diel} + C_\mr {it} \,(\phi _\mr {s}) + C_\mr {depl} \,(\phi _\mr {s}) \right ] \mr {d}\phi _\mr {s} \end{equation}$

from which we derive an expression for the interface trap capacitance:

$(3.17) \begin{equation} C_\mr {it} \,(\phi _\mr {s}) = C_\mr {diel} \left ( \frac {\mr {d}\phi _\mr {s}}{\mr {d}V_\mr {gate}} \right )^{-1} - C_\mr {diel} - C_\mr {depl} (\phi _\mr {s}), \label {termeq} \end{equation}$

where $C_\mr {depl} (\phi _\mr {s})$ is the simulated, ideal curve of Fig. 3.2a, and the derivative $\mr {d}\phi _\mr {s}/\mr {d}V_\mr {gate}$ can be calculated from Fig. 3.2c. This finally allows us to calculate the density of interface states as [38]

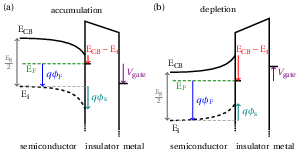
$(3.18) \begin{equation} D_\mr {it} \,(\phi _\mr {s}) = \frac {C_\mr {it}\,(\phi _\mr {s})}{q}. \label {dit} \end{equation}$

In order to determine the energy of the trap states, an additional assumption is necessary. According to the Terman method, only the traps aligned with the semiconductor Fermi level are considered to contribute to the stretch–out of the capacitance curve. This would be possible only if the system under AC excitation reached a quasi–equilibrium situation, for which the position of the Fermi level remains constant and depends only on the value of the DC bias, $V_\mr {gate}$ . In other words, we assume that only the response of a trap located at $E_\mr {CB} - E_\mr {t}$ is in resonance with the small–signal applied to the gate. Such an approximation neglects the contribution of the DC bias to the trapping events at the interface. As we will discuss in the following sections, this can indeed result in an incorrect interpretation of the activation energy of the defects, and to an underestimation of the density of interface states. The energy diagram of this situation is shown in Fig. 3.3 for a n–type semiconductor in accumulation and depletion conditions.

Figure 3.3: Band diagram of a MIS structure in accumulation (a) and depletion condition (b). The trap level at energy $E_\mr {t}$ below the conduction band edge is aligned with the Fermi level.

At each measurement point at a certain $V_\mr {gate}$ corresponds a value of the surface potential $\phi _\mr {s}$ , at which we can calculate the density of interface traps $D_\mr {it}$ with Eq. (3.18) and their location in energy as

$(3.19) \begin{equation} E_\mr {CB} - E_\mr {t} = \frac {E_\mr {g}}{2} - q\phi _\mr {s} -q\phi _\mr {F}, \end{equation}$

where $E_\mr {g}$ is the energy bandgap and $\phi _\mr {F}$ is the Fermi potential, that can be estimated as

$(3.20) \begin{equation} \phi _\mr {F} = \frac {k_\mr {B} \mr {T}}{q} \: \mr {ln} \frac {N_\mr {d}}{n_\mr {i}} \end{equation}$

where $k_\mr {B}$ is the Boltzmann constant, $\mr {T}$ the temperature, $N_\mr {d}$ is the doping profile of the semiconductor and $n_\mr {i}$ its intrinsic carrier density.

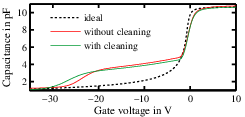
Figure 3.4: (a) Cross–section of the GaN/SiN MIS structure with a silicon doped layer buried in the buffer. (b) High frequency (500 kHz) CV curves of the MIS devices on the two wafers, with and without the AlGaN surface cleaning. The ideal CV curve is also shown.

We apply the Terman method to the devices without the AlGaN barrier introduced in Section 2.1. The gate contact is realized on top of the dielectric layer, while the bulk is connected to the silicon doped layer buried into the GaN buffer, as shown in the cross section in Fig. 3.4a. We use two wafers, one of which has had an additional cleaning (a standard wet chemistry process) at the GaN surface before the deposition of the dielectric. Their high frequency capacitance characteristic are shown in Fig. 3.4b. The shape of the curve in depletion between −30 V and −20 V is due to the non uniform doping profile. In fact, at negative gate bias the depletion region grows in the semiconductor, and the depletion depth is proportional to the doping profile. The steeper part of the CV corresponds to the 10¹⁸/cm³ Si doped layer, the rest to the UID GaN (dopant concentration 10¹⁶/cm³). This fact also explains the discrepancy between the measured curves and the ideal one, simulated using $N_\mr {d} =$ 10¹⁶/cm³. 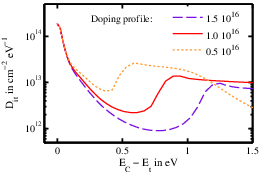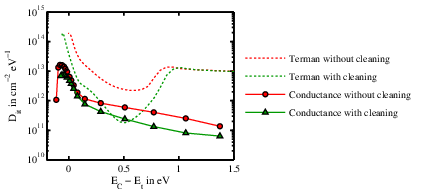We note that the CV of the structures with the additional cleaning is slightly steeper than the other one, which would imply a smaller amount of trapped charge. The results of the Terman analysis are shown in Fig. 3.5. We obtain a “U” shaped distribution close to the conduction band edge, with an average density of 10¹³/(cm² eV). The AlGaN surface cleaning appears to reduce the density of the traps around 0.5 eV of about one order of magnitude.

Figure 3.5: The density of interface traps as a function of the position in energy for the GaN/SiN structures, calculated with the Terman method.

The first limitation of the Terman method is its dependence on parameters, namely the doping profile and the dielectric capacitance. The derivation of Eq. (3.18), which allows us to estimate $D_\mr {it}$ , assumes a uniform doping profile. It has been shown that an incorrect $N_\mr {d}$ value may cause an error of one order of magnitude in determining the density of interface states [66]. From Fig. 3.6a, we can see that also the shape of the $D_\mr {it}$ curve is affected. 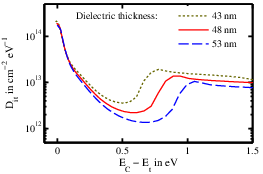The same happens for the dielectric capacitance, for which the exact dielectric thickness has to be estimated or measured. In our case, the measured value of $\mr {t_{diel}}$ is 48 nm, while the nominal value is 50 nm. Discrepancies due to the SiN layer irregularities may result in the underestimation or overestimation of the $D_\mr {it}$ , as shown in Fig. 3.6b for a variation of 5 nm from the correct value.

Figure 3.6: Impact of the parameters used for the $D_\mr {it}$ calculation with the Terman method, on the GaN/SiN sample without cleaning: doping profile (a) and dielectric thickness (b).

A further, more serious limitation is the high frequency approximation. As we explained in the derivation of Eq. (3.18), we assume that the frequency used for the sweep is so high that no traps can follow the AC signal. This allows us to compare the measurement directly with the ideal curve. However, experimental evidence has shown that this interface presents traps with very small time constants, i.e., smaller than 100 ns [47]. It is clear that the high frequency approximation is not valid for these structures. Such a requirement might be met only at frequencies higher than 10 MHz, which would require a dedicated setup with RF probes. Nevertheless, the lower limit for the trapping time constant has not been measured, therefore even higher frequencies might be required.

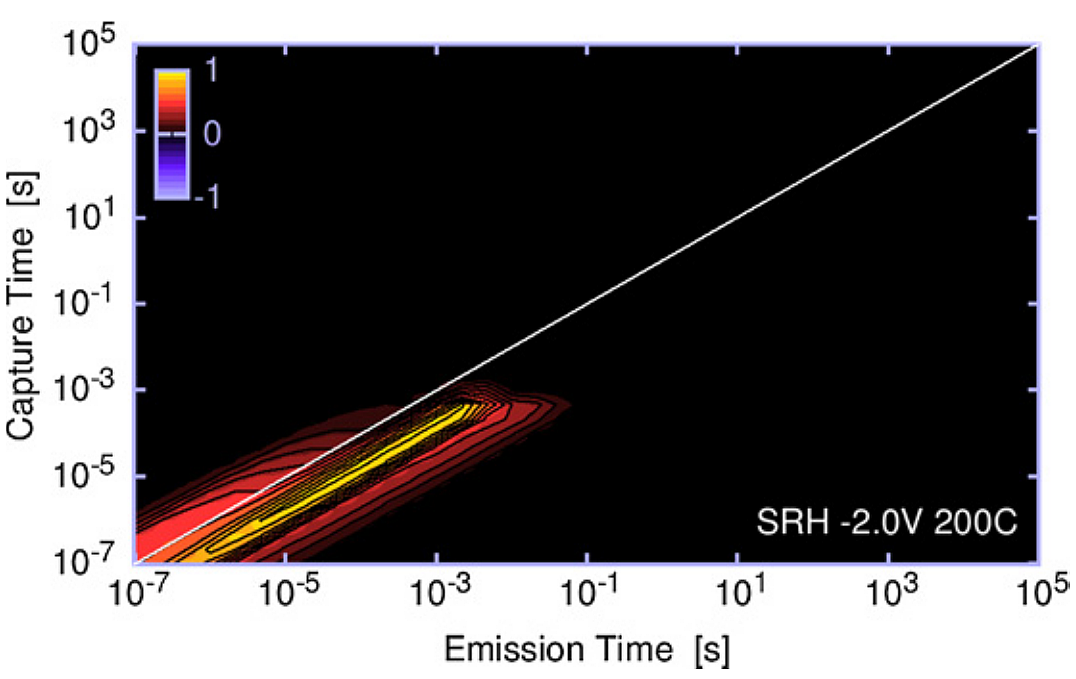
In addition, this method is based on the assumption the Shockley–Read–Hall model through Eq. (3.4), which means that the traps accessible at a certain DC bias are capturing and emitting back all electrons following the AC signal. This would be true if the capture and emission time constants were identical for every defect state, namely $\tau _\mr {c} = \tau _\mr {e}$ . In fact, if we describe this trapping behavior with a capture–emission time (CET) map, in which the amount of device degradation is plotted as a function of $\tau _\mr {c}$ and $\tau _\mr {e}$ , we would obtain a narrow stripe along the diagonal, and zero otherwise [27], as shown in Fig. 3.7a. On the contrary, the CET map for GaN–based devices shows that there are interface states with very different capture and emission time constants [47](see Fig. 3.7b). This means that some traps can capture an electron during the rising part of the AC signal ( $v_0 + \delta \!v$ ), but they cannot emit it when the gate bias reaches again the baseline ( $v_0$ ). For this reason, the assumption of Eq. (3.4) is not adequate for our case.

The last and most important problem of the Terman method is that it cannot be applied to composite GaN/AlGaN structures. As we mentioned in Chapter 1, the presence of the AlGaN layer results in a small–signal behavior that cannot be modelled with the equivalent circuit described in Section 3.1. We will discuss in detail the role of the AlGaN barrier in Section 3.2.1, showing that the model of Fig. 3.1b should be fundamentally modified. It has been shown that the experimental CV curve can be simulated with a high degree of accuracy just by assuming the modified model, without additional interface traps [46]. Since one of the most important assumptions of the Terman method is not met, this method would lead to erroneous conclusions if applied to GaN/AlGaN MIS structures.

Figure 3.7: (a) Simulated capture–emission time map for the Shockley–Read–Hall model (from [27]), and (b) measured CET map for GaN/AlGaN/SiN MIS–HEMTs (from [47]).

3.1.3 The conductance method

In Section 3.1.1 we derived the expression Eq. (3.12) for the parallel conductance, $\mr {G_p}$ , in the case of traps with a single energy $\mr {E_t}$ . It is possible to generalize it for an ensemble of traps distributed in energy, which is a better model of a real system. The integration is possible if we assume the density of traps and the capture probability, which can depend on the surface potential as $N_\mr {it} (\phi _\mr {s})$ and $c_n (\phi _\mr {s})$ , to vary smoothly in a range of few $k_\mr {B}\mr {T}/q$ . This means that we consider $N_\mr {it}$ and $c_n$ constant over a small variation of the surface potential. For this reason, the resolution in energy for $D_\mr {it}$ will be limited. With this assumption we can derive the equation [63]

$(3.21) \begin{equation} \frac {\mr {G_p}}{\omega } = \frac {\mr {C}_\mr {it}}{2\omega \, \tau _\mr {it}} \mr {ln} \left ( 1 + \omega ^2 \, \tau _\mr {it}^2 \right ). \label {gpfit} \end{equation}$

The quantities $\mr {C}_\mr {it}$ and $\tau _\mr {it}$ are extracted with a fit to the experimental curves, and the density of traps is then calculated with Eq. (3.18).

We calculate the parallel conductance from the measured data, $\mr {G_m}$ and $\mr {C_m}$ , with the equation

$(3.22) \begin{equation} \frac {\mr {G_p}}{\omega } = \frac { \omega \, C_\mr {diel}^2 \,\mr {G_m} }{\mr {G_m}^2 + \omega ^2 \left ( C_\mr {diel}+ \mr {C_m} \right )^2 } \label {eqgp} \end{equation}$

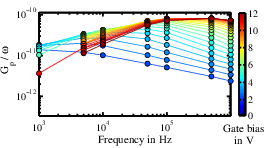
which gives symmetric $\mr {G_p}/\omega$ peaks as a function of frequency, as shown in Fig. 3.8. At every gate bias we obtain a different peak, whose maximum value is proportional to the density of interface states and its resonant frequency is proportional to $\tau _\mr {it}$ .

Figure 3.8: The parallel conductance as a function of frequency of the GaN/SiN structure without the surface cleaning. Each peak is measured at a constant DC bias value; here the data from 0 V to 12 V is shown.

Similarly to the Terman method, we need to associate at each DC bias the energy of the trap which is in resonance with the AC signal, i.e., the one which is aligned with the Fermi level (see Fig. 3.3). The result of the conductance analysis on the GaN/SiN devices is shown in Fig. 3.9. We obtain the same order of magnitude of traps as with the Terman method, but a slightly different shape at energies around 1 eV. The device with the additional cleaning process shows a reduced trap density, although the difference is not as marked as in the previous results. In addition, this technique reveals a drop of $D_\mr {it}$ at energies below −0.1 eV. Negative energies refer to trap states in the dielectric bandgap and above the semiconductor conduction band edge.

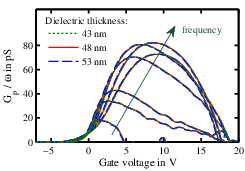
Figure 3.9: Density of interface states of GaN/SiN devices, calculated with the Terman and the conductance method.

Differently from the Terman method, the conductance technique does not depend in the same way on the parameters used. The only parameter in Eq. (3.22) is the dielectric capacitance, which does not have a strong impact on the calculated $\mr {G_p}/\omega$ peaks. In Fig. 3.10 we compare the results by using the measured dielectric thickness and variations of 5 nm, as we did in Fig. 3.6b. The difference in the result is less than the 6%, and this would not affect the $D_\mr {it}$ extraction.

Figure 3.10: The value of the dielectric capacitance used in Eq. (3.22) does not have such a strong effect as for the Terman method. We obtain the same parallel conductance data at 10 kHz (a) and the $\mr {G_p}/\omega$ peaks at all frequencies (b) using varia- tions of the dielectric thickness of 5 nm from the measured value.

However, in conductance measurements we should consider the impact of the series resistance. In fact, we can expect that our impedance measurement model is not fully described by a parallel circuit of $\mr {C_m}$ and $\mr {G_m}$ , but that also a certain resistance $\mr {R_s}$ in series is necessary, especially at high frequency. This accounts for leakage currents through the dielectric, and for the possible resistance arising from the bulk contact through the Si–doped layer. 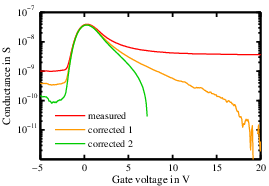This can be seen in the measured $\mr {G_m}$ curves from their behavior at positive bias: the conductance peak over $V_\mr {gate}$ is not symmetric, but a larger value of conductance is reached, as shown in Fig. 3.11a. This is the typical effect of the series resistance [38], and can be corrected with the equations

$(3.23) \begin{equation} \begin {split} \mr {C_{corr}} &= \frac {\mr {C_m} \left ( \mr {G_m}^2 + \omega ^2 \mr {C_m}^2 \right )}{a^2 + \omega ^2 \mr {C_m}^2}\\ \mr {G_{corr}} &= \frac {a \left ( \mr {G_m}^2 + \omega ^2 \mr {C_m}^2 \right )}{a^2 + \omega ^2 \mr {C_m}^2},\\ \mr {with}\quad a &= \mr {G_m} - \left ( \mr {G_m}^2 + \omega ^2 \mr {C_m}^2 \right ) \mr {R_s}\\ \end {split} \end{equation}$

where the series resistance $\mr {R_s}$ is evaluated with the high frequency approximation in accumulation conditions, where the response of the device is assumed to be described by the dielectric capacitance and the series resistance in series. On the contrary, the capacitance curves are not so severely affected. As a result of the correction with the appropriate $\mr {R_s}$ value, the $\mr {G_p}/\omega$ peaks become symmetric. If the wrong series resistance is used, the shape of the curves can be very different. As one can see from Fig. 3.11b, this is true especially at high frequency, where the impact of the series resistance is larger. Such an artifact compromises the calculation of $D_\mr {it}$ , because the fit of the $\mr {G_p}/\omega$ peaks with Eq. (3.21) would not converge in this case.

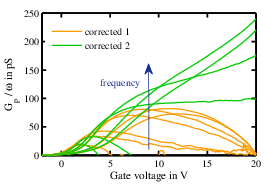
Figure 3.11: The effect of the series resistance parameter in the correction of the parallel conductance data at 10 kHz (a) and of the $\mr {G_p}/\omega$ peaks at all frequencies (b). The first cor- rection (labeled “corrected 1”) is made with the correct parameter, the second (“corrected 2”) with a $\mr {R_s}$ value 15% off the real one.

The conductance method suffers from the same limitation of the Terman method when applied to composite GaN/AlGaN structures. As we pointed out at the beginning of the present chapter, the foundations of this technique lie in the equivalent circuit model of Section 3.1.1. The presence of the AlGaN barrier causes the failure of such an assumption, as we will discuss in Section 3.2.1. For this reason, also this method is not adequate for GaN/AlGaN devices.

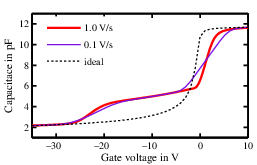
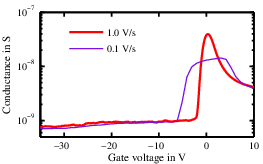
Figure 3.12: CV curves (a) and conductance characteristic (b) at 10 kHz, taken with different measurement speed. The ideal CV curve for the Terman method is also shown.

Finally, a problem common to both methods consists in the dependence of the impedance characteristics on the measurement parameters, which will be discussed in detail in Section 3.2.2. In fact, we find that the CV and conductance curves at the same frequency can vary if the sweep rate is changed. An example is shown in Fig. 3.12. A slow sweep results in a stretch–out of the CV and a broader conductance peak. It is clear that the results from the Terman and the conductance method would be very different using the slow or the fast data. Moreover, such a behavior contradicts the assumption of thermal equilibrium. In other words, the trap states are not in resonance with the AC signal, capturing and emitting electrons following the small–signal oscillations, but the DC bias itself causes a time–dependent right shift of the threshold voltage. As a consequence, we cannot define the “baseline” of the surface potential $\phi _\mr {s,0}$ and assume that the only change in time, $\delta \!\phi _\mr {s}$ , is due to the small–signal variation $\delta \!v$ of the gate voltage. Therefore, the measurements at various speed give very different results because the amount of trapped charge depends on the duration of the transients at each gate bias, which is longer the slower the sweep rate. The failure of this fundamental assumption causes the methods described in this section to give very questionable results even on GaN/SiN MIS structures. We must therefore conclude that the Terman and the conductance method are inappropriate for the characterization of interface traps in GaN–based devices, especially for composite GaN/AlGaN samples.

« Previous Up Next »Contents
Previous: 2.4 Setup for opto-electrical characterization Top: Home Next: 3.2 Impedance characteristics of GaN/AlGaN MIS structures