Impact of Charge Transitions at Atomic Defect Sites on Electronic Device Performance
Chapter 4 Charge Trapping in Field Effect Transistors
4.1 Defects in amorphous silicon dioxide (\(a\)-SiO2)
The content presented in this section has been published in [4, 208, 45].
Both the text and the figures have been adapted from these publications.
4.1.1 SiO\(_2\) structure creation
20 amorphous SiO\(_2\) structures containing 216 atoms were created by simulated melting and subsequent quenching of \(\beta \)-cristobalite as already successfully carried out in previous publications [26]. This specific SiO\(_2\) polymorph was used as its density (2.33 g cm\(^{-3}\)) is closer to a-SiO\(_2\) (2.2 g cm\(^{-3}\)) compared to \(\alpha \)-quartz (2.65 g cm\(^{-3}\)), which is beneficial to obtain a realistic mass density before cell optimizations with density functional theory (DFT). Molecular dynamics (MD) as implemented in the LAMMPS code [192] was deployed using the classical ReaxFF potential [209], calibrated towards Si/SiO\(_2\) systems. This force field was proven in previous publications to be an excellent choice due to its ability to dynamically break and form bonds [34]. The system was heated well up above its melting point to 5000 K and kept at this temperature for full randomization and afterwards cooled down to 0 K at a rate of 6 K ps\(^{-1}\), employing the Verlet algorithm to propagate the system in time using a time step of 0.1 fs. The obtained structures were further relaxed within DFT to reduce internal forces to 0.025 eV/Å. Additionally, the cell parameters were also allowed to change during relaxation to remove any residual mechanical stress in the structures (down to 0.01 GPa). This cell relaxation improves the soundness of the defect calculations compared to previous works where structures were still slightly strained. The computational setup of all presented DFT calculations in this section is given in Appendix E.
4.1.2 Structural analysis
The distributions of the Si–O bond lengths and the O–Si–O and Si–O–Si angles of all 20 generated structures are shown in Fig. 4.1. Bond lengths (\(1.63\textpm 0.02\) Å) and angles (O–Si–O = \(109.47\textpm 4.26\) ° and Si–O–Si = \(143.41\textpm 13.2\) °) are in the same range as previous DFT calculations [15] and are in good agreement with high-energy x-ray and neutron diffraction measurements [210, 12].
The average mass density of the structures is 2.17 g cm\(^{-3}\), which also agrees well with experimental data for SiO\(_2\) thin films on Si (\(2.18-2.27\) g cm\(^{-3}\)) [211]. The following defect calculations were carried out on a single structure characterized by structural parameters consistent with the distribution over all 20 structures. For this structure, all Si atoms are fourfold coordinated with O and all O atoms are twofold coordinated with Si. Its structural parameters are shown as blue bins in Fig. 4.1. In a-SiO\(_2\), characteristic geometrical distances like bond lengths cannot be measured directly by x-ray diffraction, as Bragg’s law cannot be applied in amorphous materials. Nonetheless, the structure factor \(S\) [212], can be extracted by x-ray and neutron diffraction experiments as a function of the scattering vector \(Q\) as described in Section 2.3.2. The comparison of \(S\) of the sample structure to experimental neutron scattering data in \(a\)-SiO\(_2\) [213] is depicted in Fig. 4.2, showing good agreement over the entire \(Q\)-range.
Based on these structural agreements to experiments, we conclude that our final SiO\(_2\) models are a reasonable representation of real a-SiO\(_2\).
4.1.3 Multi-state defect PECs
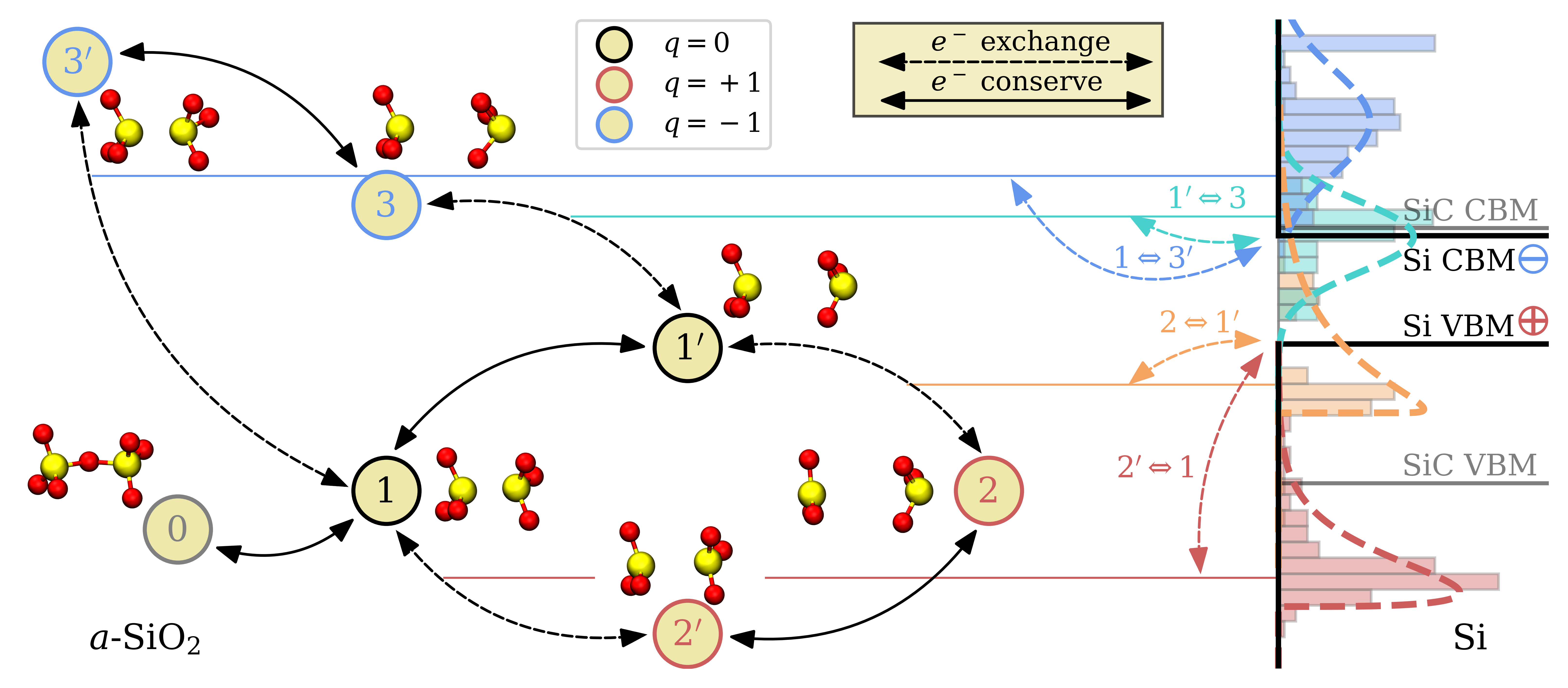
Following the description of multi-state defects in Sections 1.1.1 and 2.1.5, the schematic potential energy curves (PECs) of an oxide defect in three different charge states including metastable configurations is depicted in the context of a Si/SiO\(_2\) band diagram in Fig. 4.3. Hereby, the valence band maximum (VBM) and conduction band minimum (CBM) of the Si substrate act as charge reservoirs as discussed in Section 2.1.4. The PECs can be modeled by calculating the charge transition levels (CTLs), relaxation energies and configuration coordinate changes as discussed in Section 2.1.2. Nonradiative charge transition events are expected to occur over the crossing point (CP) of two energy curves in the classical high temperature limit. The hole trapping mechanism is shown in Fig. 4.3(a) where the defect is initially neutral with a charge transition level \(\varepsilon (0/+1)\) above the Si VBM. By trapping a hole from (or emitting an electron to) the VBM, the defect becomes positively charged, which corresponds to a local energy minimum of the positive PEC \(V^{+}\). Subsequently, the positively charged defect system may relax to a new stable configuration by overcoming a small thermal barrier, depicted as the transition state (TST). This process corresponds to the transitions \(1 \rightarrow 2^\prime \rightarrow 2\) as also illustrated in Fig. 1.1. For the backward transition \(2 \rightarrow 1^\prime \) where the hole is released again from the defect site, the transition is governed by a different classical energy barrier, leading to a different charge transition rate. The same concept can be applied to the electron trapping mechanism as shown in Fig. 4.3(b).
4.1.4 Defect types
In the following, the three analyzed defect types OV, HB and H-\(E^\prime \) are discussed for the three charge states \(q=\) 0, \(+1\), and \(-1\). The defects are shown for these charge states with their electron distribution around the defect site at an isovalue of 0.05 e/Å\(^3\). Initial structures comprising one OV were created by removing a single oxygen within the cell. For the HB, an oxygen atom was replaced by a hydrogen atom. The hydroxyl-E ′ (H-E′ ) center defects were created by placing a hydrogen in the direct vicinity of a bridging O atom at a distance of 1 Å. For all defects, the geometry of the structures was optimized by DFT. First, the positively charged entity of the initial defect configuration was calculated. The resulting structure was subsequently used as a starting point for a geometry optimization in the neutral charge state, followed by a relaxation in the negative charge state. These procedures were repeated for all 144 oxygen sites in the structure to create 144 different initial defect configurations of each defect type in different charge states. For all three kinds, a number of initial defects spontaneously relaxed to puckered configurations [26], where a silicon atom moves through the plane of its three adjacent oxygen atoms, sometimes backbonding to another O atom. These configurations correspond for example to states \(1^\prime \), 2 and 3 of the HB as shown in Fig. 1.1. Additional puckered configurations were created by forcing a relaxed defect structure to a puckered configuration and subsequently relaxing it with our DFT setup.
Oxygen vacancy
An OV for charge states \(q=\) 0, \(-1\) and \(+1\) is shown with its lowest unoccupied molecular orbital (LUMO) (positively charged) or its highest occupied molecular orbital (HOMO) (neutral and negatively charged) localized at the defect site in Fig. 4.4(a-c).
In the neutral state (a), the HOMO is shared between the two silicon atoms to form the so-called dimer configuration, whereas in the positive charge state (b) the electron is localized on a single Si atom and forms a Si dangling bond. This configuration is known as a paramagnetic \(E'\) center and is the most common dangling bond in a-SiO\(_2\) [28, 29]. In addition to the Si–Si bond in the neutral charge state, this electron is shared almost equally within an anti-bonding orbital between the two Si atoms [214]. For the negatively charged OV, the respective HOMO is localized at both adjacent Si atoms. From the numerous possible configurations with a missing oxygen as discussed in [52], only the dimer (or unpuckered) and the puckered configuration, which account for more than 95 % of all relaxed defects, will be analyzed in this work to allow for efficient characterization of the defect parameters. The average Si–Si distances of the relaxed OVs including the standard deviation are shown in Table 4.1.
| Defect: | \(q=0\) [Å] | \(q=+1\) [Å] | \(q=-1\) [Å] |
| OV: | \(2.43 \textpm 0.09\) | \(2.93\textpm 0.21\)/\(4.27\textpm 0.33\) | \(2.60\textpm 0.28\) |
| HB: | \(1.46 \textpm 0.01\) | \(1.59 \textpm 0.08\) | \(1.46 \textpm 0.04\) |
| H-\(E^\prime \): | \(1.61 \textpm 0.01\) | \(1.77 \textpm 0.03\) | \(1.61 \textpm 0.04\) |
For \(q=+1\), two different unpuckered defect configurations were found. First, one of the silicon atoms has a dangling bond (Si–Si distance of \(4.27 \textpm 0.33\) Å, 37 of all relaxed defects) and the second where the electron is shared between two silicon atoms similar to the neutral dimer configuration (Si–Si distance of \(2.93 \textpm 0.21\) Å). Positively charged puckered OVs tend to be lowered in energy when the Si atom finds a fourth O to backbond to. The charge trapping properties of puckered and unpuckered OVs have also been studied across Si/SiO\(_2\) and Si/SiO\(_2\)/HfO\(_2\) interfaces in [215, 216].
Hydrogen bridge
A hydrogen bridge (HB) can form when a hydrogen atom moves into a preexisting oxygen vacancy [49, 217]. A typical HB in three charge states is shown in Fig. 4.5(a-c) with its HOMO in neutral and negative and its LUMO in positive charge state localized at the defect site.
For \(q=0\) and \(q=-1\), the hydrogen atom is bonded to one of the two silicon atoms, whereas for the positive charge state the resulting H is nearly centered between the two Si of the vacancy. The average Si–H bond lengths for the unpuckered configurations are shown in Table 4.1 for all three charge states. Similar to the OV, a positively charged puckered configuration is lowered in energy when backbonded to a fourth O atom.
Hydroxyl-E\(^\prime \) center
A H-E′ center forms, when a hydrogen atom becomes attached to an O while breaking an elongated Si–O bond [34] and thereby forms a hydroxyl group. The H atom is then bound to an O atom with an adjacent dangling bond at a threefold-coordinated Si atom. An example of a typical H-\(E^\prime \) is shown in Fig. 4.6 in the neutral (a) and positive charge state (b).
Most of the 144 initial configurations with a hydrogen close to a bridging oxygen relaxed into a H-\(E^\prime \) center in the neutral charge state, while 5% reconfigured into a geometrically similar but metastable defect, the so-called [SiO\(_4\)/H]\(^0\) centers [34]. Both Si–O bonds are still intact for these unstable configurations but highly strained to \(\geq \) 1.7 Å. For \(q=+1\), the oxygen remains attached to both silicon atoms. The mean and the standard deviation of the Si–O bond lengths of the unpuckered H-\(E^\prime \) are shown in Table 4.1 for all three charge states.
Negative charge state: Several different configurations were found for the H-E′ center in the negative charge state with four of them shown in Fig. 4.6(c-f). The most stable configuration consists of an intact Si–O bond with the H getting attached to a nearby Si atom making it fivefold coordinated (f) [218, 217]. This configuration is on average 1.5 eV lower in total energy compared to configurations where the Si–O is broken similar to the neutral and positive charge state (c-d) or the oxygen vacancy like configuration (e). Occasionally, these states can also have puckered configurations, which are generally even higher in energy as shown in Section 4.1.6 and will therefore be omitted. Energy barriers for transitions to the stable configuration were calculated with CI-NEB and are presented in Fig. 4.7.
Depending on the configuration, the defect relaxes into the minimum energy configuration with almost no barrier (\(<0.05\) eV) with the H moving to the Si opposite the hydroxyl group while the barrier for an attachment of H to the adjacent Si is rather large (\(>1.8\) eV) for the calculated site. After trapping an electron (similar to \(1 \rightarrow 3^\prime \) in Fig. 1.1), the defect is expected to briefly stay in one of these configurations before the O is bound to the Si atoms again and H gets attached to one of the Si (\(3^\prime \rightarrow 3\)). Due to the small transition barriers and comparably high total energies, the configurations (c-e) are considered to be local minima of the PEC and thus metastable. The minimum configuration will be referred to as H-\(E^\prime \) \(_{\mathrm {min}}^{-}\) in the following. Upon the release of an electron, the hydrogen was often found to become interstitial and consecutively creates a defect, potentially at a different position in the oxide (\(3 \rightarrow 0\) vs. \(3 \rightarrow 1\)).
4.1.5 Formation energy
The formation energies \(E_{\mathrm {form}}\) of the neutral defects are shown in Fig. 4.8. For all defect types, the extracted parameters of the distributions are given in the plot. Formation energies for oxygen vacancies are given with respect to the pristine bulk system. This reference makes the total values arbitrary as in reality OVs are mostly introduced in SiO\(_2\) during oxidization, but occasionally can also be created in the vicinity of already existing OVs during an applied bias [219]. Furthermore, we approximate the chemical potentials used in Eq. (2.11) with the total energies obtained with our DFT setup, half the energy of an H\(_2\) molecule for \(\mu _\mathrm {H}\) and half the energy of an O\(_2\) molecule for \(\mu _\mathrm {O}\). As can be seen in Fig. 4.8 (top), puckered OV configurations have a significantly higher formation energy than the unpuckered configurations. The accumulated formation energies of the OV defects can both be described by a normal distribution, the fitting parameters are shown in the figure.
For the HB defects, the formation energies are given with respect to their precursor configuration (unpuckered and puckered OVs respectively) in Fig. 4.8(b), which is assumed to be the oxygen vacancy at the respective defect site. Furthermore, in Fig. 4.8(c), \(E_{\mathrm {form}}\) of HB defects is also given with respect to the perfect bulk system to compare the formation energies of the two hydrogen related defect types. Since in the case of the unpuckered HB the distribution of the formation energies is asymmetrically shifted to higher values, as can be seen in Fig. 4.8(b), a Weibull distribution was chosen here for the most suitable fit which is given by equation C.1 shown in the appendix. Puckered HB configurations tend to posses lower \(E_{\mathrm {form}}\).
For the majority of the HB defects (61.5 %), the formation energy is negative when referencing to an already existing OV, indicating that the HB is actually the preferred defect configuration in this case. Nevertheless, due to the extremely high formation energy of the HB in a perfect bulk system, the creation of HBs is limited by the already low concentration of oxygen vacancies (\(10^{14}-10^{18}\) cm\(^{-3}\)) in a-SiO\(_2\) thin films [16, 220, 221].
The formation energies of the last investigated defect, the H-\(E^\prime \), are again given with respect to the bulk system. Compared to the two other defect types, \(E_\mathrm {form}\) gives feasible concentrations for H-\(E^\prime \) defects only limited by the number of hydrogen atoms in the oxide (\(10^{20}-10^{22}\) cm\(^{-3}\)) [222, 223]. Defects with formation energies \(>4.5\) eV were all identified as [SiO4/H]0 defects. These configurations are metastable with a similar energy compared to H being interstitial and with only a small barrier to relax to a H-\(E^\prime \) as shown in [34]. Because they are unlikely to form naturally compared to the H-\(E^\prime \) centers, they are excluded from the normal distribution fit and will not be analyzed in the further discussions.
4.1.6 Transitions without charge transfer
In this section, the metastable defect configurations, which correspond to the states denoted with a prime in Fig. 1.1 and the local minima in Fig. 4.3, are analyzed in terms of their relative energy and activation barriers with respect to the stable configuration.
Metastable configurations
As described in Section 4.1.4, the three investigated defect types can also all exist in puckered configurations in all charge states. Some of the puckered defects formed spontaneously during relaxation, while the remaining initial puckered configurations were intentionally perturbed by moving the central Si atom through its plane of the backbonded O atoms in order to deliberately create such a state. The energy differences between puckered and unpuckered configurations in the respective neutral, negative and positive charge states are shown in Fig. 4.9.
Normal distributions were fitted to the energy differences with the parameters given in the plot. The unpuckered OV is clearly the preferred configuration with substantially lower energies. For the hydrogen related defects, HB and H-\(E^\prime \), both the puckered and the unpuckered can be the configuration lower in energy, depending on the respective atomic surroundings of a certain defect. The transition barriers between these two configurations are discussed in the following.
Transition barriers
Transition barriers between puckered and unpuckered configurations for all three defect types in the negative charge state were calculated using the CI-NEB method as described in Section 2.1.5. Barriers for positively charged and neutral defects have been already reported in [26]. Due to the enormous amount of core hours needed for such calculations (> 10\(^4\) h), only a small number (< 10) of barriers for each transition could be carried out. The results are shown in Fig. 4.10. For negatively charged OV and HB defects, these barriers correspond to the \(3 \leftrightarrow 3^\prime \) transition. For the H-\(E^\prime \), these calculations are a bit artificial as the unpuckered configurations (Fig. 4.6(c-e)) are already highly unstable and rapidly relax into the H-\(E^\prime \) \(_{\mathrm {min}}^{-}\) configuration as shown in Section 4.1.4. In Fig. 4.10(a), three different energy profiles are plotted as a function of the configuration coordinate to show the variety of the possible transitions. The energy barriers for the transition from the stable to the metastable state are shown in Fig. 4.10(b). Barriers vary from 1.5 to 2.5 eV (OV), 0.8 to 2.7 eV (HB) and 0.95 to 2.9 eV (H-\(E^\prime \)). The broad range of activation energies for these thermal transitions can be directly linked to the different timescales of defects staying electrically inactive (ps to years [1]).
4.1.7 Charge transition level
As described in Section 2.1.3, the CTL corresponds to the Fermi level \(E_{\mathrm {F}}\) at which the formation energies of a defect in two different charge states are equal. In other words, the thermodynamically preferred charge state of the defect depends on the relative position of its trap level to the Fermi level. When a defect traps a charge, the localization of the electron in the oxide disturbs the electrostatics of the device, which alters important device properties like the threshold voltage [2, 46]. The CTL is the only defect parameter which is directly accessible through electrical experiments. By applying a gate bias to a MOS device, the position of the trap level can be shifted due to band bending near the interface and the occurring electric field in the oxide as described in Section 2.1.4. When the Fermi level matches the CTL, both involved charge states are equally stable resulting in equal occupancy and maximum power of the RTN signal [224]. In principle, the CTL of a defect is an inherent property of the host material, e.g. the oxide of a MOSFET, independent of the electronic bands of a potential substrate. With that being said, the morphology of the interface to the substrate can influence the CTL indirectly via strain or changes in the stoichiometry. Furthermore, the interfacial environment could give rise to entirely new defects not present in the bulk oxide. However, an in-depth treatment of these effects is beyond the scope of the present work and should be investigated separately in the future.
Literature values of the VBM band offset of SiO\(_2\) and Si from spectroscopy experiments are in the range of 4.3 to 4.7 eV [225, 226, 227], depending on the measurement techniques used and the sample growth conditions. In the following,the Si/SiO\(_2\) VBM band offset is set to 4.5 eV for all calculations involving the electronic structure. The crystalline silicon (c-Si) band gap was calculated using our standard DFT setup and is slightly overestimated to 1.38 eV while the SiO\(_2\) band gap was underestimated to 8.1 eV compared to the well-known values (1.1 eV for Si and 8.9 eV for SiO\(_2\)). The discrepancy to measured band gaps of Si crystals and SiO\(_2\) oxides is caused by the employment of the PBE0_TC_LRC hybrid functional for our calculations, which tends to systematically overestimate band gaps of semiconductors and underestimate band gaps of insulators [228]. For the SiC/SiO\(_2\) system, experimental and DFT values for the VBM band offset range from 2.2 to 2.9 eV above the SiO\(_2\) VBM [229, 230, 231], depending on the processing and annealing condition and the orientation of the interface. Based on these various literature values, we set the VBM offset to 2.7 eV with a band gap of 3.3 eV for 4H-SiC [231] in the following.
CTLs were calculated for all possible transitions depicted in Fig. 4.3. Following the commonly employed band edge approximation as described in Section 2.1.4, interactions of defects are limited to the band edges of the Si substrate, which is illustrated with arrows in the shown state diagrams. Note that the uncertainties of band alignments and energy values obtained from DFT calculations have to be considered when analyzing CTLs in the context of a band diagram. Only defects where the electron is fully localized at the defect site for both charge states are considered for the calculations. Not all defects converged into both stable puckered and unpuckered configurations in every charge state, limiting the possible charge transitions, e.g. the hole trapping mechanism from a 4-state defect \(1 \leftrightarrow 1^\prime \leftrightarrow 2 \leftrightarrow 2^\prime \leftrightarrow 1\) to a 3-state \(1^\prime \leftrightarrow 1 \leftrightarrow 2^\prime \) or a 2-state \(1 \leftrightarrow 2^\prime \) defect. This is for instance the case when the Si of a positively charged H-\(E^\prime \) defect has no fourth O in its atomic environment to backbond to, meaning that no stable puckered configuration (2) exists at this defect site. The actual number of \(n\)-state defects can not be sufficiently determined via this approach, as it is quite difficult to verify if a certain configuration really does not exist or if the defect system only relaxed to a different local minimum during the DFT geometry optimizations due to an inadequate starting point. Hence, all possible CTLs are shown in a normalized histogram for all calculated transitions in the following, regardless the number of stable states of a certain defect. The correlations of trap levels of 4-state defects will be further analyzed in Section 4.1.9. The CTL data is plotted in the context of a Si/SiO\(_2\) and a Si/SiC band diagram with the corresponding atomic configurations for a respective charge transition shown on the left side for each defect type.
Oxygen vacancy
The CTLs of oxygen vacancies for both charge transitions and all three defect configurations are shown in Fig. 4.11.
Although OVs are typically introduced in the system during oxidization, a precursor configuration (0) is shown in the figure, as it has been suggested that an OV can also be generated near an already existing OV or near a wide O–Si–O angle when two electrons are trapped at these sites [219]. The majority of the \(1\leftrightarrow 2^\prime \) transitions lie far below the Si valence band maximum while the \(1^\prime \leftrightarrow 2\) transitions have substantially higher CTLs. OVs can therefore capture a hole mostly via the \(1^\prime \leftrightarrow 2\) transition, which requires the positively charged OV to be in the puckered configuration corresponding to the \(E^\prime _\gamma \) center [52]. When the defect relaxes to the \(2^\prime \) state, the subsequent CTL \(1\leftrightarrow 2^\prime \) lies energetically too low to exchange charge carriers with the VBM of Si. This process could explain disappearing defects or anomalous random telegraph noise (RTN) as reported in [133]. Furthermore, the low CTLs of OVs could give an explanation for BTI also reported in Si/SiC devices [46]. The \(1 \leftrightarrow 2^\prime \) and \(1^\prime \leftrightarrow 2\) transitions of the OV are asymmetrically distributed due to the two configurations of the positively charged OV (see Section 4.1.4) and were therefore fitted with a Weibull distribution (Eq. C.1) with the fitting parameters given in Table 4.2.
| Normal Distribution | ||||
| Defect | Transition | \(\mu \) [eV] | \(\sigma \) [eV] | |
| OV | \(1\leftrightarrow 3^\prime \) | 7.38 | 0.67 | |
| \(1^\prime \leftrightarrow 3\) | 5.89 | 0.46 | ||
| HB | \(1\leftrightarrow 2^\prime \) | 4.35 | 0.50 | |
| \(1\leftrightarrow 3^\prime \) | 5.72 | 0.45 | ||
| \(1^\prime \leftrightarrow 3\) | 5.94 | 0.66 | ||
| H-\(E^\prime \) | \(1\leftrightarrow 2^\prime \) | 5.08 | 0.52 | |
| \(1^\prime \leftrightarrow 2\) | 4.94 | 0.50 | ||
| \(1\leftrightarrow 3^\prime \) | 5.70 | 0.29 | ||
| \(1\leftrightarrow 3\) | 4.24 | 0.42 | ||
| Weibull Distribution | ||||
| Defect | Transition | Loc c [eV] | Shape b [eV] | Scale a |
| OV | \(1\leftrightarrow 2^\prime \) | 1.10 | 1.26 | 0.63 |
| \(1^\prime \leftrightarrow 2\) | 3.61 | 0.87 | 1.05 | |
| HB | \(1^\prime \leftrightarrow 2\) | 3.60 | 1.10 | 1.05 |
This asymmetry is due to sporadically occurring OV configurations in the positive charge state that relatively lower the total energy of the defect system, namely puckered OVs with a backbonded Si atom as already discussed in Section 4.4. Hence, it is confirmed that in a MOSFET during normal operation, it is unlikely for an OV to exchange charge carriers with the Si substrate in ultra-scaled devices [26, 30, 217, 31]. Still, the \(\varepsilon (0/+1)\) CTLs of OVs are in a reasonable energy range to trap holes from the VBM of a SiC substrate. For the \(0/-1\) transitions on the other hand, a portion of the \(1^\prime \leftrightarrow 3\) and the \(1\leftrightarrow 3^\prime \) CTLs are in the vicinity of the Si and SiC CBM and thus OVs have to be considered as a possible cause for electron capture events during operation. The total effect of OV on BTI is limited by the low number of oxygen vacancies in \(a\)-SiO\(_2\) as discussed in Section 4.1.5. It should be noted that the OV is also stable in charge state (\(+2\)), which might be of interest for future investigations concerning the hole trapping behavior in SiO\(_2\)/SiC systems.
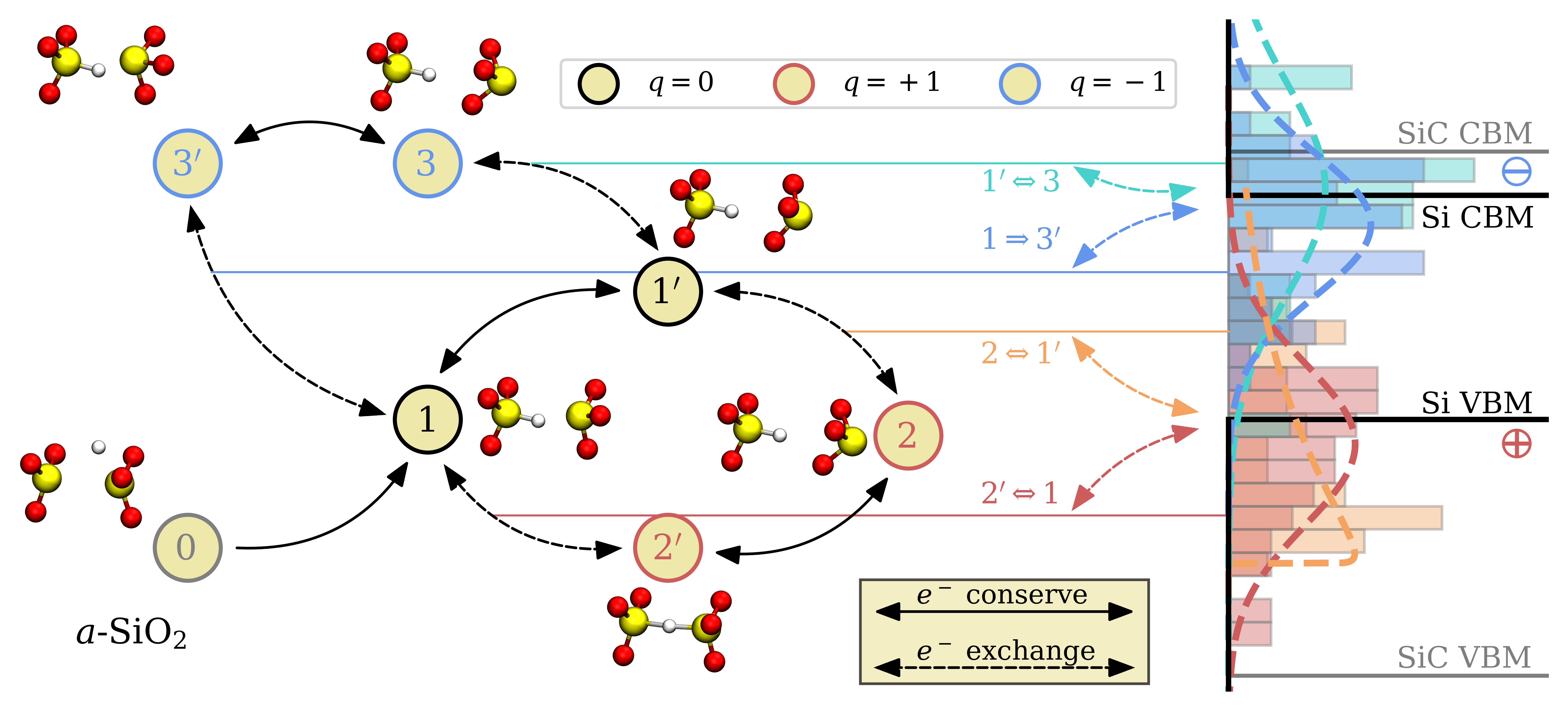
Hydrogen bridge
For the two defect types involving H the situation is completely different. The charge transition levels are shown in Fig. 4.12 with their corresponding atomic configurations on the left side.
The asymmetric distribution of the \(2 \leftrightarrow 1^\prime \) CTLs can be explained by backbonded puckered HB defects in the positive charge state occurring at certain sites in the structure (see Section 4.1.4). Similar to the OV defects, these backbonded HBs are lower in energy compared to defects where no fourth O for backbonding is nearby in the structure. Fitting parameters for normal and Weibull distributions for all transitions are again given in Table 4.2. In contrast to the OV, the majority of the HB defects possess trap levels close to the band edges of the Si substrate, which would make them promising defect candidates to explain reliability degrading phenomena induced by electron as well as hole trapping. Nevertheless, as discussed in Sec. 4.1.5, the concentration of HBs is strongly limited by the number of OVs in the oxide. The high formation energies of HBs in a vacancy free bulk system limit their concentration and thus the influence of this defect type on reliability phenomena is likely negligible.
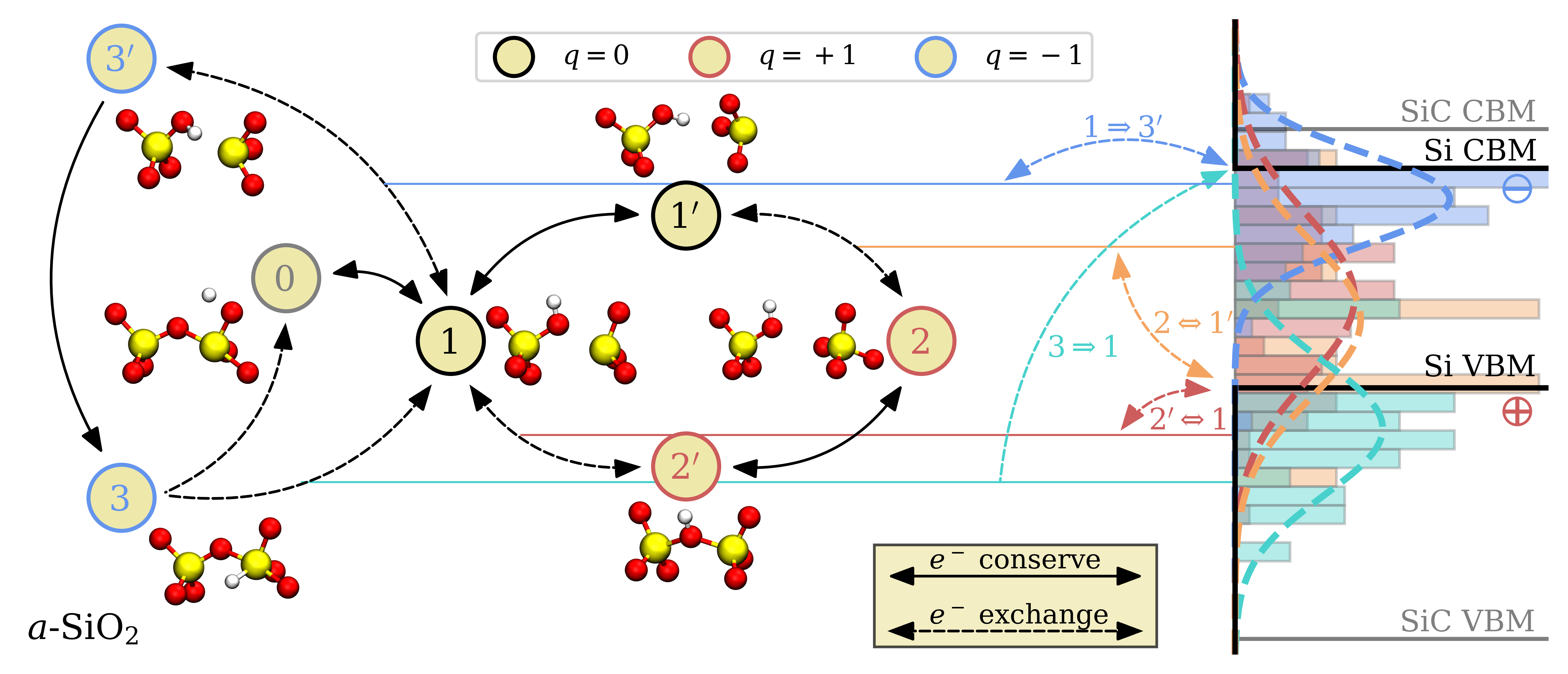
Hydroxyl-E\(^\prime \) center
The state diagram of H-\(E^\prime \) defects with their according CTLs are shown in Fig. 4.13.
Both \(\varepsilon (0/+1)\) CTLs of H-\(E^\prime \) are distributed across the VBM of Si which makes them reasonable defect candidates for trapping holes from the substrate. CTLs for all transitions were fitted with a normal distribution with the fitting parameters given in Table 4.2. The \(1\leftrightarrow 3^\prime \) CTLs near the conduction band edge correspond to the negatively charged metastable H-\(E^\prime \) configurations shown in Fig. 4.6. Additionally, the \(1\leftrightarrow 3\) CTLs near the VBM of silicon correspond to defects with the H-\(E^\prime \) \(_{\mathrm {min}}^{-}\) configuration in the negative charge state. As all other negatively charged H-\(E^\prime \) configurations, puckered or unpuckered, rapidly relax into this minimum configuration as shown in Fig. 4.7, we argue that mainly CTLs corresponding to the negatively charged minimum configuration are detectable in real oxides. Note that the neutral level in this transition can also correspond to the \(1^\prime \) state, depending on the atomic environment. Compared to the hole trapping mechanism, the \(3\rightarrow 1\) CTLs of the H-\(E^\prime \) are energetically farther away from the respective charge reservoir, which reduces the total amount of charge trapping defects in the oxide, thus providing a sensible explanation for the suppressed electron trapping behavior observed in Si/SiO\(_2\) MOS devices.
4.1.8 Non-radiative multi-phonon transitions
In this section, the PECs of H-\(E^\prime \) defects in the harmonic approximation are constructed by fitting parabolas to the equilibrium and relaxation energies of the defects in different charge states. The classical energy barriers for all single charge capture and emission processes are subsequently extracted from the CPs of the PECs. Furthermore, it is shown that the \(-1/0\) (\(+1/0\)) transition is energetically always favorable compared to the \(-1/+1\) (\(+1/-1\)) transition.
Relaxation energies
As discussed in Section 2.1.3, relaxation energies give information about the shape of potential energy surfaces in different defect charge states, in particular the curvature near the energy minimum, as illustrated in Fig. 2.4. Within the harmonic approximation, the CP and hence the classical barrier between two differently charged PEC of a defect is completely determined by the relaxation energies and the trap level as also outlined in Appendix B. Therefore, \(E_\mathrm {Relax}\) heavily influences the resulting capture and emission time constants of the defect [1]. Relaxation energies for charge transitions at the oxide defects were calculated according to Eq. 2.13. When the charge state changes from 0 to \(-1\) (\(+1\)), the relaxation energy will be denoted in the following as \(E\mathrm {_{Relax}^{0/-1}}\) (\(E\mathrm {_{Relax}^{0/+1}}\)) and vice versa \(E\mathrm {_{Relax}^{-1/0}}\) (\(E\mathrm {_{Relax}^{+1/0}}\)). \(E\mathrm {_{Relax}}\) can also be interpreted as the amount of energy being transferred from the defect to the thermal bath after a radiative charge transfer. The distributions of relaxation energies for each defect type are presented in Table 4.3.
| Relaxation Energies | |||
| Defect Type | Transition | Mean [eV] | Std. Dev. [eV] |
| OV | \(0/-1\) | 1.18 | 0.34 |
| \(0/+1\) | 1.5/2.53 | 0.17/0.36 | |
| \(-1/0\) | 1.78 | 0.25 | |
| \(+1/0\) | 2.25/3.5 | 0.18/0.42 | |
| HB | \(0/-1\) | 1.72 | 0.42 |
| \(0/+1\) | 2.20 | 0.17/0.29 | |
| \(-1/0\) | 1.76 | 0.41 | |
| \(+1/0\) | 2.21 | 0.36 | |
| H-\(E^\prime \) | \(0/-1\) | 1.97 | 0.28 |
| \(0/+1\) | 2.98 | 0.32 | |
| \(-1/0\) | 1.59 | 0.1 | |
| \(+1/0\) | 2.4 | 0.45 | |
| \(+1/-1\) | 13.14 | 0.21 | |
| \(-1/+1\) | 7.87 | 0.9 | |
A small number of single point calculations did not meet the convergence criteria for some charged defects, as these calculations are performed on unrelaxed structures. Most of the relaxation energies for all defect types and possible charge transitions are distributed between 1 and 4 eV. The relaxation energies for charge transitions from or to the negative charge state tend to be lower in energy for most of the defects, with the majority (\(\approx 75\) %) below 2 eV (100 % for \(E\mathrm {_{Relax}^{0/-1}}\) of the OV). For the \(+1/0\) and \(0/+1\) transition of the OV and HB two peaks are visible. This is due to the two different OV configurations in the positive charge state as described in Section 4.1.4. Relaxation energies between negatively and positively charged defect states are significantly higher compared to the neutral/charged transitions which has a crucial impact on the charge transition barriers as will be shown in the following.
Potential energy curves
Parabolas were fitted to minimum and relaxation energies of H-\(E^\prime \) defects to extract the classical transition barriers from the CP of two PEC for charge exchange with a Si substrate as discussed in Section 2.1.4. An example for the fitted PECs of an H-\(E^\prime \) defect is shown in Fig. 4.14(a-c), where the parabolas of different charge states are shifted as a function of the Fermi level. This is because the the positions of the parabolas are determined by the CTL, which directly depends on the Fermi level according to Eq. 2.11. Since the CP is not dependent on the value of the configuration coordinate change \(\Delta Q\) (see also Appendix B), \(\Delta Q =1\) can conveniently be set for the extraction of all energy barriers. PECs are fitted for Fermi levels at the \(\varepsilon (0/+1)\) and \(\varepsilon (0/-1)\) CTLs (a and c) and for a Fermi level inside the band gap of Si (b).
Charge transition barriers of hydroxyl-E\(^\prime \) centers
The classical energy barriers extracted from the fitted PECs for 78 different H-\(E^\prime \) defects are shown in Fig. 4.15(a-f) for Fermi levels at the VBM (4.5 eV), inside the band gap (5.1 eV) and at the CBM of the Si substrate (5.8 eV). Hereby, the Si band gap was calculated with the same DFT setup as for the calculations in \(a\)-SiO\(_2\).
For the \(-1/0\), \(0/+1\) and \(-1/+1\) transitions, the energy barriers become higher with increasing Fermi level while the opposite is true for \(0/-1\), \(+1/0\) and \(+1/-1\) transitions. This behavior can directly be linked shift of the CP of the parabolas as illustrated in Fig. 4.14. However, processes involving three particles have a much smaller effective cross section, as the probability of three particles to collide becomes vanishingly low. Additionally, the barrier for a 0/\(q\) charge transition is lower than for a transition involving two charge carriers for all investigated Fermi levels as shown in Fig. 4.16(a,b), making them also energetically more favorable.
Hence, it was shown that the transitions \(3 \rightarrow 2^\prime \) and \(2 \leftrightarrow 3^\prime \) are unlikely, although not completely impossible, to occur compared to processes where only one electron or holes is exchanged.
4.1.9 Defect correlations
In this section, correlations of certain defect properties are analyzed. It will be demonstrated how different CTLs (e.g. \(1^\prime \leftrightarrow 2\) and \(1 \leftrightarrow 2^\prime \)) of the same defect are related to each other. Furthermore, the dependence of CTLs on formation energies and the atomic environment of the defects is shown.
CTLs of puckered and unpuckered defects
The different CTLs of single defects are correlated for hole traps in Fig. 4.17(a) and for electron traps in Fig. 4.17(b).
In this plot, each data point corresponds to one defect, the relevant band edges of the Si bulk for charge exchange are drawn as red (VBM) and blue (CBM) lines, respectively. Only defects where all four configurations of Fig. 4.3 converged for the respective charge trapping mechanism are used for this analysis. For the OV, defects with the \(1^\prime \leftrightarrow 2\) CTL near the VBM of the Si substrate have very deep \(1 \leftrightarrow 2^\prime \) levels when referenced to the Si VBM. These deep levels can explain defects staying electrically inactive over a long time (months) after being charged according to the \(1^\prime \leftrightarrow 2\) transition. This effect can also be observed for the HB and H-\(E^\prime \) defects, but is weakened for this process due to the vicinity of the CTLs to the band edges and the more linear correlation of the transition levels. For all three defect types, the \(1 \leftrightarrow 3^\prime \) levels have no clear dependency on the \(1^\prime \leftrightarrow 3\) levels, but the CTLs of a single defect can also differ by more than 1 eV.
CTLs and structural properties
In Figs. 4.11 – 4.13, the calculated CTLs are shown regardless of the probability that a certain defect will actually form. To analyze the plausibility of the occurrence of a certain CTL, a correlation plot of the formation energies and the \(1 \leftrightarrow 2^\prime \) and \(1 \leftrightarrow 3^\prime \) CTLs of the unpuckered defects is presented in Fig. 4.18.
The color gradient illustrates a characteristic geometrical quantity of the neutral precursor configuration for each defect type: For OVs the distance of two silicon atoms before the oxygen atom between them was removed (Fig. 4.18(a,d)), for the HB the distance between two silicon atoms of an OV before the hydrogen was captured (Fig. 4.18(b,e)) and for the H-\(E^\prime \) the length of the two Si–O bonds before the bond was broken by a hydrogen getting attached to the O (Fig. 4.18(c,f)).
Oxygen vacancies which have their CTL closer to the band edges of the silicon substrate have comparably higher formation energies, which emphasizes the low probability of electrically active OVs. Hydrogen bridges preferably form at prolonged Si–Si distances of an OV, as is indicated by the color gradient at lower formation energies. The \(\varepsilon (0/+1)\) transition with the lowest formation energies are below the silicon VBM, while defects with \(\varepsilon (+1/0)\) CTLs in the middle of the band gap are less likely to form. Transitions at HB show a similar characteristic, where defects with the lowest \(E_{\mathrm {form}}\) have \(\varepsilon (0/-1)\) CTLs close to the CBM of the substrate while for higher formation energies the \(\varepsilon (0/-1)\) CTLs tend to be located within the Si band gap. It is also confirmed from this analysis that H-\(E^\prime \) defects form preferably at strained Si–O bonds [33]. These are also the defects which have the highest chance to capture a hole from the Si substrate, as their \(\varepsilon (0/+1)\) CTLs are close to the Si VBM. The H-\(E^\prime \) \(0/-1\) transitions show only weak dependency on the formation energy for both \(1\leftrightarrow 3^\prime \) and \(1 \leftrightarrow 3\) (denoted as configurations involving the H-\(E^\prime \) \(_{\mathrm {min}}^{-}\) configuration) and their CTLs are mostly independent of the corresponding \(E_{\mathrm {form}}\) and the Si–O bond lengths.
4.1.10 Discussion
Three major defect types in amorphous SiO\(_2\) were investigated, namely the oxygen vacancy (OV), the hydrogen bridge (HB) and the hydroxyl-\(E^\prime \) center (H-\(E^\prime \)), providing a large data set of their defect properties. By calculating the formation energies \(E_\mathrm {Form}\), the charge transition levels (CTLs), the relaxation energies \(E_\mathrm {Relax}\) and the meta-stability of the defects, a multi-state defect model was developed to describe both electron and hole capture in a unified manner. To account for the amorphous nature of SiO\(_2\) thin films, a large ensemble of structural and electronic parameters of the aforementioned defects was calculated in different charge states on a statistical level.
Analogous to the already well investigated neutral and positively charged defects, stable and metastable configurations of negatively charged defect were found. The negatively charged defect configuration where a H attaches to a Si making it fivefold coordinated was named H-\(E^\prime \) \(_{\mathrm {min}}^{-}\), as all other discovered negatively charged H-\(E^\prime \) proved to be metastable with almost vanishing energy barriers to relax to H-\(E^\prime \) \(_{\mathrm {min}}^{-}\). Furthermore, energy barriers between puckered and unpuckered configurations in the negative and neutral charge state of all defect types were calculated with the climbing image nudged elastic band method (CI-NEB) and range from 0.8 to 3 eV. The metastable states and their according transitions to the stable configuration in the same charge state can explain the enormous range of time scales of point defects staying electrically inactive.
It was shown for all three defect types that both \(E_\mathrm {form}\) and CTLs for electron and hole capture are well represented by either a normal or a Weibull distribution. Thereby it is confirmed that the majority of the CTLs of OVs for hole capture processes are energetically too low with respect to the VBM of a Si substrate to interact with its charge carriers. Puckered OVs have CTLs distributed around 1 eV below the Si VBM. When a puckered OV traps a hole (\(1^\prime \leftrightarrow 2\)) and relaxes to an unpuckered configuration (\(2 \leftrightarrow 2^\prime \)), the according \(2^\prime \leftrightarrow 1\) CTL is energetically too low to exchange charge carriers with the VBM. This procedure may explain vanishing defects in irradiated oxides, where toggling signals caused by \(E^\prime \) centers can be detected before the signals disappear as reported in [232].
Furthermore, it was shown that OVs have CTLs for hole trapping near the VBM of SiC substrates and could therefore be a cause for BTI observed in SiC/SiO\(_2\) devices. Also, for the \(0/-1\) transition, OV defects can occasionally have CTLs which are close to the Si conduction band minimum (\(1 \leftrightarrow 3^\prime \)) or inside the band gap of the Si substrate (\(1^\prime \leftrightarrow 3\)), which would make them suitable defect candidates to capture electrons. Nevertheless, as a consequence of the small number of OVs in SiO\(_2\), which is essentially determined by the highest oxidation temperature [233, 234] due to its high formation energy in the SiO\(_2\) bulk (5.6\(\textpm \)0.5 eV), the total influence of OVs on charge trapping processes is reduced compared to H related defects. Hence, OVs with \(\varepsilon (0/-1)\) CTLs near the CBM of the substrate tend to have comparably low concentrations and can thus be neglected for electron capture processes. Therefore, it is concluded that OVs only play a minor role concerning the electron capture in ultra-scaled devices.
HBs have CTLs in the vicinity of the respective band edges of Si for both electron and hole trapping. Nevertheless, based on the analysis of the formation energies it is shown that HBs are only likely to form at preexisting OVs (distributed around 2 eV at preexisting OV compared to 7 eV in SiO\(_2\) bulk) which heavily limits their concentration. The formation energies further suggest that H-\(E^\prime \) is the most relevant defect candidate for trapping charges, as its formation energy in the bulk system is in a reasonable energy range (\(E_\mathrm {Form} = 2.4\textpm 0.5\) eV) with CTLs near the band edges of the Si substrate, effective for both electron and hole capture. The analysis of the negative charge state shows that by considering only the stable H-\(E^\prime \) \(_{\mathrm {min}}^{-}\) configurations, the H-\(E^\prime \) defects have CTLs for trapping electrons distributed around 1.5\(\textpm \)0.4 eV below the CBM of the Si substrate. Thus, for this defect type, the interaction with electrons from the conduction band edge of Si is suppressed compared to holes from the valence band edge, with both of the \(\varepsilon (0/+1)\) CTLs distributed only around 0.5\(\textpm \)0.5 eV above the VBM of the substrate. The H-\(E^\prime \) can therefore be regarded to contribute to NBTI, as, furthermore, H-\(E^\prime \) defects with CTLs below the VBM of Si also have the lowest formation energies and therefore exist in higher concentrations as well. The comparison between hole and electron capture CTLs gives a good explanation for the suppressed PBTI effect when compared to NBTI observed in MOS devices [31, 235, 236, 208]. By correlating different CTLs of single defects in our multi-state model, it can be seen that two trap levels of the same defect may differ by more than 2 eV. This can directly be linked to different charge capture time constants of single defects observed for example in anomalous random telegraph noise.
The charged energy levels of a defect can be shifted by an applied bias in a MOS structure, altering the Fermi level dependent formation energy and the transition barriers between differently charged configurations. To investigate all occurring charge transitions, relaxation energies were calculated and used as fitting points for potential energy curves (PEC) in the harmonic approximation. By extracting the energy barriers from the CPs of two differently charged PECs, it is shown that energy barriers for single charge transfers vary between 0.1 and 2.5 eV depending on the Fermi level. Furthermore, it was demonstrated that a transition from charge state \(-1\) (\(+1\)) to 0 compared to the direct transition \(-1\) (\(+1\)) to \(+1\) (\(-1\)) is not only much more likely in terms of the vanishing cross section of 3-particle processes but is also always energetically favored. A stable positively charged defect (state 2) is thus highly unlikely to directly transform into the negative charge state (\(2 \rightarrow 3^\prime \)). Instead, the defect preferably either transitions to a meta-stable puckered configuration without charge transfer (\(2 \rightarrow 2^\prime \)) or emits a hole to become neutral (\(2 \rightarrow 1^\prime \)) again. Subsequently, the defect can either once more capture a hole (\(1^\prime \rightarrow 2\)), undergo a charge conserving transition between puckered and unpuckered (\(1^\prime \rightarrow 1\)) or, for the relevant H-\(E^\prime \), finally trap an electron to transform into one of the negatively charged highly unstable configurations (\(1 \rightarrow 3^\prime \)), which quickly relax into H-\(E^\prime \) \(_{\mathrm {min}}^{-}\) (\(3^\prime \rightarrow 3\)). By emitting the extra electron, the H either diffuses away from the defect site (\(3\rightarrow 0\)), potentially creating a new defect at a different position in the oxide, or the defect becomes neutral again (\(3 \rightarrow 1\)), once more able to capture either an electron or a hole from the substrate.