[<] [^] [>] [TOC] Prev: 2 Scope Up: Pyka et al.: Optimized Next: 3.1 Isotropic Etching/Deposition


3 Topography Algorithms

For the topography simulation we use morphological operations derived from image processing [13] described in detail in [14] and [17]. This algorithm proved to be very stable since the cellular representation implicitly avoids the formation of unphysical loops. As symbolized in Fig. 2 for two dimensions the geometry is represented by an array of cubic cells which have a unique material index. A structuring element whose shape depends on the process to be modeled and whose size depends on the local etching or deposition rate is moved along the surface and all cells hit by the element are marked. After each time step, the indices of the material array are updated, the new surface is extracted and again size and orientation of the structuring elements are calculated and applied to the new surface until the overall simulation time is completed.

Figure 2: Schematics of the structuring element algorithm.
\begin{figure}\begin{center} {\resizebox{!}{7cm}{\includegraphics{materials-col.eps}}} \vspace{-5mm} \end{center}\end{figure}

In the general three-dimensional case the structuring element is an ellipsoid with the three diameters $a$, $b$, and $c$. Its orientation is specified by a polar and an azimuthal angle. This general ellipsoid can be used to model reactive ion etching and sputter deposition where the local rate depends on the visibility conditions and is calculated as integral of the particle distribution function over the visible solid angle.

For simple anisotropic models, the main axis of the ellipsoid is fixed to a vertical direction and its size is given by a vertical rate $a$ and a lateral rate $b = c$. For the isotropic case all three diameters are equal $a = b =c$, the ellipsoid merges to a sphere, and the orientation becomes insignificant.

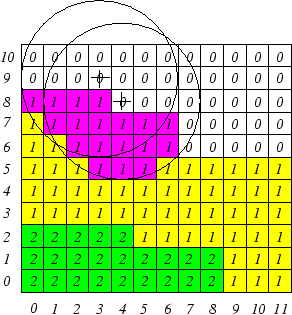
Deposition and etching is modeled in the same way, the difference is that for deposition vacuum cells hit by the structuring element are set to the index of the deposited material whereas for etching marked material cells are removed by setting them to the vacuum index 0. In this sense Fig. 2 shows the two-dimensional equivalent of circles modeling an isotropic process. The purple squares denote material cells hit by the structuring element which will be etched away in this time step.

As can already be seen in Fig. 2, the morphological operations cause unnecessary and redundant operations. Unnecessary operations are performed for the vacuum cells above the surface for etching processes and vice versa for deposition. Redundancy originates from structuring elements applied to adjacent surface cells hitting one and the same cell several times. For larger simulation domains this turns out to be slow because of the dependence of the calculation time on the number of cells. If $n$ is the number of cells per micron, the number of operations on the three-dimensional material array depends on $n^3$. The same applies for the scanning operation of the region surrounding the structuring element when deciding whether a cell is inside the sphere or outside. The calculation time of this second operation additionally increases with the deposition rate $r^3$, because the rate determines the radius of the sphere and thus the volume to be scanned.

Our efforts to reduce such unnecessary and redundant operations and thus to increase the simulation speed for several etching and deposition processes are described in the next sections.


Subsections [<] [^] [>] [TOC] Prev: 2 Scope Up: Pyka et al.: Optimized Next: 3.1 Isotropic Etching/Deposition
W. Pyka, R. Martins, and S. Selberherr: Optimized Algorithms for Three-Dimensional Cellular Topography Simulation