


 |  |  |
While both of the extremes, the quantum setting as well as the classical world in their pure forms are well covered by powerful descriptions with respect to both, theory as well as application, the realm between them remains problematic, since both descriptions are driven to extremes of their validity.
In an attempt to bridge the gap between the two worlds in the setting of solid state physics, the following scheme has been developed which calculates an estimate for the modification of a coherent solution as obtained by quantum mechanics, under the influence of classical scattering.
The following primarily uses the wave vector 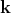 instead of the momentum
instead of the momentum 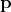 in the descriptions, as is
customary in solid state physics. Furthermore, it may be beneficial to forgo the use of the full structure
as presented in Equation 5.75 in Section 5.7 and decompose the description in the following
manner
in the descriptions, as is
customary in solid state physics. Furthermore, it may be beneficial to forgo the use of the full structure
as presented in Equation 5.75 in Section 5.7 and decompose the description in the following
manner
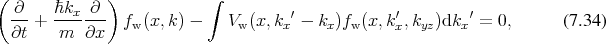
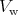 is called the Wigner potential [99][135]. This is the basis for further simplification. Under
the assumption that
is called the Wigner potential [99][135]. This is the basis for further simplification. Under
the assumption that 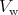 locally varies at most linearly, a classical limit for this expression can be
recovered [136] in the form
locally varies at most linearly, a classical limit for this expression can be
recovered [136] in the form
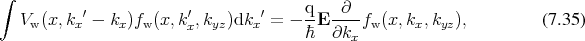
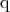 is the charge and
is the charge and 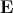 the electric field. Furthermore, the considerations are given here for one
spatial dimension. The remaining two dimensions are assumed to be in equilibrium thus imposing a
form for the coherent Wigner function
the electric field. Furthermore, the considerations are given here for one
spatial dimension. The remaining two dimensions are assumed to be in equilibrium thus imposing a
form for the coherent Wigner function 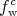 of
of
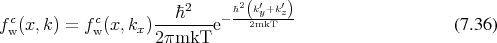
The Wigner Boltzmann equation [137] is obtained by combining elements of Equation 7.34 describing coherent transport and Boltzmann’s equation, as given in Equation 5.38 which includes scattering. The combination of the scattering operator and the coherent quantum expression in one dimension can be given as
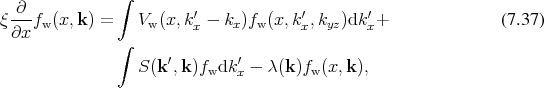
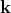 is specifically decomposed into the components
is specifically decomposed into the components 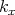 and
and 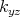 .
.
The deviation 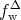 of the true Wigner distribution
of the true Wigner distribution 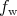 from the purely coherent
from the purely coherent 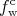 is expressed
as
is expressed
as
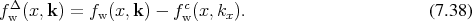
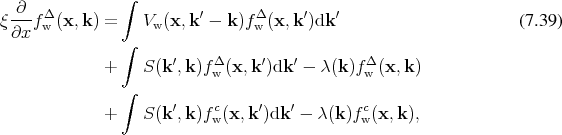
![[ ∂ ] ∫
ξ--- + λ(k) fΔw (x, k) = Vw (x,k ′ − k)fwΔ(x,k ′)dk ′ (7 .40)
∂x ∫
′ Δ ′ ′
+ S (k ,k)fw (x,k )dk
∫
+ S (k′,k)fc(x, k′)dk ′ − λ (k )fc(x,k ),
w w](whole1158x.png)
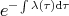 . Thus the integral form of the correction
equation becomes
. Thus the integral form of the correction
equation becomes
![[ ∫0 ]0 ∫ ∫ ∫0
fΔw(x,k)e− t λ(τ)dτ = Vw (x,k′ − k)fΔw (x, k′)dk′e− t λ(τ)dτdt (7.41)
tb ∫[tb,0]∫
′ Δ ′ ′− ∫0λ(τ)dτ
+ S (k ,k )fw (x, k)dk e t dt
∫[tb,0]∫
′ c ′ ′− ∫t0λ(τ)dτ
+ S (k ,k )fw(x,k )dk e dt
∫[tb,0] ∫
− λ (k)fc(x,k )e− 0t λ(τ)dτdt.
[tb,0] w](whole1160x.png)
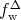 on the
right hand side, which corresponds to keeping only the zeroth order term, the expression
reduces to contain only terms including
on the
right hand side, which corresponds to keeping only the zeroth order term, the expression
reduces to contain only terms including 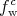 which is assumed to be known from coherent
calculations.
which is assumed to be known from coherent
calculations.
![∫ ∫
fΔw (x, k) = S(k′,k)fcw(x, k′)dk ′e−λ(k)(−t)dt (7.42)
[tb,0]
∫ c −λ(k)(−t)
− λ(k)fw (x,k)e dt
[tb,0]](whole1163x.png)
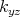 , thus
giving
, thus
giving
![∫ ∫ ∫
Δ ′ c ′ ′−λ(k)(−t)
fw (x,kx) = S (k,k )fw(x,k )dk e dkyzdt (7.43)
∫[tb,0]∫
c −λ(k)(−t)
− [t ,0] λ(k)fw(x,k )e dkyzdt.
b](whole1165x.png)
![∫ ∫ ∫
fΔw (x,kx) = S (k ′,k )fcw(x − vxt,k′)dk′e−λ(k)tdkyzdt (7.44)
∫[0,|tb|]∫
c − λ(k)t
− λ (k)fw(x − vxt,k)e dkyzdt,
[0,|tb|]](whole1166x.png)
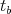 will be
set to correspond to a positive value of the parameter without further particular indication
thereof.
will be
set to correspond to a positive value of the parameter without further particular indication
thereof.
Rearranging and enhancing the last expression to extract representations identifiable as probabilities as was done for the derivations following Equation 7.10 gives
![∫ ∫ ∫ { S(k ′,k )} { }
fΔw(x,kx) = -------- λ(k )e− λ(k)t fwc(x − vxt,k′)dk ′dkyzdt (7.45)
∫ [0,tb]∫ ¯λ (k ′)
{ −λ(k)t} c
− λ(k)e fw(x − vxt,k)dkyzdt,
[0,tb]](whole1168x.png)
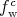 to an estimator corresponding to the point at the end of the trajectory.
to an estimator corresponding to the point at the end of the trajectory.The second integral term lacks the expression for the scattering probability, thus the algorithm can be given as:
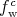 to an estimator corresponding to the point at the end of the trajectory.
to an estimator corresponding to the point at the end of the trajectory.The procedures for both integrals are performed using a subdivision of phase space into a
structured grid, which defines the topology, as discussed in Section 6.3, and an estimator is
associated with every grid node. This grid is then traversed and the two outlined algorithms
are applied starting at every grid node, thus sampling phase space. The initialization of the
electron states at every point has to take into account the decomposition into 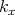 and
and 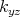 components. Therefore, the
components. Therefore, the 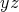 components are initialized assuming equilibrium, while the
components are initialized assuming equilibrium, while the 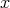 component is initialized corresponding to the phase space position indicated by the grid.
The grid is also used to hold parameters for the trajectories, thus making local modelling
available, as described in Section 6.5. The local scattering mechanisms can reuse the know how
of already existing codes, either directly, by extending the old code base, or by applying
the methodology described in Section 7.2.3 to facilitate incorporation into a new frame
work.
component is initialized corresponding to the phase space position indicated by the grid.
The grid is also used to hold parameters for the trajectories, thus making local modelling
available, as described in Section 6.5. The local scattering mechanisms can reuse the know how
of already existing codes, either directly, by extending the old code base, or by applying
the methodology described in Section 7.2.3 to facilitate incorporation into a new frame
work.
The derived correction is applied to a resonant tunnelling diode (RTD), as it combines quantum mechanical features with classical influence due to scattering. The resonant effect is clearly due to quantum phenomena, yet the dimensions of the device may be such that scattering will disturb any purely coherent solution.
The structure of the device is given Figure 7.8, where the quantum well at the centre of the
device is 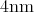 wide. The barriers have a thickness of
wide. The barriers have a thickness of  and a height of
and a height of 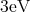 . The
active device is surrounded by several microns of contact region on both sides, where the
distribution of charge carriers is undisturbed by the operation or structure of the device. This
apparently inert region of the device has proved itself to be very important for the accuracy of
the calculations due to the presented algorithm as is demonstrated in the later Figure 7.13.
. The
active device is surrounded by several microns of contact region on both sides, where the
distribution of charge carriers is undisturbed by the operation or structure of the device. This
apparently inert region of the device has proved itself to be very important for the accuracy of
the calculations due to the presented algorithm as is demonstrated in the later Figure 7.13.
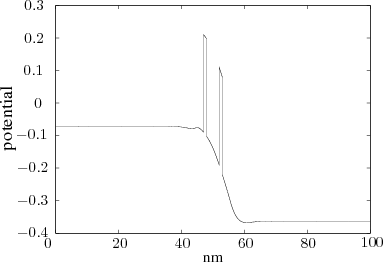
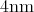 wide quantum well is surrounded
by
wide quantum well is surrounded
by  barriers with a height of
barriers with a height of 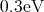 , applied is
, applied is 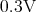 bias.
bias. The derivations critically depend on data corresponding to the coherent quantum case represented by
 . As outlined in Section 5.7 it can be obtained from a density matrix representation by means of
transform as shown in Equation 5.71. This density matrix can be efficiently provided using a
Non-Equilibrium Green’s Function (NEGF) [138][139][140] procedure. After the input has been
subjected to the transformation, thus resulting coherent Wigner function representation serves as direct
input for the Monte Carlo algorithm. An example of the Wigner representation corresponding to an RTD
device is depicted in Figure 7.9.
. As outlined in Section 5.7 it can be obtained from a density matrix representation by means of
transform as shown in Equation 5.71. This density matrix can be efficiently provided using a
Non-Equilibrium Green’s Function (NEGF) [138][139][140] procedure. After the input has been
subjected to the transformation, thus resulting coherent Wigner function representation serves as direct
input for the Monte Carlo algorithm. An example of the Wigner representation corresponding to an RTD
device is depicted in Figure 7.9.

 obtained from transforming the coherent density
matrix provided by a NEGF procedure.
obtained from transforming the coherent density
matrix provided by a NEGF procedure.The stochastic nature of the Monte Carlo approach makes verification and debugging of implementations tedious. Therefore, simple test cases are of great importance to quickly detect and eliminate anomalies. One such possibility presents itself, when recording the length of trajectories, since every point is used to generate a trajectory which is either absorbed at the boundary or terminated by a scattering event, it is expected that trajectories will be shorter in the boundary regions. An investigation using histograms, shows that this is indeed the case as shown in Figure 7.10.
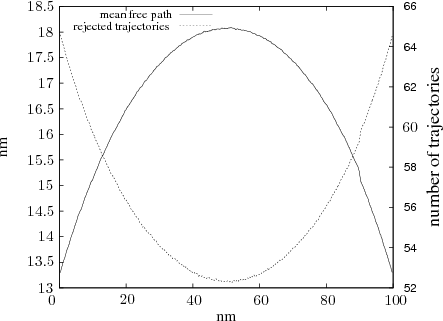
Furthermore, the assumption that the correction is mainly influenced by the first scattering event can be gauged, by continuing the evolution past the first collision and continuing the trajectory, until it reaches a boundary.
Figure 7.11 shows a steep decline in the number of trajectories still continuing within the domain of interest as the number of scattering events increases, corresponding to approximately an order of magnitude per scattering event.
Finally, having established a means to estimate the validity of the assumption of considering only the first order terms the procedure can be applied and the results are presented in Figure 7.12.
The initial concentration, as obtained calculated from the density matrix is adapted by the scattering, increasing the concentration in the quantum well. It should be pointed out, however that this calculation is not self consistent that is the electric field is kept constant throughout the simulation and not updated due to the shift of charge carriers. The procedure can be refined to include such updates, by using the newly obtained distribution to calculate a new electric field and also calculating a new density matrix. This new data can then be reapplied to the same procedure. The importance of adhering to the assumptions used in the theoretical derivations of the Monte Carlo procedure is illustrated in Figure 7.13.
The derivation assumes that the contact regions are in equilibrium, which is not met precisely in the input for the calculation depicted in Figure 7.13. The discrepancy is not visible directly in the given figure, as there is seemingly no disturbance due to the flatness of the contacts. However, applying the derived algorithm reveals that curiously the correction increases in the left contact, which by initial assumption should remain its flat equilibrium configuration. Examining the boundary conditions, revealed a deviation from equilibrium. When correcting this irregularity by extending the bounding contact regions, the results shown in Figure 7.12 are obtained.
 |  |  |