« PreviousUpNext »Contents
Previous: 3.2 Electromigration in Bulk Metals    Top: 3 Models    Next: 3.4 Continuum Mechanical Model

3.3  Electromigration at Interfaces

Interfaces regarding EM are the domains which connect either bulk metal domains of the same metal kind or bulk materials of two different kinds. In the second case the interface can separate two conducting materials or a conducting material from a nonconducting material. In all three cases the interface can have a diffusion coefficient higher then the coefficient of the bulk material or a lower equilibrium concentration.
How to handle this behavior is shown in the two next subsections. This is followed by a subsection explaining the case of an interface between two conducting materials, where the interface can have a segregation behavior.

3.3.1  Fast Diffusivity Paths at Interfaces

The crystal structure is highly disturbed at interfaces as there crystals with different orientations or even crystals with other lattice kinds or lattice parameters meet. This leads to atoms with a decreased binding energy compared to the atoms located in the undisturbed lattice of a bulk material. This increases the probability for those atoms to jump and therefore increases also the diffusion coefficient as shown by Sørensen et al. [133].
This jumping is limited by the two-dimensional plane of the interface embedded in the 3D space. Therefore, interfaces show a highly direction depending diffusion coefficient giving it the form of a second order tensor. Since for interfaces the real thickness can hardly be defined, for simulation normally the interface is modeled by a domain with a small but finite thickness. As a smaller thickness leads to a higher amount of mesh elements to ensure a reasonable mesh quality, a thicker layer is desired. For these reasons in the further description of the modeling of fast diffusivity paths a thickness \( \delta \) is chosen to be the modeled interface thickness and its influence is pointed out.

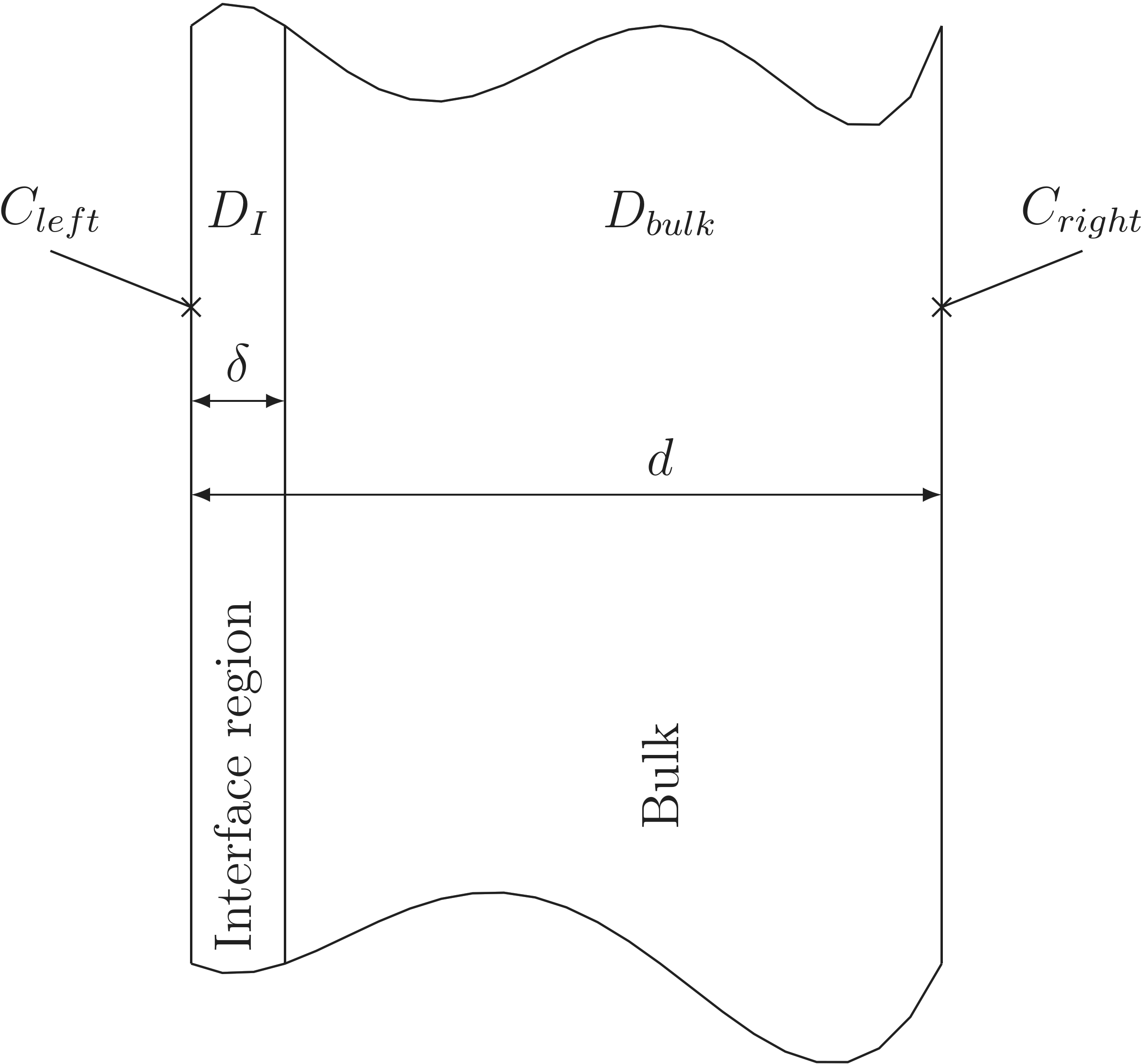
Figure 3.1.:  Segment with an interface domain and a neighboring bulk domain for the diffusion coefficient calculation.

In Section 2.1.3 the effective diffusion coefficient was calculated by (2.9), where the diffusion in the bulk was taken to be negligibly small compared to the diffusion in the \( \mathrm {G}\mathrm {B} \). Extending this equation for a finite diffusion coefficient in the bulk leads to the expression for the effective diffusion coefficient [136] for a structure shown in Figure 3.1 with an interface and an bulk segment.

(3.17) \{begin}{gather} D_{\mathrm {e}\mathrm {f}\mathrm {f}}=\displaystyle \frac {\delta }{d}D_{\mathrm {I}}+\frac {d-\delta }{d}D_{\mathrm {b}\mathrm {u}\mathrm {l}\mathrm {k}} \mathref {(3.17)} \{end}{gather}

If the effective diffusion coefficient is known from experimental data this equation can be rearranged to

(3.18) \{begin}{gather} D_{\mathrm {I}}(\displaystyle \delta )=D_{\mathrm {b}\mathrm {u}\mathrm {l}\mathrm {k}}+\frac {d}{\delta }(D_{\mathrm {e}\mathrm {f}\mathrm {f}}-D_{\mathrm {b}\mathrm {u}\mathrm {l}\mathrm {k}}), \mathref {(3.18)} \{end}{gather}

giving a functional dependence on the interface thickness and the interface diffusion coefficient.
This value is the diffusion coefficient in the directions parallel to the interface surface, whereas the value perpendicular to the interface surface is given by the bulk diffusion coefficient, leading to a tensor form of the diffusion coefficient. For very small interface thicknesses this distinction of the direction is not needed, shown by the following gedankenexperiment. The flow of vacancies perpendicular to the interface is calculated for the structure shown in Figure 3.1 for predetermined vacancy concentrations at the left and right side of the structure in the following way:

(3.19) \{begin}{gather} J_{\mathrm {D}}=D\displaystyle \frac {\partial C_{v}}{\partial x} \mathref {(3.19)} \{end}{gather}

left

(3.20) \{begin}{gather} \triangle C_{v} = C_{v,right} - C_{v,left} = \displaystyle \int \displaystyle \frac {J}{D(x)}\mathrm {d}x \mathref {(3.20)} \{end}{gather}

right
For the case of an infinite small interface \( (\delta \rightarrow 0) \) this leads to

(3.21) \{begin}{gather} \displaystyle \triangle C_{v,\delta \rightarrow 0}=J_{\delta \rightarrow 0}\frac {d}{D_{\mathrm {b}\mathrm {u}\mathrm {l}\mathrm {k}}}, \mathref {(3.21)} \{end}{gather}

whereas for a finite interface it results in

(3.22) \{begin}{gather} \displaystyle \triangle C_{v,\delta }=J_{\delta }\ \Bigl (\frac {d-\delta }{D_{\mathrm {b}\mathrm {u}1\mathrm {k}}}+\frac {\delta }{D_{\mathrm {I}}}\Bigr ) . \mathref {(3.22)} \{end}{gather}

Setting both equations to the concentration difference assumed at the beginning, substituting \( D_{\mathrm {I}} \) form (3.18) and calculating the relative error gives

(3.23) \{begin}{gather} \displaystyle \epsilon =\frac {J_{\delta }+J_{\delta \rightarrow 0}}{J_{\delta \rightarrow 0}}=\ \frac {\delta (D_{\mathrm {e}\mathrm {f}\mathrm {f}}-D_{\mathrm {b}\mathrm {u}\mathrm {l}\mathrm {k}})}{d(-D_{\mathrm {e}\mathrm {f}\mathrm {f}}+D_{\mathrm {bulk}})+\delta (D_{\mathrm {e}\mathrm {f}\mathrm {f}}-2D_{\mathrm {b}\mathrm {u}\mathrm {l}\mathrm {k}})}, \mathref {(3.23)} \{end}{gather}

and establishes a rule under which the directional dependence of the diffusion can be neglected.

3.3.2  Interfaces with Lower Equilibrium Concentrations

Interfaces can have, due to their disorder, a lower vacancy equilibrium concentration, as in the bulk, where vacancies can be easily filled by surrounding atoms as their binding energy is lower there. This is modeled by an extra region with a lower equilibrium concentration between the bulk materials in the Rosenberg-Ohring term inside the domain in contrast to the surrounding domains. This phenomenon is particularly important at interfaces between voids and bulk materials, as there at one side a lattice is formed, whereas on the other side no material is present. Therefore, this behavior is given special attention in the phase field model for voids in Section 3.6.

3.3.3  Segregation Model

Surfaces between different conducting materials play a special role in EM. The current at these interfaces passes from one conducting material to another. But for vacancies passing the interface can be hindered leading to a segregation in the vicinity of those interfaces. The segregation at interfaces was modeled by Lau et al. [90] based on the work of Grove et al. [52]. The interface in this model makes use of a trap density \( T, \) where the filled traps are denoted by \( T_{\mathrm {d}} \) and the empty ones by \( T_{0} \). These traps are dynamically coupled to the bulk materials’ concentrations \( C_{1} \) and \( C_{2} \) by the flows

(3.24) \{begin}{gather} F_{1}=t_{1}T_{0}C_{1}-e_{1}T_{\mathrm {d}} \mathref {(3.24)} \{end}{gather}

and

(3.25) \{begin}{gather} F_{2}=t_{2}T_{0}C_{2}-e_{2}T_{\mathrm {d}}, \mathref {m(3.25)} \{end}{gather}

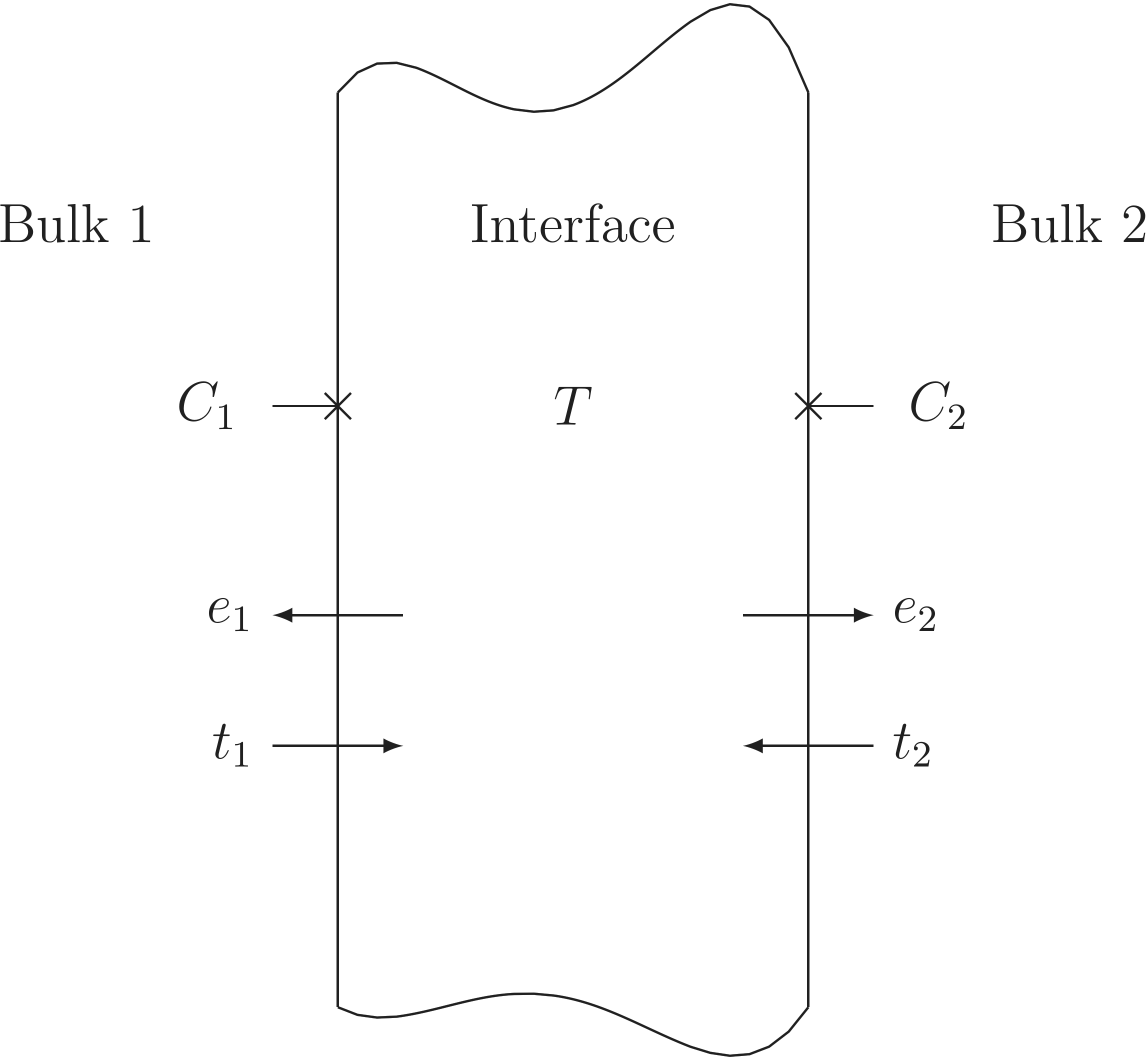
Figure 3.2.:  Schematics for the derivation of the segregation model according to [90].

respectively, where the \( e_{i} \) are the emission probabilities and \( t_{i} \) are the trapping probabilities. These equations can be put together to calculate the time derivative of the filled trap density \( T_{\mathrm {d}} \) by

(3.26) \{begin}{gather} \displaystyle \frac {\partial T_{\mathrm {d}}}{\partial t}=F_{2}+F_{1}=t_{2}T_{0}C_{2}-e_{2}T_{\mathrm {d}}+t_{1}T_{0}C_{1}-e_{1}T_{\mathrm {d}}. \mathref {(3.26)} \{end}{gather}

With the assumption of an equilibrium, where the filled trap density is constant in time, (3.26) can be rearranged to

(3.27) \{begin}{gather} T_{0}(t_{2}C_{2}+t_{1}C_{1})=T_{\mathrm {d}}(e_{2}+e_{1}). \mathref {(3.27)} \{end}{gather}

Using the fact that the filled and the empty traps are the sum of the total traps density

(3.28) \{begin}{gather} T=T_{\mathrm {d}}+T_{0}, \mathref {(3.28)} \{end}{gather}

leads to the filled trap density

(3.29) \{begin}{gather} T_{\mathrm {d}}=\displaystyle \frac {T(C_{1}+C_{2}\alpha )}{C_{1}+C_{2}\alpha +\beta }, \mathref {(3.29)} \{end}{gather}

where \( \alpha \) and \( \beta \) are given by

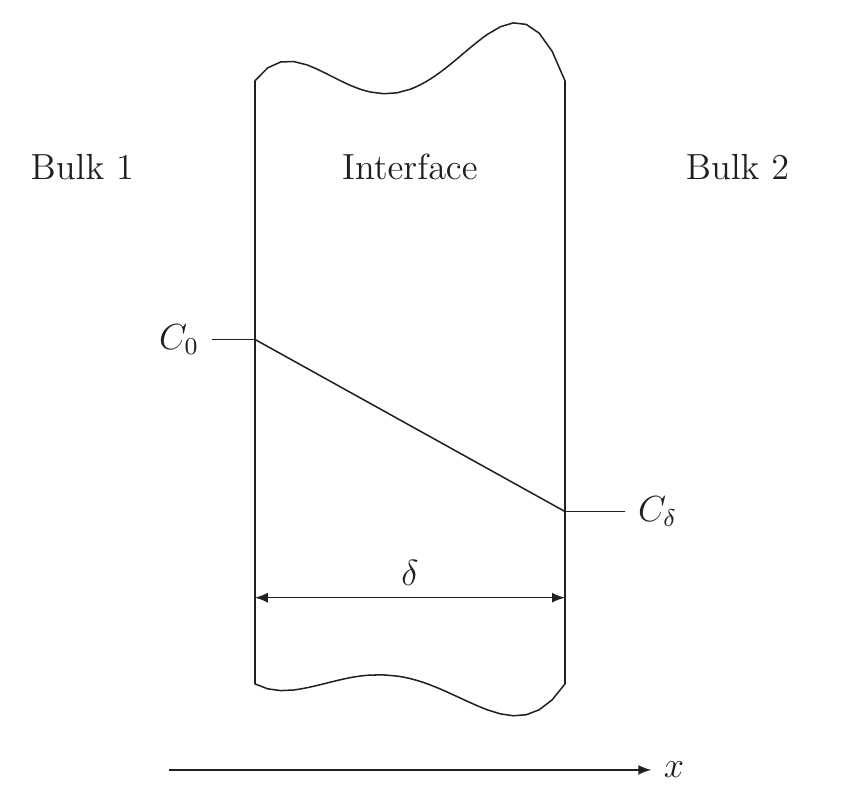
(3.30) \{begin}{gather} \alpha =\frac {t_{2}}{t_{1}} \mathref {(3.30)} \{end}{gather}

(3.31) \{begin}{gather} \displaystyle \beta =\ \frac {e_{1}+e_{2}}{t_{1}}. \mathref {(3.31)} \{end}{gather}

Figure 3.3.:  Schematics for the derivation of the segregation model as an infinite thin representation of an interface with \( \delta \) thickness.

Inserting the filled trap density in the flow equations (3.24) and (3.25) keeping in mind (3.28) results in

(3.32) \{begin}{gather} F=F_{1}=-F_{2}=T\displaystyle \frac {t_{1}e_{2}}{t_{1}C_{1}+t_{2}C_{2}+e_{2}+e_{1}} (C_{1}-\displaystyle \frac {e_{1}t_{2}}{e_{2}t_{1}}C_{2}) =h(C_{1}-mC_{2}), \mathref {(3.32)} \{end}{gather}

with \( h \) named the transport coefficient, and \( m \) the segregation coefficient. In the calculations the segregation coefficient is taken to be constant.

In the following it is shown that the segregation model can also be used for an infinitely thin representation of a domain with a thickness \( \delta \) and a diffusion coefficient \( D_{\mathrm {I}} \), if \( m \) is set to one. As the domain thickness is small compared to a characteristic length (e.g. grain radius) the concentration profile in this thin domain can be approximated with the first order Taylor expansion (\( \mathrm {c}.\mathrm {f} \). Figure 3.3)

(3.33) \{begin}{gather} C(x)=C_{0}+\displaystyle \frac {x}{\delta }(C_{\delta }-C_{0}), \mathref {(3.33)} \{end}{gather}

where \( C_{0} \) can be identified as the concentration in the left bulk material equaling \( C_{1} \) and \( C_{\delta } \) as the concentration in the right bulk material \( C_{2} \). Differentiation of (3.33) with respect to \( x \) and putting the result in the flux driven by diffusion (cf. (3.11)) regarding only the \( x \) direction leads to

(3.34) \{begin}{gather} J_{\mathrm {D},2\rightarrow 1}=\displaystyle \frac {D_{\mathrm {I},x}}{\delta }(C_{2}-C_{1}), \mathref {(3.34)} \{end}{gather}

giving exactly the result of the segregation model shown above. It should be emphasized that this interface has in the limit of an infinitely small thickness no capability to store any vacancies, as all the flow from the left side is compensated by an equal flow on the right side. This behavior has to be taken into account as for mechanical stress calculations in FEM there is no easy way to handle a volume decrease due to the pile-up of vacancies in infinitely thin interfaces exhibiting zero volume.

« PreviousUpNext »Contents
Previous: 3.2 Electromigration in Bulk Metals    Top: 3 Models    Next: 3.4 Continuum Mechanical Model