



Next: Publications
Up: Peter Fleischmann's Dissertation
Previous: Bibliography
- 2.1. Medial axis and medial object, M. Price et al. [124].
- 2.2. Thin layers in two and three dimensions with the local
feature size (radius of the circles/spheres) at example
locations (stars).
- 3.1. Various types of not so well shaped elements and some
parameters.
- 3.2. The relation between the edge length and its opposite angle in a
triangle follows from
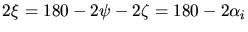 and therefore
and therefore
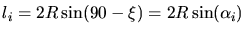 .
.
- 3.3. With constant edge length and circumsphere radius the opposite
dihedral angle in a tetrahedron can have arbitrary values.
- 3.4. A Voronoi box which intersects the boundary and an
outside Voronoi point
 . The Voronoi regions for each point
are shaded differently.
. The Voronoi regions for each point
are shaded differently.
- 3.5. Finite element mesh criterion for two dimensions.
- 3.6.
 tessellation and Crit. 3.3.
tessellation and Crit. 3.3.
- 3.7.
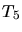 tessellation, no obtuse dihedral angles.
tessellation, no obtuse dihedral angles.
- 3.8. Global stiffness matrix for a
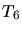 tessellation and local
matrices of those four elements which are adjacent to edge
tessellation and local
matrices of those four elements which are adjacent to edge 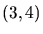 .
.
- 3.9.
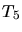 type tessellation with a shifted point.
type tessellation with a shifted point.
- 3.10. Element matrices which contribute to the entry in the global
stiffness matrix for the edge
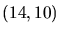 . Due to the symmetry of the
mesh the three matrices on the left and on the right side possess
the same entries.
. Due to the symmetry of the
mesh the three matrices on the left and on the right side possess
the same entries.
- 3.11. Delaunay mesh (
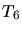 ), 3072 tetrahedra.
), 3072 tetrahedra.
- 3.12. Delaunay mesh (
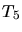 ), 2560 tetrahedra.
), 2560 tetrahedra.
- 3.13. Non-Delaunay mesh, 2560 tetrahedra.
- 3.14. Red-Green refinement using mixed elements in three dimensions.
- 3.15. 3-2 or 2-3 local transformation. The internal facet which is
being swapped is drawn shaded.
- 3.16. Splitting an edge to ensure a well connected surface
topology. Correctly splitting a polygon requires an expensive
calculation of all intersections.
- 3.17. Staircase effects approximate slopes and result in unnecessary
large meshes.
- 3.18. Marching cubes algorithm applied to discrete data which
describes the distribution of a finite number of materials.
- 3.19. Pathological cases and alternative templates.
- 3.20. Detail of a trench consisting of 2912 triangles before and 288
triangles after data reduction by locally discarding points.
- 4.1. Unstructured quadrilateral surface mesh, MENTAT II
[98].
- 4.2. LOCOS: (a) structured mesh, 2000 tetrahedra (b) unstructured
mesh, 957 tetrahedra.
- 4.3. Overlaying two layer descriptions and lateral two-dimensional
unstructured mesh.
- 4.4. Layout structure description.
- 4.5. Interconnect simulation of a part of the layout using a
layer-based product mesh.
- 4.6. Intersection of the cartesian cells with the boundary, M. Berger
et al. [2].
- 4.7. Intersection based octree mesh of Flash EEPROM, ISE ETH
[52].
- 4.8. Various situations in two dimensions and different patterns
depending on the angle
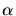 .
.
- 4.9. Three necessary tests to avoid collisions in three
dimensions. The arrows show the direction of the advancing front
and the tetrahedron which is tested and built.
- 4.10. Boundary mesh of the floating gate structure, 36 tetrahedra.
- 5.1. Each Voronoi box associated with a point is differently
shaded. Two triangles
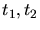 with their circumcenters
with their circumcenters
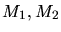 which are the vertices of the Voronoi boxes are depicted for
the correct Delaunay case and for the non-Delaunay case. Incorrect
Voronoi boxes which are derived from non-Delaunay triangles overlap.
which are the vertices of the Voronoi boxes are depicted for
the correct Delaunay case and for the non-Delaunay case. Incorrect
Voronoi boxes which are derived from non-Delaunay triangles overlap.
- 5.2. The Delaunay edge (a) and Delaunay triangle (b) criteria.
- 5.3. (a) Boundaries which are not conform with the Delaunay
Triangulation (b) A constrained Delaunay Triangulation (c) A
conforming Delaunay Triangulation
- 5.4. A constrained Delaunay Triangulation with a non-Delaunay edge
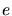 . The point
. The point 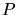 does not affect edge
does not affect edge 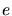 . The half of the smallest
sphere which lies inside the mesh is highlighted.
. The half of the smallest
sphere which lies inside the mesh is highlighted.
- 5.5. An untetrahedralizable twisted prism where the diagonals of
the three side facets almost intersect.
- 5.6. Steiner point insertion at the circumcenter, removal of
non-Delaunay elements, and triangulation of the resulting cavity.
- 5.7. Delaunay Triangulation vs. quality improved Steiner
Triangulation. The original 130 triangles (94 points) were
refined with 128 Steiner points resulting in 376 triangles.
- 5.8. The worst case element with a
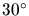 angle and minimum
edge length
angle and minimum
edge length 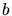 . The largest circumcircle has radius
. The largest circumcircle has radius 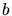 .
.
- 5.9. A naive approach where the bisection of boundary edges and the
insertion of circumcenters runs into an endless loop. The small angle
which causes the insertion of a Steiner point at the center of the
dotted circumcircle is shaded. A better solution can be obtained and
is shown in the bottom left corner.
- 5.10. (a) Non-Delaunay sliver with circumsphere and two adjacent
tetrahedra in the back (b) Strict sense Delaunay sliver with an empty
circumsphere (c) Delaunay sliver with a cospherical point set.
- 6.1. Overall concept
- 6.2. Finite octree point generation.
- 6.3. Mesh for the octree point distribution, 25253 tetrahedra.
- 6.4. A triangle which is at first not flip-able and the state of flip
saturation.
- 6.5. Multiple connected edges.
- 6.6. Non-convex coplanar triangles. The common edge is
by definition flip-able, while the triangles are not.
- 6.7. Refinement types for structural edges.
- 6.8. Refining structural edges for the trivial case of a
planar polygon.
- 6.9. Double sphere criterion.
- 6.10. Locating the triangle which contains the projection of the
circumcenter and flipping of the non-structural edge.
- 6.11. Polygonal boundary description of a MOS Transistor with a
spacer.
- 6.12. Structural edges of the MOS transistor example.
- 6.13. Delaunay surface triangulation.
- 6.14. Adapted surface mesh after Steiner point insertions.
- 6.15. Modified advancing front algorithm.
- 6.16. The triangle to which the next tetrahedron is attached is
shaded for each step.
- 6.17. A snapshot of the growing mesh generated by the modified
advancing front algorithm.
- 6.18. A non-uniform point bucketing scheme and a rectangular search
region which is aligned with the bounding box and which is associated
with a circle and a given
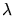 value (two-dimensional analogy).
value (two-dimensional analogy).
- 6.19. Every found point
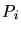 in the search region defines a
in the search region defines a
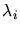 .
.
- 6.20. The scope of
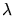 for the two-dimensional case. Depending
on the location of a point its
for the two-dimensional case. Depending
on the location of a point its 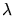 value can reach a critical
value. Singular regions of
value can reach a critical
value. Singular regions of 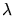 are indicated.
are indicated.
- 6.21. An open surface description and the growing mesh.
- 6.22. Complete boundary representation after tetrahedralization.
- 6.23. Runtime on an HP 9000-735/100Mhz
- 6.24. (a) Overlapping triangles which share two points (b) Only one
common point (c) No points are shared (d) The convex local sphere
boundary, LSPB
- 6.25. Possible error in a three-dimensional tetrahedralization of a
cospherical point set.
- 6.26. Approximately cospherical points can form unexpected
constellations.
- 6.27. The advancing front of the global queue does not pass through
a subset of cospherical points.
- 6.28. (a) One adjacent triangle to merge (b) Of two adjacent
triangles only one can be merged correctly (c),(d) No adjacent
triangles exist
- 6.29. A twisted prism with cospherical vertices and three cocircular
point subsets. It can be converted into a convex polyhedron or into
an untetrahedralizable polyhedron while keeping the vertices
cospherical. Thus, in all cases all triangles satisfy the Delaunay
criterion.
- 7.1. The advancing front at several moments during the meshing
process. It separates the meshed region from the empty parts
of the volume.
- 7.2. Surface mesh of Beethoven's bust.
- 7.3. Structural edges form a contour plot.
- 7.4. The model of a cow.
- 7.5. The mesh of a cow with 11608 elements.
- 7.6. Edges and points of the final mesh.
- 7.7. Final mesh of Beethoven's bust with 17665 elements.
- 7.8. Human skull, mesh with 28512 elements.
- 7.9. Crossections of the human skull mesh.
- 7.10. Structure of the discretized conductors in a DRAM (
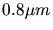 x
x 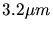 ).
).
- 7.11. Mesh generated with the layer-based method, 6480
tetrahedra. The vertical propagation of refinement through all layers
can be observed.
- 7.12. Fully unstructured Delaunay mesh of the DRAM, 5290 tetrahedra.
- 7.13. Silicon bulk (5139 elements) and four metal lines (51682
elements).
- 7.14. Oxide layer, 47203 elements.
- 7.15. Flow diagram for the high pressure CVD model.
- 7.16. A cylindrical via, mesh with 7324 elements
- 7.17. A cross-section of a cylindrical via with a uniform mesh point
distribution, 7324 elements.
- 7.18. The cross-section of the same cylindrical via meshed
differently shows the non-uniform distribution of mesh points, 75720
elements.
- 7.19. The volume meshes used for the continuum transport model and the
corresponding three-dimensional film profiles for a sequence of time steps of
a Ti/TiN/W plug fill process. The profiles show from bottom to
top the initial circular via, the PVD TiN layer formed by sputter
deposition and the CVD tungsten layer.
- 7.20. Iso surfaces of the
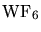 concentration in a damascene
structure, mesh with 18148 elements.
concentration in a damascene
structure, mesh with 18148 elements.
- 7.21. Structural edges.
- 7.22. NMOS Transistor with a thin oxide layer.
- 7.23. Boron implantation profile, mesh with 134374 elements.
- 7.24. Typical CMOS inverter structure with two transistors.
- 7.25. Initial coarse mesh of the CMOS device.
Peter Fleischmann
2000-01-20