3 Dopant Activation
This chapter will discuss key contributions made to modeling and understanding of dopant activation mechanisms in SiC, in particular, a model to predict activation ratios as well as a semi-empirical and a transient activation model. But first, fundamentals of the dopant activation process are introduced in the following.
Semiconductor impurities can be either unintentional, due limited quality control of fabrication steps, or intentional, to provide free charge carriers and to specifically design the electrical properties of the semiconductor material. The intentional introduction of impurities into an intrinsic semiconductor is called doping. In order to generate free carriers in a semiconductor, it is necessary for the implanted impurities to donate electrons to the conduction band (in which case they are called donors) or to provide holes to the valence band (in which case they are called acceptors) [15].
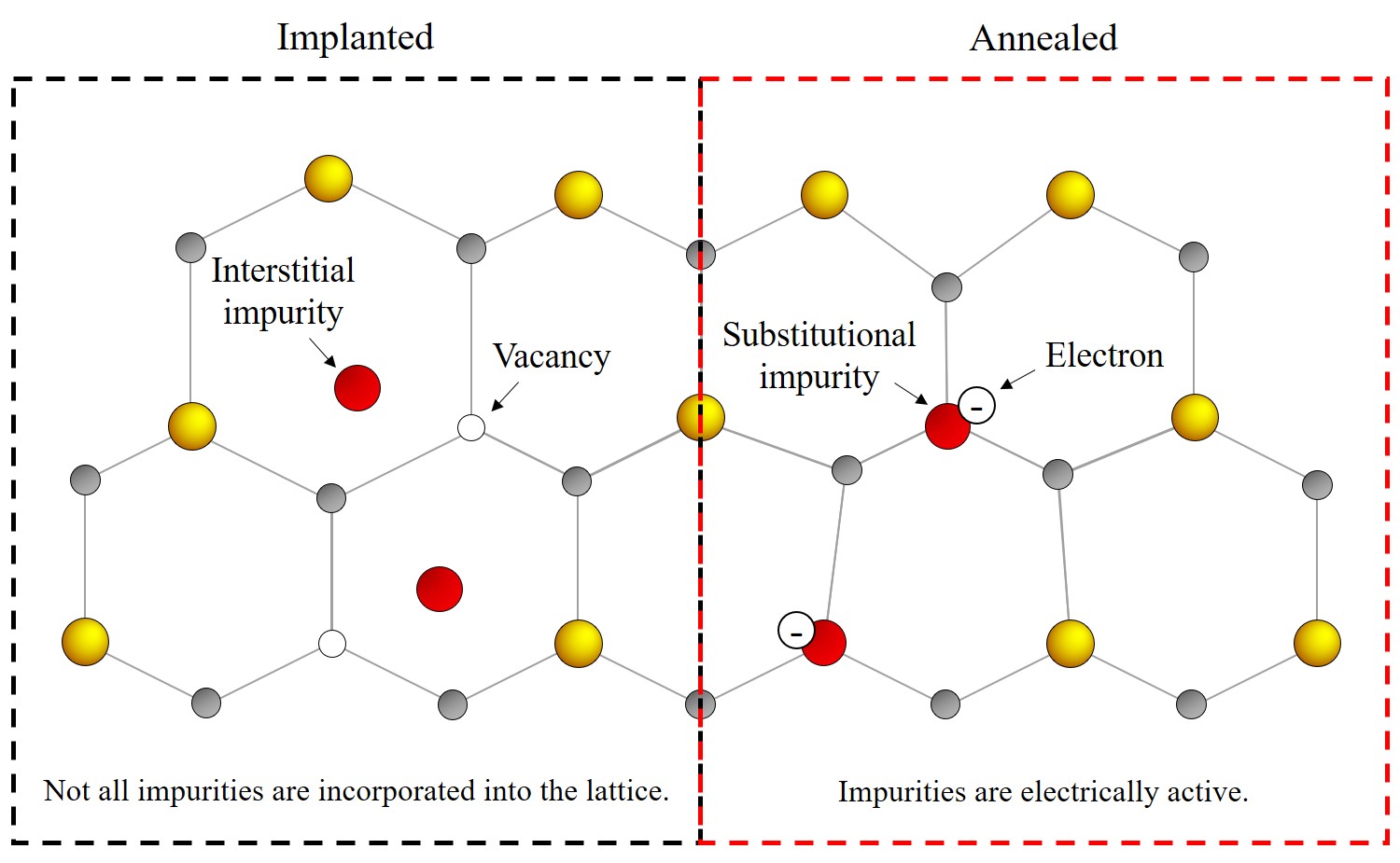
A typical doping technique for SiC applications is ion implantation [128], which must be followed by other processing steps in order to activate the implanted dopants. The activation typically takes place during a thermal annealing step, which is typically performed at elevated temperatures (900-2200°C, in order to eliminate vacancy defects by facilitating the movement of impurity species from interstitial to substitution lattice sites, as shown in Figure 3.1. Moreover, the amorphization damage from implantation is repaired during the annealing step, consequently, the crystal structure is recrystallized [129].
Impurities are divided in two groups, namely shallow and deep impurities. The ionization of shallow impurities typically requires energy levels in the order of the thermal energy (kBT) or less. Deep impurities, however, require significantly more energy than the thermal energy to ionize, which means that only a fraction of the impurities present in a semiconductor will contribute free carriers. Deep impurities, which are more than five times the thermal energy (> 5 · kBT) away from either band edge, are very unlikely to be ionized. These are called traps and can be effective recombination centers in which carriers (electrons and holes) annihilate each other [15].
Impurity doping in SiC is primarily accomplished through the introduction of N and P for n-type and Al and B for p-type doping. The properties of these dopants are shown in Table 3.1. Dopants in SiC incorporate themselves into either cubic (k) or hexagonal (h) lattice sites [130]. 4H-SiC includes an equal number of cubic and hexagonal sites which experience different surroundings and therefore enforce various activation energies.
Table 3.1: Chemical properties of typical SiC dopants. p and n stand for acceptor- and donor-type doping, respectively.
| Element | Symbol | Group | Relative Mass | Doping Type |
| Aluminium | Al | 3 | 26.98 | p |
| Boron | B | 3 | 10.81 | p |
| Nitrogen | N | 5 | 14.01 | n |
| Phosphorus | P | 5 | 30.97 | n |
3.1 Fundamentals of Carrier Concentration
In order to investigate electrical properties of SiC, its doping levels, and activation of implanted species, it is necessary to understand fundamental aspects of carrier concentration in semiconductors. As mentioned above, shallow impurities are ionized with energies ≈ kBT, for which it can be assumed that the ionization of impurities is always 100% [24]. This implies that the free carrier concentration approximately equals the impurity concentration. Therefore, for donors the electron concentration n equals the donor concentration ND
\( \seteqsection {3} \)
\begin{equation} n \approx N_\mathrm {D} \end{equation}
and for acceptors the hole concentration p equals the acceptor concentration NA
\( \seteqsection {3} \) \( \seteqnumber {2} \)
\begin{equation} p \approx N_\mathrm {A}. \end{equation}
In compensated semiconductors the carrier concentration is approximately equal to the difference between the donor and acceptor concentration [131]. For donors this yields
\( \seteqsection {3} \) \( \seteqnumber {3} \)
\begin{equation} n \approx N_\mathrm {D} - N_\mathrm {A} \mathrm {, if } N_\mathrm {D} > N_\mathrm {A} \end{equation}
and for acceptors
\( \seteqsection {3} \) \( \seteqnumber {4} \)
\begin{equation} p \approx N_\mathrm {A} - N_\mathrm {D} \mathrm {, if } N_\mathrm {A} > N_\mathrm {D}. \end{equation}
3.1.1 General Analysis of Impurities
Here a so called general analysis is considered, which in contrary to a regular analysis takes into account that ionization of impurities is not always 100%, as for deep impurities, but is rather given by the impurity distribution function [132]. The general analysis of incomplete impurity ionization assumes no net charge in semiconductors. This implies that the total concentration of positively charged particles (holes or ionized donors ND+) must equal the total concentration of negatively charged particles (electrons or ionized acceptors NA-), such that
\( \seteqsection {3} \) \( \seteqnumber {5} \)
\begin{equation} n + N_\mathrm {A}^{-} = p + N_\mathrm {D}^{+}. \label {eq:neu} \end{equation}
In order to obtain expressions for the carrier concentrations we have to integrate the density of states multiplied with the corresponding carrier distribution function over the energy space [51]. The electron concentration is thus
\( \seteqsection {3} \) \( \seteqnumber {6} \)
\begin{equation} n = \int _{E_\mathrm {C}}^{\infty } \rho _\mathrm {C}(E) \cdot f_\mathrm {D} \cdot dE, \label {eg:n} \end{equation}
where EC is the bottom edge of the conduction band, ρC is the density of states in the conduction band, and fD the distribution function for donors. Similarly, the hole concentration is
\( \seteqsection {3} \) \( \seteqnumber {7} \)
\begin{equation} p = \int _{-\infty }^{E_\mathrm {V}} \rho _\mathrm {V}(E) \cdot f_\mathrm {A} \cdot dE, \label {eg:p} \end{equation}
where EV is the top edge of the valence band, ρV is the density of states in the valence band, and fA the distribution function for acceptors.
The concentration of carriers is obtained by integrating the density of states per unit energy over all possible energies within a band. The density of states in a semiconductor is obtained by solving the Schrödinger equation for the particles in the semiconductor using the simple particle-in-a box model [24]. This model assumes that the particle is free to move within the material and that the band structure is parabolic and isotropic [51]. For an electron which behaves as a free particle with an effective mass me* and Planck constant h, the density of states in the conduction band is given by [133]
\( \seteqsection {3} \) \( \seteqnumber {8} \)
\begin{equation} \rho _\mathrm {C} = \frac {8 \pi \sqrt {2}}{h^{3}} m_\mathrm {e}^{* 3/2} \sqrt {E-E_\mathrm {C}} \mathrm { for } E \geq E_\mathrm {C}. \label {eg:g_C} \end{equation}
The effective mass of electrons for density of state calculations is \(m_\mathrm {e}^{*} = \sqrt [3]{m_\mathrm {M} m_\mathrm {K} m_\mathrm {L}}\). mM and mK are the effective masses in directions perpendicular to the c-axis and mL is the effective mass in direction along the hexagonal c-axis in the Brillouin zone. For a hole, which behaves as a free particle with the effective mass of holes mh*, the density of states in the valence band is given by
\( \seteqsection {3} \) \( \seteqnumber {9} \)
\begin{equation} \rho _\mathrm {V} = \frac {8 \pi \sqrt {2}}{h^{3}} m_\mathrm {h}^{* 3/2} \sqrt {E_\mathrm {V}-E} \mathrm { for } E \leq E_\mathrm {C}, \label {eg:g_V} \end{equation}
The effective mass of holes for density of states calculations is \(m_\mathrm {h}^{*} = \sqrt [3]{m_\mathrm {M} m_\mathrm {K} m_\mathrm {L}}\).
The thermal energy and the position of the impurity level within the bandgap affects the ionization of the impurities. Statistical thermodynamics is used to obtain the probability of the ionization of the impurities, described with the modified Fermi-Dirac distribution function [132]. A filled donor energy level contains only one electron, which can have either spin up or spin down, while having two electrons with opposite spin in one level is not allowed. A distribution function for donors is thus
\( \seteqsection {3} \) \( \seteqnumber {10} \)
\begin{equation} f_\mathrm {D} = \frac {1}{1 + g_\mathrm {D} e^{\frac {E_\mathrm {F} - E_\mathrm {D}}{k_\mathrm {B} T}}}, \end{equation}
where gD is the spin degeneracy factor of donors, EF the Fermi level, ED ionization energy of donors, kB the Boltzmann constant, and T the absolute temperature. On the other hand, the distribution function for acceptors differs due to the two-fold degenerate valence band of SiC, thus the function is given by
\( \seteqsection {3} \) \( \seteqnumber {11} \)
\begin{equation} f_\mathrm {A} = \frac {1}{1 + g_\mathrm {A} e^{\frac {E_\mathrm {A} - E_\mathrm {F} }{ k_\mathrm {B} T}}}, \end{equation}
where gA is the spin degeneracy factor of acceptors and EA the ionization energy of acceptors.
Both of these apply in general for degenerate (i.e., heavily doped) semiconductors. However, non-degenerate semiconductors are lightly doped semiconductors, which by definition follow the approximation that the Fermi energy is at least 3kBT away from either the valence or the conduction band edge. This definition allows for a replacement of the Fermi distribution function with a simpler exponential function, i.e., the Maxwell-Boltzmann distribution function [133]. The distribution function for donors in non-degenerate semiconductors is thus
\( \seteqsection {3} \) \( \seteqnumber {12} \)
\begin{equation} f_\mathrm {D} = e^{\frac {E_\mathrm {F} - E_\mathrm {D} }{k_\mathrm {B} T}} \label {eq:f_D} \end{equation}
and for acceptors
\( \seteqsection {3} \) \( \seteqnumber {13} \)
\begin{equation} f_\mathrm {A} = e^{\frac {E_\mathrm {A} - E_\mathrm {F}}{k_\mathrm {B} T}}. \label {eq:f_A} \end{equation}
The electron concentration can be now analytically solved by integrating (3.6) over all possible states, i.e., from the bottom of the conduction band to infinity
\( \seteqsection {3} \) \( \seteqnumber {14} \)
\begin{equation} n \cong \int _{E_\mathrm {C}}^{\infty } \frac {8 \pi \sqrt {2}}{h^{3}} m_\mathrm {e}^{* 3/2} \sqrt {E-E_\mathrm {C}} \ e^{\frac {E_\mathrm {F}-E}{k_\mathrm {B} T}} dE. \end{equation}
The approximate solution of the integral for electrons is thus
\( \seteqsection {3} \) \( \seteqnumber {15} \)
\begin{equation} n \cong N_\mathrm {C} e^{\frac {E_\mathrm {F}-E_\mathrm {C}}{k_\mathrm {B}T}}, \end{equation}
where NC is the effective density of states in the conduction band [50]
\( \seteqsection {3} \) \( \seteqnumber {16} \)
\begin{equation} N_\mathrm {C} = 2 M_\mathrm {C} \left ( \frac {2 \pi m_\mathrm {e}^{*} k_\mathrm {B} T}{h^{2}} \right )^{3/2}. \end{equation}
MC is the number of equivalent minima in the conduction band. Similarly for the holes, (3.7) is written as
\( \seteqsection {3} \) \( \seteqnumber {17} \)
\begin{equation} p \cong \int _{-\infty }^{E_\mathrm {V}} \frac {8 \pi \sqrt {2}}{h^{3}} m_\mathrm {h}^{* 3/2} \sqrt {E_\mathrm {V}-E} \ e^{\frac {E-E_\mathrm {F}}{k_\mathrm {B} T}} dE. \end{equation}
The analytical solution of the integral for holes is thus
\( \seteqsection {3} \) \( \seteqnumber {18} \)
\begin{equation} p \cong N_\mathrm {V} e^{\frac {E_\mathrm {V}-E_\mathrm {F}}{k_\mathrm {B} T}}, \end{equation}
where NV is the effective density of states in the valence band [50]
\( \seteqsection {3} \) \( \seteqnumber {19} \)
\begin{equation} N_\mathrm {V} = 2 \left ( \frac {2 \pi m_\mathrm {h}^{*} k_\mathrm {B} T}{h^{2}} \right )^{3/2}. \end{equation}
3.1.2 Charge Neutrality Equation
The analysis of the non-degenerate two-type semiconductors can be further expanded with the assumption that an intrinsic carrier concentration is much smaller than the doping concentration and that the compensating acceptors (donors) are fully ionized, i.e., NA+ = NA (ND+ = ND). This assumption yields the very well known charge neutrality equation with the Boltzmann approximation [50] for n-type doping
\( \seteqsection {3} \) \( \seteqnumber {20} \)
\begin{equation} n = N_\mathrm {D}^{+} - N_\mathrm {A}^\mathrm {cp} = \frac {N_\mathrm {D}}{1 + n \frac {g_\mathrm {D}}{N_\mathrm {C}} e^{\frac {E_\mathrm {D}}{k_\mathrm {B} T}} } - N_\mathrm {A}^\mathrm {cp}, \label {eq:cne-n} \end{equation}
where NAcp is the concentration of the compensating acceptors. Similarly, the charge neutrality equation for p-type doping is
\( \seteqsection {3} \) \( \seteqnumber {21} \)
\begin{equation} p = N_\mathrm {A}^{-} - N_\mathrm {D}^\mathrm {cp} =\frac {N_\mathrm {A}}{1 + p \frac {g_\mathrm {A}}{N_\mathrm {V}} e^{\frac {E_\mathrm {A}}{k_\mathrm {B} T}} } - N_\mathrm {D}^\mathrm {cp}, \label {eq:cne-p} \end{equation}
where NDcp is the concentration of the compensating donors.
The implicit expressions (3.20) and (3.21) can be simplified to explicit expressions via the solution of the quadratic equation. The derivative of the charge neutrality equation for the n-type doped semiconductor is thus
\( \seteqsection {3} \) \( \seteqnumber {22} \)
\begin{equation} n = \frac {1}{2} \left ( \frac {N_\mathrm {C}}{g_\mathrm {D}} e^{\frac {E_\mathrm {D}}{k_\mathrm {B} T}} - N_\mathrm {A}^\mathrm {cp} + \sqrt { \left ( N_\mathrm {A}^\mathrm {cp} - \frac {N_\mathrm {C}}{g_\mathrm {D}} e^{\frac {E_\mathrm {D}}{k_\mathrm {B} T}} \right )^{2} + 4 \frac {N_\mathrm {C}}{g_\mathrm {D}} e^{\frac {E_\mathrm {D}}{k_\mathrm {B} T}} N_\mathrm {D} } \right ) \end{equation}
and for the p-type doped semiconductor
\( \seteqsection {3} \) \( \seteqnumber {23} \)
\begin{equation} p = \frac {1}{2} \left ( \frac {N_\mathrm {V}}{g_\mathrm {A}} e^{\frac {E_\mathrm {A}}{k_\mathrm {B} T}} - N_\mathrm {D}^\mathrm {cp} + \sqrt { \left ( N_\mathrm {D}^\mathrm {cp} - \frac {N_\mathrm {V}}{g_\mathrm {A}} e^{\frac {E_\mathrm {A}}{k_\mathrm {B} T}} \right )^{2} + 4 \frac {N_\mathrm {V}}{g_\mathrm {A}} e^{\frac {E_\mathrm {A}}{k_\mathrm {B} T}} N_\mathrm {A} } \right ). \end{equation}
In order to obtain donor (acceptor) concentrations and activation energies, the charge neutrality equation is typically fitted over the electron (hole) concentrations as a function of sample temperature.
3.1.3 Charge Neutrality Fitting
Data for fitting must be based on identical material properties (e.g., polytypes 1 and orientations) of SiC and processing techniques in order to enable a meaningful investigation of the impact of annealing on the electrical activation. Furthermore, the fabrication process parameters and techniques of the data must be identical, i.e., 1) implantation temperatures, 2) annealing ambient (commonly argon (Ar)), 3) heating method (furnace or microwave), and 4) Hall measurement technique.
The charge neutrality fits are performed to obtain the donor (ND) or the acceptor (NA) concentration. It is typically assumed that the active concentration Cact = ND for n-type and Cact = NA for p-type doping. The fitting parameters are the ionization energy (ED or EA) and the concentration of compensation (NAcp or NDcp) [135, 136]. Two donor (or acceptor) species are necessary to fit the experimental data. These species are attributed to donors (acceptors) that reside at hexagonal (h) and cubic (k) Si lattice sites. The total concentration of donors ND (acceptors NA) is given by the sum of donors (acceptors) at hexagonal and cubic lattice sites.
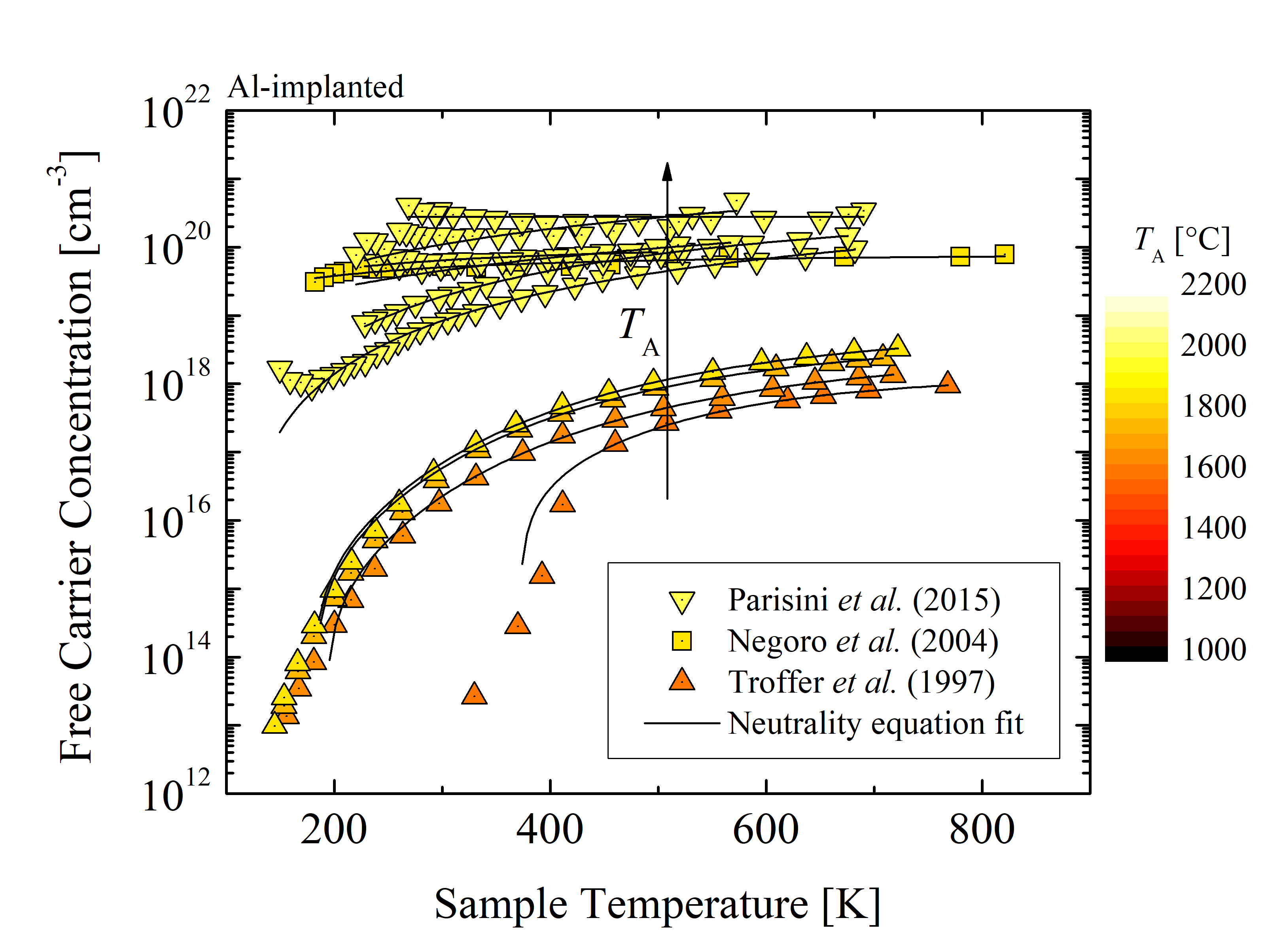
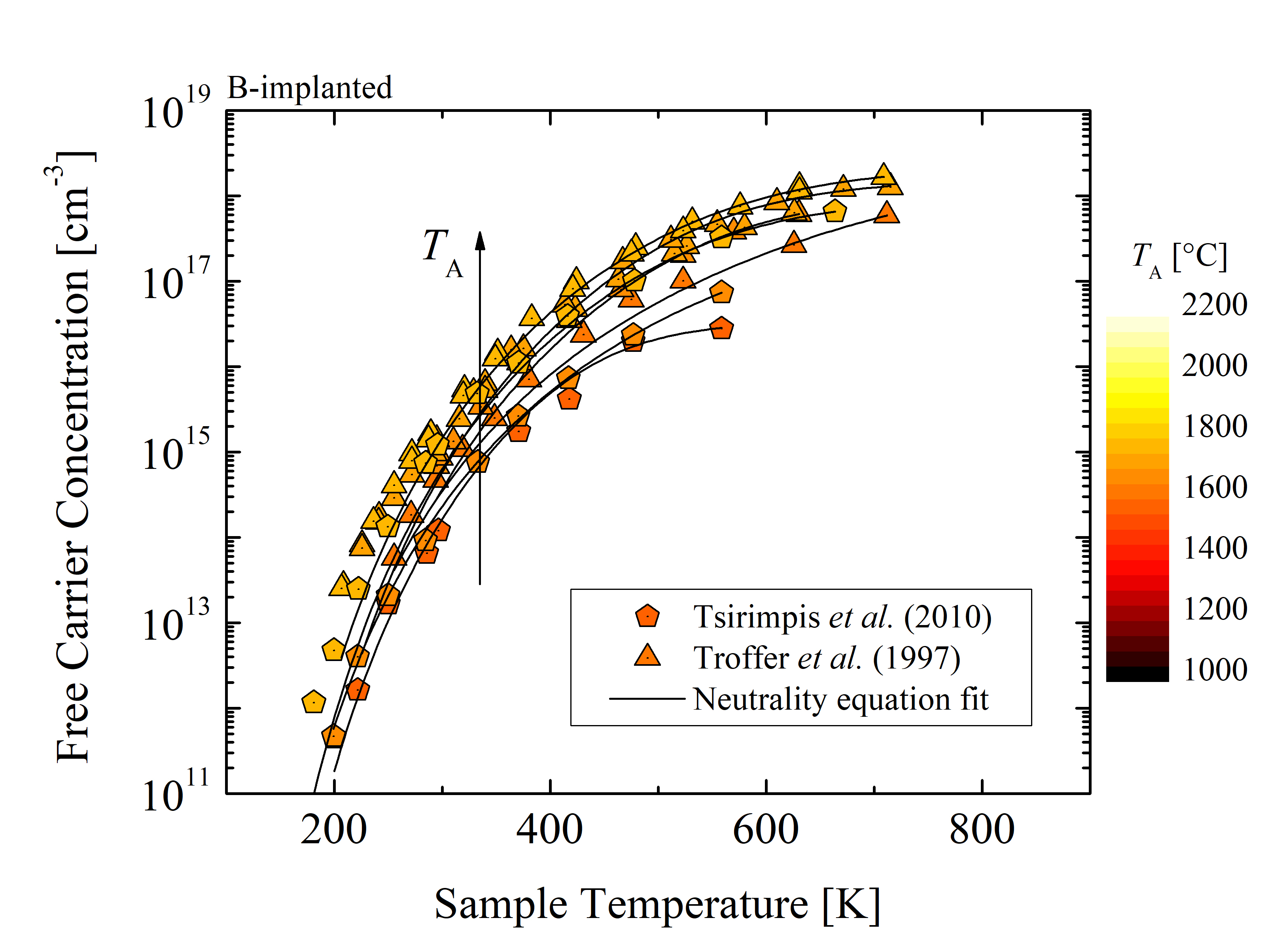
The ionization energy (ED or EA) of the implanted species is determined by the charge neutrality fitting. For P-implanted SiC the ionization energy is in average 45 meV for hexagonal and 90 meV for cubic lattice sites [137]. For N-implanted SiC the ionization energy is in average 33 meV for hexagonal and 89 meV for cubic lattice sites [138]. For Al and B-implanted SiC the total ionization energy is in the range of 191-230 meV and 285-390 meV [139]. The ionization energies are summarized in Table 3.2. The variations in ionization energies originate mostly from numerical errors due to the fitting algorithm and measurement errors due to the Hall measurement methods. The compensation concentrations are for each of the data sets different and depend on the intrinsic doping. See the provided references in Table 3.2 for a particular data set for details. The material parameters of SiC for the charge neutrality equation are described in Chapter 2, see Table 1.3.
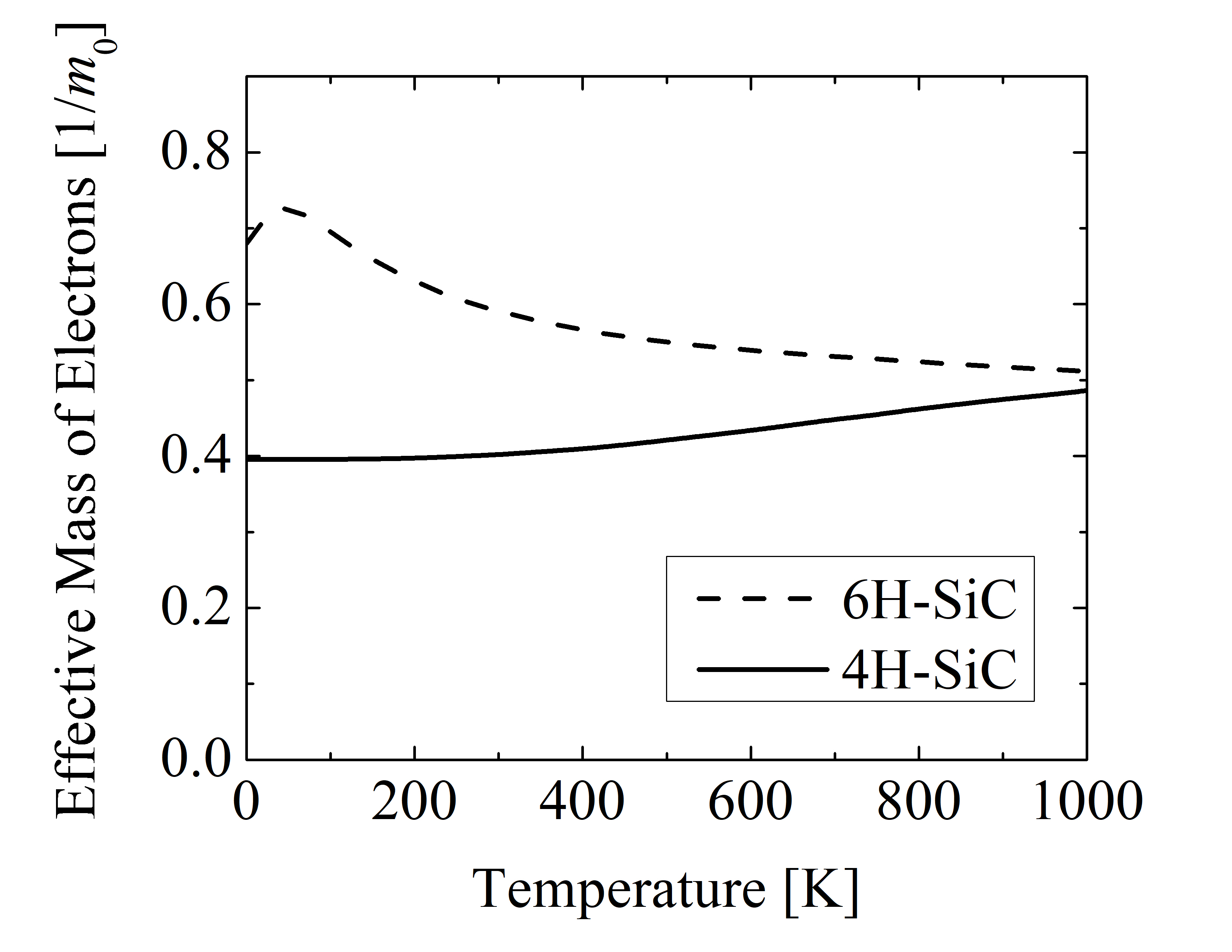
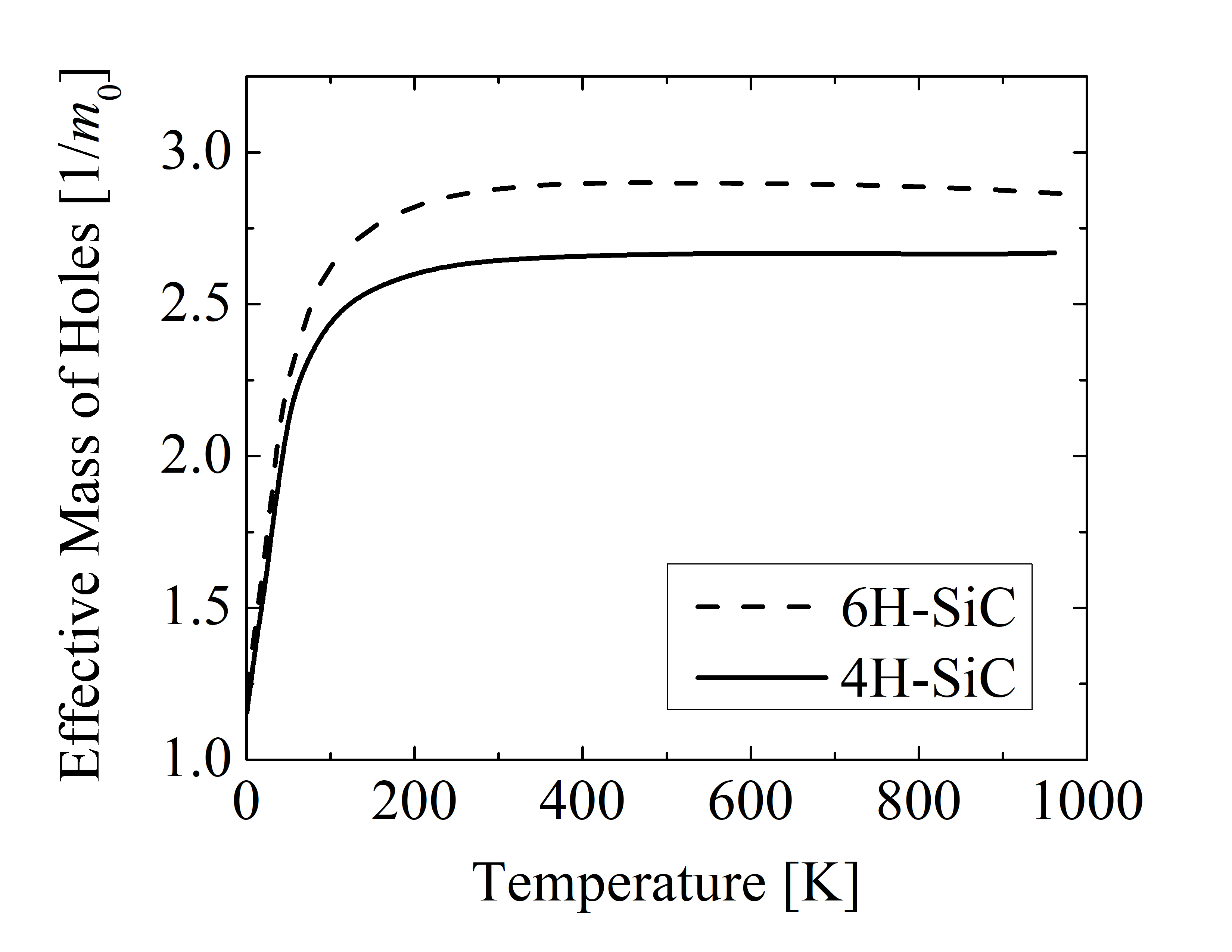
Despite the similar electrical activation ratio of 4H- and 6H-SiC, the effective mass and the number of conduction band minima differ. The number of equivalent minima in the conduction band is 3 for 4H- [140] and 6 for 6H-SiC [141]. The effective mass is in general temperature- and polytype-dependent [30]. Thus, for charge neutrality fitting the temperature-dependent effective masses of electrons and holes for 4H- and 6H-SiC are considered, shown in Figure 3.2. The effective mass of electrons for 4H-SiC is close to constant 0.4 m0 - 0.5 m0, while for 6H-SiC the effective mass varies from 0.5 m0 up to 0.8 m0. The effective mass of holes is highly temperature-dependent for T < 200 K, but for T > 200 it becomes constant. In the temperature range T < 200 K the effective mass of holes is higher for 6H-SiC (2.8 m0), compared to 4H-SiC (2.5 m0). Moreover, the degeneracy factors are different for certain SiC dopants. The value of the degeneracy factor is 2 for N [141] and 4 for P [140], Al [142], and B [143] dopants.
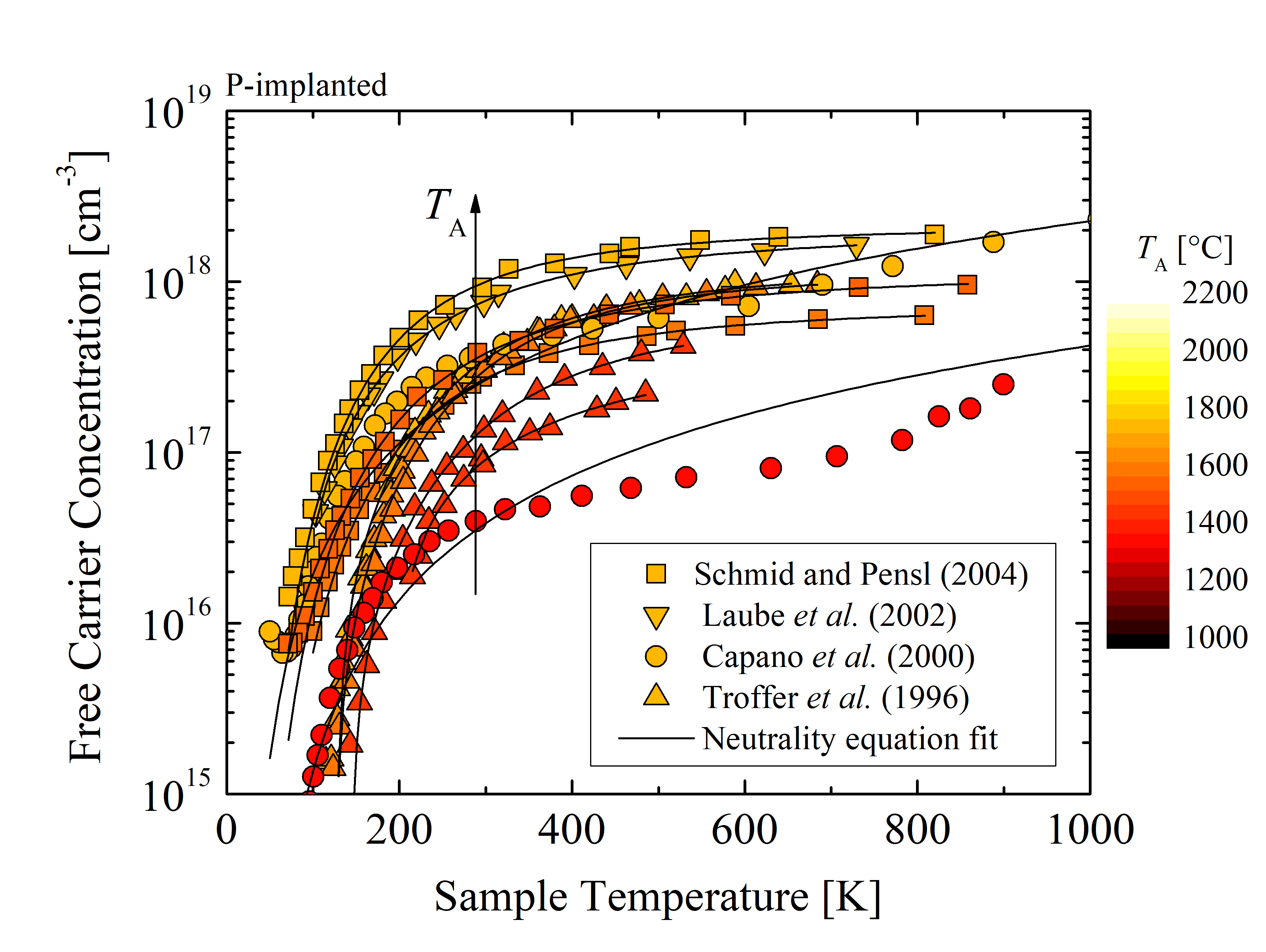
The data for the charge neutrality fitting is obtained from experimental results [140, 138, 144, 141] for P- and N-implanted (n-type) SiC and [145, 146, 147, 143] for Al- and B-implanted (p-type) SiC. The collection of these data sets for various annealing temperatures TA of the n- and p-type SiC is shown in Figures 3.3 and 3.4, respectively, where the solid lines indicate the charge neutrality fits.
Table 3.2: Ionization energies of P, N, Al, and B dopants in 4H-SiC. h and k refer to the species residing at hexagonal and cubic lattice sites, respectively.
| Dopant | Ionization Energy [meV] | Reference |
| P | 43-48 (h) | [137, 144, 140] |
| 87-95 (k) | [137, 144, 140] | |
| N | 32-34 (h) | [138, 144, 140] |
| 80-92 (k) | [138, 144, 140] | |
| Al | 191-230 (h+k) | [139, 148] |
| B | 285-390 (h+k) | [139, 143] |
1 Electrical activation between the hexagonal SiC structures, i.e., 6H- and 4H-SiC, is close to equal [134].