The electrical operation of semiconductor devices is based on the flow of mobile charges (electrons and holes) inside the device. In general, this flow of electrons and holes is a response to the external voltages applied to the device terminals. The fundamental equations describing the transport of the charge carriers are in general very complex, and their full numerical solution for modern semiconductor devices is often not feasible even when supercomputers are employed. Therefore, we conduct research on suitable models, approximations, and simplifications which retain enough accuracy at moderate numerical costs. These transport models are the foundation of TCAD codes, which shed light on many phenomena otherwise not known and unable to be studied by characterization alone. These simulation studies ultimately enable the design of consistently scaled semiconductor devices which are faster, more reliable, and more energy-efficient than their predecessors.

Classical Transport

In the semi-classical transport picture, electrons and holes are treated as point-like particles whose collective behavior is described by the seven-dimensional Boltzmann equation (BE).  Transport models of reduced complexity are derived by calculating the moments of the BE. At the lowest order, the drift-diffusion model is obtained, being the workhorse of classical device TCAD. Energy transport models and approximations of higher order account for carrier heating effects. However, modeling higher-order moments remain a numerical challenge.

Particularly for nano-scale devices, a complete solutions of the BE must be sought. Spherical harmonics expansion of the distribution function has proven to give an excellent compromise between accuracy and efficiency. In particular, full-band effects and various scattering rates (including the notorious impact ionization and carrier-carrier scattering) can be included in the description with minimal loss of accuracy. Various challenges remain and research into this area is ongoing.

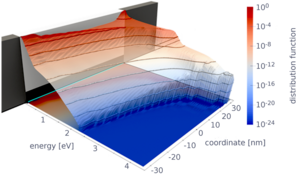
Monte Carlo solutions of the BE allow for the inclusion of very detailed physical models of the band structure and the various scattering processes. With the backward Monte Carlo method the time for computing the device characteristics is drastically reduced. Current research addresses novel algorithms that deal with the nonlinearity of the scattering operator in the case of carrier-carrier scattering and with variance reduction techniques.

Quantum Transport

Effects originating from the quantum mechanical nature of carriers play an important role in nanoelectronic devices and require appropriate modeling. The non-equilibrium Green’s function (NEGF) method has become the de facto standard for device simulation at the nanoscale. It owes this prominence to both its entirely quantum mechanical formulation of carrier transport and its expandability to a variety of interaction effects such as carrier scattering with phonons and defects, interaction with radiation, or spin polarization. Carrier tunneling, quantum confinement, and Fermi-Dirac statistics are intrinsically included. This high level of physical modeling accuracy, however, comes at the expense of high computational cost. Research is focusing on the development of efficient algorithms for dissipative quantum transport, parallel algorithms, and high-performance computing methods.  For TCAD applications, numerical solutions of the NEGF equations on an unstructured mesh are required.

The Wigner formalism extends many classical concepts and provides a phase space formulation of quantum mechanics. A transport equation which combines the coherent Wigner equation with the Boltzmann scattering operator describes the decoherence effects caused by the environment.  This equation bridges the gap between full quantum transport and classical transport.

Current activities include the development of a magnetic field aware Wigner model. The theory relies on the Weyl-Stratonovich transform for obtaining an invariant formulation under a general electromagnetic gauge. We apply the Wigner model to novel quantum processes, in particular for the emerging area of entangletronics.  Entangletronics unifies methods and principles for electron state control and engineering, aiming to create quantum states with given desired properties. Development of ViennaWD, in particular the Wigner Ensemble Monte Carlo simulation code based on a signed particle approach is ongoing.