



Next: List of Tables
Up: Dissertation T. Windbacher
Previous: Constants
- 2.1. Scheme of a high-k gate stack. By exchanging the
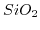 gate-dielectric with
gate-dielectric with 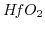 the critical oxide thickness of
the critical oxide thickness of
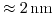 for tunneling can be met while keeping control over the channel.
for tunneling can be met while keeping control over the channel.
- 2.2. Basic scheme of a flash memory cell. Depending on the charge stored in the floating gate one bit SLC or multiple bits MLC can be saved.
- 2.3. Schemes of the basic circuits for NAND and NOR flash memory devices.
- 2.4. Scheme of a SONOS gate stack.
- 2.5. Overview of common strain techniques.
- 2.6. Scheme for different global strain techniques: 1.) strained silicon layer on
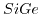 on bulk wafer; 2.) strained silicon layer directly on insulator (SDGOI); 3.) strained silicon layer on
on bulk wafer; 2.) strained silicon layer directly on insulator (SDGOI); 3.) strained silicon layer on 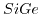 substrate on insulator (SSGOI).
substrate on insulator (SSGOI).
- 2.7. Combining selective epitaxial growth in source and drain regions and a stress liner to introduce tensile uniaxial stress for n-channel MOSFETs and compressive uniaxial stress for p-channel MOSFETs.
- 2.8. Schematic views for the different FeFET designs.
- 2.9. The working principal of a BioFET. If charged, sample molecules attach to the receptors at the biofunctionalized surface and the potential within the semiconductor changes. This causes a change in the resistance of the field-effect transistors channel.
- 3.1. Scheme of stress components and how they act on an infinitesimal cube.
- 3.2. Energy dispersion of the conduction bands
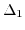 and
and
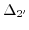 near the zone boundary
near the zone boundary  point along
point along
![$ \left [001\right ]$](img8.png) . For
. For
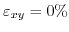 the conduction bands are degenerate at the zone boundary. Introduction of shear strain
the conduction bands are degenerate at the zone boundary. Introduction of shear strain
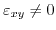 lifts this degeneracy and opens up a gap. The energy separation
lifts this degeneracy and opens up a gap. The energy separation
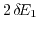 between the bands becomes larger with increasing strain
between the bands becomes larger with increasing strain
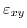 . At the same time the two minima of the lower conduction band
. At the same time the two minima of the lower conduction band
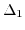 move closer to the zone boundary with rising strain
move closer to the zone boundary with rising strain
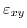 , until they merge at the zone boundary and stay there for further increasing strain.
, until they merge at the zone boundary and stay there for further increasing strain.
- 3.3. Energy dispersion of the two lowest conduction bands at the zone boundaries
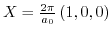 and
and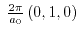 . The band separation of unstrained
. The band separation of unstrained 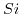 at the conduction band edge
at the conduction band edge
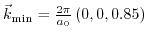 is denoted by
is denoted by 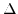 . Contrary to the conduction bands along
. Contrary to the conduction bands along
![$ \left [001\right ]$](img8.png) the conduction bands along
the conduction bands along
![$ \left [100\right ]$](img18.png) and
and
![$ \left [010\right ]$](img19.png) are not affected by shear strain
are not affected by shear strain
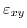 .
.
- 4.1. Potential in an ultra-thin SOI film of a single-gate MOSFET (left) and a corresponding model square well potential with infinite walls.
- 4.2. Conduction band profile close to the X-point for
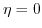 (solid lines,
(solid lines, 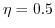 (dashed lines), and
(dashed lines), and 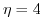 (dashed-dotted line).
(dashed-dotted line).
- 4.3. The right hand side of (4.16) and (4.17) plotted close to the point
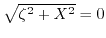 . It is clearly seen that the sign of the square root must be alternated at this point.
. It is clearly seen that the sign of the square root must be alternated at this point.
- 4.4. Subband quantization energies
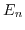 (normalized to the ground subband energy) for a film thickness of
(normalized to the ground subband energy) for a film thickness of
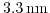 . The valley splitting appears for non-zero shear strain
. The valley splitting appears for non-zero shear strain 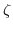 .
.
- 4.5. The same as in Fig. 4.4 for a film thickness
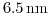 . The valley splitting depends strongly on the film thickness. The valley splitting is maximal at high strain values.
. The valley splitting depends strongly on the film thickness. The valley splitting is maximal at high strain values.
- 4.6. Difference of the subband quantization energies
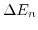 (normalized to the ground subband energy) from (4.18) and (4.19) for a film thickness of
(normalized to the ground subband energy) from (4.18) and (4.19) for a film thickness of
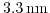 . The valley splitting appears for non-zero shear strain
. The valley splitting appears for non-zero shear strain 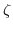 .
.
- 4.7.
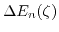 for a film thickness of
for a film thickness of
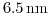 . The splitting depends strongly on the film thickness.
. The splitting depends strongly on the film thickness.
- 4.8. Splitting induced by shear strain for several film thicknesses. As can be seen for ultra-thin films the splitting is already larger than
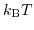 for moderate stress levels.
for moderate stress levels.
- 4.9. Ultra-thin films exhibit different effective masses for the two ground subbands even without stress. The thinner the film the more pronunced is the difference in effective masses.
- 4.10. The dependence of the effective masses on the film thickness for the lowest two subbands.
- 4.11. The two ground subbands as contour plots.
- 5.1. Most biological and chemical experiments are carried out in an ionic solution. Polar solutions (like water) can break up strong ionic bonds and ease chemical reactions. Each ion (red and dark blue) is surrounded by an aggregate of water molecules. The non-vanishing dipole moment of the water molecules weakens the electric field binding the ions together.
- 5.2. The different surface effects. The (non-) specific adsorbtion, due to (partial) release of the solvation shell and conjoint closer approach to the interface, the so called IHP, is depicted with blue circles. The effect of surface complexation, due to the high affinity of attracting counter ions, is shown by the green circle. The Stern layer ends at the OHP, the zone without counter ions exhibiting their full water shell (depicted with red circles, surrounded by small light blue circles), and is continued by the Gouy-Chapman layer.
- 5.3. The insulator surface exhibits open binding sites due to the lack of insulator bonding partners at the surface. These binding sites can be either negatively/positively charged or neutral, depending on the properties of the liquid covering the surface. The surface charge density depends on the surface potential
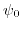 , material properties, and the local hydrogen concentration
, material properties, and the local hydrogen concentration
![$ \left [\mathrm {H}^{+}\right ]_{b}$](img33.png) .
.
- 5.4. As illustrated in the panels a.) to d.), the higher the surface site density
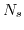 is the bigger the maximal surface charge density
is the bigger the maximal surface charge density
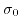 will be. All curves show two distinct steps in the relation between surface charge density
will be. All curves show two distinct steps in the relation between surface charge density
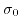 and surface potential
and surface potential 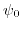 . The larger the difference between the forward positively charging reaction rate
. The larger the difference between the forward positively charging reaction rate 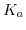 and the negatively charging reaction rate
and the negatively charging reaction rate 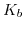 the more pronounced and steeper are these steps.
the more pronounced and steeper are these steps.
- 5.5. Potential profile in an ISFET structure for a cut along the z-axis.
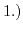 The potential drop at the electrode-electrolyte interface, caused by the Gouy-Chapman-Stern double layer (
The potential drop at the electrode-electrolyte interface, caused by the Gouy-Chapman-Stern double layer (
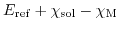 ).
).
 The Gouy-Chapman-Stern double layer at the electrolyte-insulator
The Gouy-Chapman-Stern double layer at the electrolyte-insulator
interface (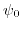 ).
).
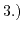 The potential drop in the insulator (
The potential drop in the insulator (
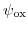 ).
).
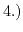 The potential drop due to the depletion charges in the semiconductor (
The potential drop due to the depletion charges in the semiconductor (
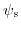 ).
).
- 5.6. Introducing a membrane into the ISFET hinders unwanted ion-species to diffuse to the insulator interface. Thus, only the selected ion species can approach the gate insulator, and the selectivity of the ISFET is ensured.
- 5.7. Potential profile for a cut perpendicular to the surface of the ISFET (beginning at the left border: semiconductor, dielectric, and solute). The simulations were carried out for a.)
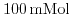 , b.)
, b.)
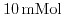 , and c.)
, and c.)
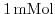 phosphate buffered saline (PBS).
phosphate buffered saline (PBS).
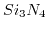 was utilized as gate dielectric at different pH values. Simulation results with the parameter set by Harame et al.[1], fit excellent the experimental values. With decreasing buffer concentration the screening is reduced and the saturation starts at higher pH values. The reduced screening is also reflected in the prolonged decay of the potential in the liquid.
was utilized as gate dielectric at different pH values. Simulation results with the parameter set by Harame et al.[1], fit excellent the experimental values. With decreasing buffer concentration the screening is reduced and the saturation starts at higher pH values. The reduced screening is also reflected in the prolonged decay of the potential in the liquid.
- 6.1. Sensing a macromolecule via the long-range field-effect.
- 6.2. BioFET: different simulation zones.
- 6.3. The dependence of the Debye length on ion concentration for a
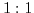 electrolytic solution. Higher salt concentration reduces the repulsion between complementary DNA strands, and thus accelerates the hybridization events, but, at the same time, decreases the Debye length
electrolytic solution. Higher salt concentration reduces the repulsion between complementary DNA strands, and thus accelerates the hybridization events, but, at the same time, decreases the Debye length
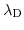 and therefore the device signal.
and therefore the device signal.
- 6.4. The dependence of the concentrations for different ionic components and the ionic strength on the local pH.
- 6.5. Illustrating the different screening characteristica for the Poisson-Boltzmann, the extended Poisson-Boltzmann, and the Debye-Hückel model. In the limit of
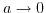 the extended Poisson-Boltzmann model rejoins the Poisson-Boltzmann model, while for increasing closest possible ion distance
the extended Poisson-Boltzmann model rejoins the Poisson-Boltzmann model, while for increasing closest possible ion distance 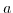 , which corresponds to a decreasing salt concentration, the screening is reduced and resembles for
, which corresponds to a decreasing salt concentration, the screening is reduced and resembles for 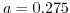 the Debye-Hückel model.
the Debye-Hückel model.
- 6.6. a.)The unbound single-stranded DNA at the surface of the dielectric.
b.)Single-stranded DNA on the oxide surface. Two iso-surfaces for plus and minus
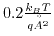 are shown.
are shown.
- 6.7. a.)Potential profile in the whole device for double-stranded DNA perpendicular to surface.
b.)Potential profile at the interface (from left to right: semiconductor, oxide, solute).
- 6.8. a.)Output characteristics before hybridization for a mean distance
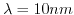 and
and
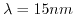 without dipole moment.
without dipole moment.
b.)Output characteristics after hybridization for a mean distance
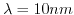 and
and
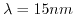 without dipole moment.
without dipole moment.
- 6.9. a.)Output characteristics after hybridization for a mean distance
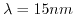 : without dipole moment, with
: without dipole moment, with 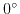 , and
, and
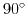 .
.
b.)Potential profile from semiconductor to oxide (left to right).
- 6.10. a.)Transfer characteristics of a SGFET for Poisson-Boltzmann model and DNA charge modeled via space charge density.
b.)Transfer characteristics of a SGFET for Poisson-Boltzmann model and DNA charge modeled via sheet charge density.
c.)Transfer characteristics of a SGFET for Debye-Hückel model and DNA charge modeled via space charge density.
- 6.11. Potential for the Poisson-Boltzmann model with space charge, starting from the semiconductor (left) and ending in the analyte (right). It can be seen that doubling the charge does not lead to twice the potential shift due to nonlinear screening.
- 6.12. Potential for the Poisson-Boltzmann model with sheet charge, starting from the semiconductor (left) and ending in the analyte (right). Here the shift is a bit increased but far away from the values from the measurement. However, also here doubling the charge does not lead to twice the potential shift due to nonlinear screening.
- 6.13. Potential for the Debye-Hückel model with space charge, starting from the semiconductor (left) and ending in the analyte (right). It can be seen that doubling the charge leads to twice the potential shift due to the weaker linear screening.
- 6.14. Scheme of the tetrameric protein streptavidin and biotin.
- 6.15. Biotin-streptavidin complex [2] on the oxide surface. Two iso-surfaces for plus and minus
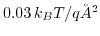 are shown.
are shown.
- 6.16. Output curve for
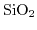 for unprepared, prepared but unbound, and bound state at
for unprepared, prepared but unbound, and bound state at
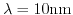 and
and
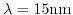 , respectively.
, respectively.
- 6.17. Output curve for
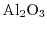 for unprepared, prepared but unbound, and bound state at
for unprepared, prepared but unbound, and bound state at
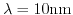 and
and
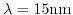 , respectively.
, respectively.
- 6.18. Output curve for
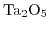 for unprepared, prepared but unbound, and bound state at
for unprepared, prepared but unbound, and bound state at
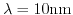 and
and
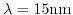 , respectively.
, respectively.
- 6.19. Output curves for
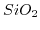 ,
,
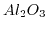 , and
, and
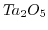 for calculation without dipole moment,
for calculation without dipole moment, 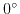 (perpendicular to surface), and
(perpendicular to surface), and
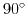 (parallel to surface).
(parallel to surface).
- 6.20. Small signal resistance for
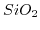 ,
,
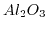 , and
, and
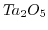 for calculation without dipole moment,
for calculation without dipole moment, 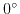 (perpendicular to surface), and
(perpendicular to surface), and
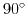 (parallel to surface) at biotin only.
(parallel to surface) at biotin only.
- 6.21. Small signal resistance for
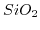 ,
,
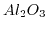 , and
, and
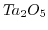 for calculation without dipole moment,
for calculation without dipole moment, 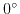 (perpendicular to surface), and
(perpendicular to surface), and
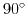 (parallel to surface) at bound state (biotin-streptavidin).
(parallel to surface) at bound state (biotin-streptavidin).




Next: List of Tables
Up: Dissertation T. Windbacher
Previous: Constants
T. Windbacher: Engineering Gate Stacks for Field-Effect Transistors