Charge Trapping and Variability in CMOS Technologiesat Cryogenic Temperatures

7.3 Random Telegraph Noise

On small area devices single charge capture and emission events are observed in the measured drain-source current or the corresponding (math image) curve as discrete steps. Every defect can therefore be identified by $\{\eta , \tauc ,\taue \}$ , where $\eta$ is the mean step height (either in the current or the equivalent representation) and and are the mean capture and emission times, respectively. This set of parameters can be found for various gate voltage and temperature conditions $\{\eta , \tauc ,\taue \}(\vg ,T)$ . It has to be noted that the step heights and the charge transition times are stochastic quantities. The step height is normally distributed around a mean value. 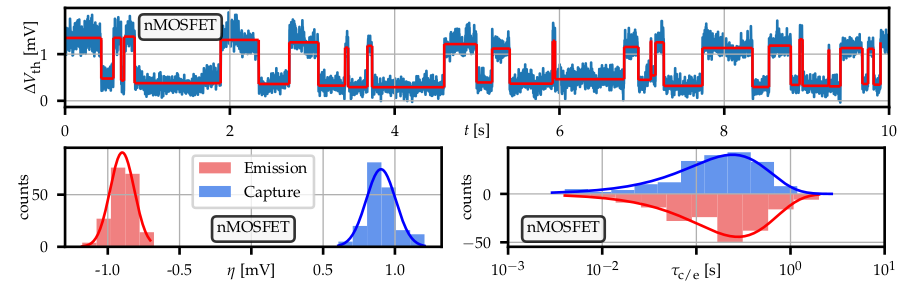As the charge transition times can be described as a Markov process, it can be shown using the Master equation that capture and emission times are exponentially distributed [174], as can be seen for the exemplary trace in Fig. 7.3.

For the extraction of the distributions of step heights, time constants and the corresponding set of mean parameters $\{\eta , \tauc ,\taue \}$ which identifies a defect, a precise detection of the position of the discrete steps is crucial. Since there should be ideally tens or hundreds of discrete steps in a single RTN trace, and typically multiple traces for different temperatures and gate voltage conditions are needed, an automatic or semi-automatic detection algorithm of the position and heights of the steps is required. In this work, two different algorithms were used: the Canny edge detector and Otsu’s method which will be presented in the following sections.

7.3.1 Canny Edge Detector

The Canny edge detector was developed by John F. Canny in 1986 and was initially designed to detect edges in images [235]. While the original algorithm was developed for 2-dimensional applications, the step detection in RTN signals is a 1-dimensional problem which simplifies the algorithm considerably. Analogous to the deviation in [140], the algorithm can be broken down into the following steps, shown in Fig. 7.4:

1. The intensity of the measured RTN signal $S$ increases when convoluting it with a discretized first derivative of a Gaussian filter $G$

$(7.9) \{begin}{align} R[n] = (S*G)[n]\sum \limits _{k=-W}^W S[k]G’[n-k], \{end}{align}$

where $W$ is the width of the truncation and

$(7.10) \{begin}{align} G’[t] = -\frac {t}{\sqrt {2\pi }\sigma ^3}\mathrm {e}^{-\frac {t^2}{2\sigma ^2}} \{end}{align}$

with $\sigma$ being the width of the Gaussian filter.
2. The convuluted signal $R[n]$ can be simplified by applying a non-maximum suppression

$(7.11) \{begin}{align} R_\mathrm {m}[n] = \left \{\begin {array}{ll} R[n], & (|R[n]|>R[n+1] \wedge |R[n]|>R[n-1]) \\ 0, & \mathrm {else}\end {array}\right . . \{end}{align}$
3. A threshold value $R_\mathrm {th}$ is chosen, which suppresses responses from noise:

$(7.12) \{begin}{align} R_\mathrm {t}[n] = \left \{\begin {array}{ll} R[n], & (|R_m[n]|>R_\mathrm {th}) \\ 0, & \mathrm {else}\end {array}\right . . \{end}{align}$

The sign of $R_\mathrm {t}[n]$ determines whether an upwards or downwards step is detected, and the height of the step can be extracted from the original signal. This algorithm has a low error rate and the localization of the edges is very precise. If there are two active defects in a single signal, the detected steps can be clustered by their step heights using for example a K-means algorithm [236]. However, the algorithm has the disadvantage that the width of the Gaussian filter $\sigma$ and the threshold value $R_\mathrm {th}$ are input parameters which have be to varied to detect different active defects. Thus the detection quality depends on the selected parameters. However, when dealing with a large set of RTN signals, a fully automated algorithm for step detection is necessary, like for example Otsu’s method which is presented in the next section.

7.3.2 Otsu’s Method

Otsu’s method is an algorithm for automatic thresholding and was developed by Nobuyuki Otsu in 1979 [237]. Just like the Canny edge detector, Otsu’s method was initially designed for image thresholding, thus for separating pixels into two classes: foreground and background. The algorithm searches for a threshold value which maximizes the inter-class variance of the two classes $0$ and $1$ equivalent to minimizing the inter-class variance. This process is performed in four steps:

1. The normalized histogram and the probability $p(i)$ for every bin $i$ of $L$ bins in total is computed. The normalized histogram for the signal in Fig. 7.5 (left) can be seen in Fig. 7.5 (right).
2. The class probabilities $\omega _{0,1}(t=0)$ and class means $\mu _{0,1}(t=0)$ are initialized for $t=0$ .
3. Next, the algorithm steps through all thresholds $t=1,\dots ,L-1$ and computes the class probabilities $\omega _{0,1}(t)$ , the class means $\mu _{0,1}(t)$ and the inter-class variances $\sigma _b^2(t)$ . Here, the class probabilities are defined as

$(7.13) \{begin}{align} \begin {split} \omega _0(t)&=\sum \limits _{i=0}^{t-1} p(i)~\mathrm {and}\\ \omega _1(t)&=\sum \limits _{i=t}^{L-1} p(i). \end {split} \{end}{align}$

Using the class probabilities, the class means $\mu _{0,1}(t)$ are obtain as

$(7.14) \{begin}{align} \begin {split} \mu _0(t)=\frac {1}{\omega _0(t)}\sum \limits _{i=0}^{t-1}ip(i)\\ \mu _1(t)=\frac {1}{\omega _1(t)}\sum \limits _{i=t}^{L-1}ip(i) \end {split} \{end}{align}$

which allows to compute the inter-class variance

$(7.15) \{begin}{align} \sigma _b^2(t) = \omega _0(t)\omega _1(t)[\mu _0(t)-\mu _1(t)]^2. \{end}{align}$

In Fig. 7.5 (right) the inter-class variance is plotted for every threshold value.
4. Finally, the optimum threshold value is determined as the threshold $t$ for which the respective inter-class variance is maximized.

After obtaining the threshold $t$ with Otsu’s method, a step in the signal $S$ at timestep $i$ is given at those points, where

$(7.16) \{begin}{align} \Big (S(i-1)<t \land S(i)>t\Big ) \lor \Big (S(i-1)>t \land S(i)<t\Big ) \{end}{align}$

holds.

Compared to the Canny edge detector, Otsu’s method has the advantage that the thresholding is completely automated. In general, it can be beneficial to apply a filter before the automated thresholding to suppress measurement noise. While this has the disadvantage that very short time constants get lost, it renders the thresholding extremely robust and even allows the detection of small step heights. In this work, the denoising algorithm proposed by Chambolle was used [238].

Otsu’s method can only be applied on measurement data including a single active defect. In case of the detection of multiple active defects (multi-level RTN) typically only the most prominent defect signal will be extracted. To avoid incorrect detection additional sanity checks are applied, e.g. a Kolmogorov-Smirnov test for testing if capture and emission times follow an exponential distribution. For a detailed analysis of multi-level RTN more advanced techniques as a factorial hidden Markov model analysis are needed [239].