Phenomenological Single-Particle
Modeling of Reactive Transport
in Semiconductor Processing

5.3 Reactor Loading Effect

As already seen in Tab. 5.2, there appears to be a reduction in the \(\mathit {PWR}_{\mathrm {Si}}\) for the second etch step. This is a strong indication of the presence of the reactor loading effect, that is, a reduction in the etch rate due to an increase in the exposed wafer surface [46, 131]. With more exposed Si, which is the case for the second etch step after photoresist removal, the same number of reactants are spread across a larger area, leading to lower etch rates. This effect is different from AR dependence due to Knudsen transport, discussed in Section 3.6.1, since it does not depend on characteristics of the etched feature. The reactor loading effect, often just named "loading effect", is also distinct from microloading [184] which is a variation on etch rates due to the local density of features, even if the total exposed area is equal.

In principle, reactor loading can be modeled if the total exposed wafer area is known [46]. However, this information is not always accessible, and, additionally, such models still require fitting coefficients. Instead, the approach taken is to treat the PWRs, thus the loading effect, as a model parameter not only for each reactor condition but also for each photoresist or hardmask configuration. At the core of this approach is the approximation that the exposed area is constant during the etch step which is valid for low photoresist or hardmask etch rates.

This effect has been experimentally investigated by Panduranga et al. [171]. In their work, they attempt to deliberately construct a regime with lower etch rates by placing the individual chips over a larger and unmasked silicon carrier wafer.
They investigate two distinct situations: A low loading regime, by placing the chips directly over the stainless steel carrier plate, and a high loading regime with chips on the silicon carrier wafer. To quantify the etch depth, the chips are initially patterned with a hardmask (chromium-on-oxide) containing cylindrical holes with \(d=\SI {500}{\micro \meter }\). Then, the etching proceeds on an ICP reactor with the conditions reported in Tab. 5.1. The final shape of the surface is measured with a mechanical profilometer.

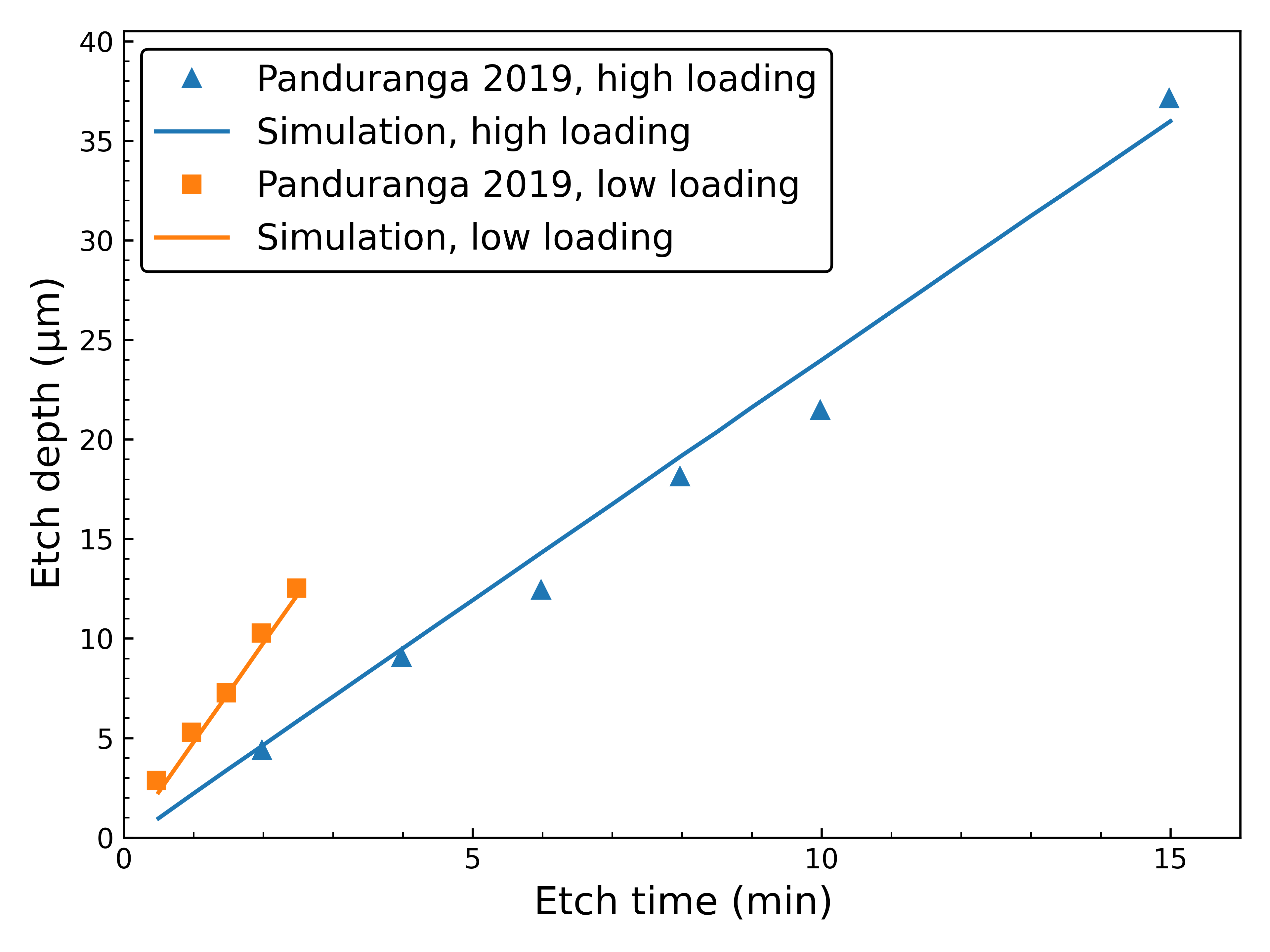
The original authors assume that there are no limitations due to visibility, thus they calculate the PWRs from the etch depths at the center. However, since visibility effects often play a subtle role, the simulation considers the entire geometry. The \(\mathit {PWR}_{\mathrm {Si}}\) is manually adjusted for each of the reported regimes to encounter the best fit to the reported experimental depths. The resulting parameters are disclosed in Tab. 5.4 and the time evolution of the etch depth at the center of the cylindrical opening is shown in Fig. 5.3. The good agreement is evidence that the approach of modeling the loading effect through treating the PWR as a fitting parameter is valid. In comparison to the original work, the values are within the range of reported etch rates for the high loading regime (between \(2.07\) and \(\SI {2.47}{\micro \meter \per \minute }\)).

.
Low loading \(\mathit {PWR}_{\mathrm {Si}}\)	High loading \(\mathit {PWR}_{\mathrm {Si}}\)
\(\SI {4.92}{\micro \meter \per \minute }\)	\(\SI {2.40}{\micro \meter \per \minute }\)

Table 5.4: Plane-wafer etch rates for the low and high reactor loading regimes calibrated to experimental etch depths reported in [171].

Phenomenological Single-Particle Modeling of Reactive Transport in Semiconductor Processing

5.3 Reactor Loading Effect

Phenomenological Single-Particle
Modeling of Reactive Transport
in Semiconductor Processing