


Next: List of Tables
Up: Dissertation Otmar Ertl
Previous: Contents
- 2.1. The particle transport is broken up by describing the transport to
 on reactor-scale and the transport from
on reactor-scale and the transport from
 to
to
 on feature-scale.
on feature-scale.
- 3.1. A problematic case which may occur and which needs special consideration. For the update of the neighboring pair of active grid points (black) with LS values
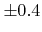 opposite signed surface velocities (arrows) are used. This leads to a neighboring pair of non-active grid points with opposite signed LS values.
opposite signed surface velocities (arrows) are used. This leads to a neighboring pair of non-active grid points with opposite signed LS values.
- 3.2. Two examples, where the sparse field method produces inefficient
sets of active (black) grid points. The surface
 moves with a uniform positive surface velocity (arrows). After a time step some active grid points (squares) do not have a neighbor with opposite signed LS value.
moves with a uniform positive surface velocity (arrows). After a time step some active grid points (squares) do not have a neighbor with opposite signed LS value.
- 3.3. A LS function representing a triangle is resolved on a
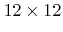 grid. Only the LS of defined grid points (green) must be stored. Memory can be saved by not storing the LS values of all other positive (blue) and negative (red) undefined grid points. The LS values of all defined grid points are given on the right-hand side.
grid. Only the LS of defined grid points (green) must be stored. Memory can be saved by not storing the LS values of all other positive (blue) and negative (red) undefined grid points. The LS values of all defined grid points are given on the right-hand side.
- 3.4. The RLE data structure for the example given in Figure 3.3. For each of the 12 grid lines along the
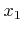 -direction an index is stored in the start indices array to the corresponding run type sequence. Three different types of run codes can be distinguished: Undefined runs which are either positive (blue) or negative (red), and defined runs (green) whose run codes give the corresponding start indices in the LS values array. Another array stores the run breaks from which the start and end indices of a run can be obtained. The size of the run breaks array is always equal to the difference of the sizes of the run types array and the start indices array.
-direction an index is stored in the start indices array to the corresponding run type sequence. Three different types of run codes can be distinguished: Undefined runs which are either positive (blue) or negative (red), and defined runs (green) whose run codes give the corresponding start indices in the LS values array. Another array stores the run breaks from which the start and end indices of a run can be obtained. The size of the run breaks array is always equal to the difference of the sizes of the run types array and the start indices array.
- 3.5. The defined grid points and their associated LS values of the example shown in Figure 3.3 as stored in a DTG. The hierarchical structure is obtained by subsequent projection of grid points to a lower dimension, and combining connected sequences of indices along a grid line. The minimum and maximum indices of such a sequence are stored together with an array index which provides access to its members. Since the topmost array always contains just a single entry with value 0, it can be omitted. This array is not included in the original definition of the DTG and is only shown to emphasize the hierarchical structure.
- 3.6. The H-RLE data structure applies run-length encoding hierarchically over all grid dimensions in order to obtain an efficient LS data structure which combines the advantages of run-length encoding and the hierarchically organized DTG.
- 3.7. The segmentation of the grid (black thick lines) which is implicitly defined by the H-RLE data structure. Each segment represents either a run of positive (blue) or negative (red) undefined grid points or a single defined grid point (green).
- 4.1. The orientation of the normal vector
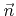 on a line segment and on a triangle as defined in this work with respect to the order of nodes
on a line segment and on a triangle as defined in this work with respect to the order of nodes
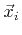 .
.
- 4.2. (a) Two segments of the surface mesh (gray) meet on a grid line (black). Hence, for both grid points the distance is equal to both segments. As consequence the determination of the signed distance according to (4.4) is ambiguous. (b) The distance transform can produce inefficient sets of active grid points. The bottom left grid point does not have an opposite signed neighbor.
- 4.3. (a) A surface embedded in a domain with extensions
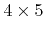 . However, due to the different boundary conditions in
. However, due to the different boundary conditions in 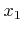 -direction (reflective) and
-direction (reflective) and 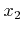 -direction (periodic)
-direction (periodic) 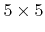 grid points are used for the discretization of the level set function. (b) Basic iterators traverse the segments of the H-RLE data structure according to their numbering. (c) The segmentation as seen by an iterator with offset
grid points are used for the discretization of the level set function. (b) Basic iterators traverse the segments of the H-RLE data structure according to their numbering. (c) The segmentation as seen by an iterator with offset
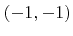 . (d) The same for an iterator with offset
. (d) The same for an iterator with offset
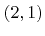 .
.
- 4.4. Boolean operations can be calculated using level sets. The union of a cuboid (a) and a cone (b) subtracted by a sphere (c) is the structure shown in (d).
- 4.5. After an isotropic deposition process the structure is exposed to CMP. This process is realized using Boolean operations applied on the LS representations of the initial surface (blue) and the surface after the deposition (yellow).
- 4.6. Boolean operations using level sets can be applied to describe pattern transfer.
- 4.7. The final surface after a smoothing operation is applied to the geometry given in Figure 4.5a. The curvature is limited by
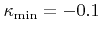 and
and
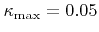 .
.
- 4.8. (a) A geometry consisting of 3 different materials, where
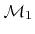 represents the substrate,
represents the substrate,
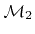 the mask, and
the mask, and
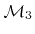 a passivation layer. (b) Description of the structure using 3 enclosing LSs. (c) Alternative representation where one LS describes the common surface and two others the interfaces between the different material regions.
a passivation layer. (b) Description of the structure using 3 enclosing LSs. (c) Alternative representation where one LS describes the common surface and two others the interfaces between the different material regions.
- 4.9. Renumbering of material regions (a) leads to a different LS representation (b).
- 4.10. A test structure with lateral extensions
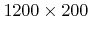 and three layers on top of the substrate (red). The first layer cannot be clearly seen, since it has a thickness of only 0.5. The second layer (blue) and the mask (green) both have a thickness of 50.
and three layers on top of the substrate (red). The first layer cannot be clearly seen, since it has a thickness of only 0.5. The second layer (blue) and the mask (green) both have a thickness of 50.
- 4.11. The multi-LS representation of the initial geometry. Four LS functions are used to describe the four different material regions.
- 4.12. The final geometry after isotropic etching with material-dependent etch rates. The etch rate was 0.1 grid spacings per time step for the mask, and 0.025 for the very thin layer. For the other two material regions the etch rate was set to 1.
- 4.13. A surface
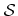 and its H-RLE representation are shown. In this example, the LS values are only defined for the active grid points. Positive (blue) and negative (red) runs of undefined grid points are assumed to have LS values
and its H-RLE representation are shown. In this example, the LS values are only defined for the active grid points. Positive (blue) and negative (red) runs of undefined grid points are assumed to have LS values 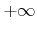 and
and 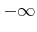 , respectively. The dark green grid points do not fulfill the visibility criterion.
, respectively. The dark green grid points do not fulfill the visibility criterion.
- 4.14. The structure given in Figure 4.12 after processing with a directional material-dependent etch process.
- 4.15. A schematic illustration of the Bosch process. The deposition of a passivation layer protects the sidewalls during the subsequent etching cycle.
- 4.16. The simulation of a Bosch process. The corresponding LS representation is shown for different times. The corresponding number of applied deposition and etching cycles can be retrieved from the subfigure captions.
- 4.17. (a) The surface
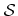 of a geometry with a void. Blue and red points have positive and negative LS values, respectively. Defined grid points are also colored green. (b) The corresponding segments of the H-RLE data structure. Their numbers give the vertex of the reduced graph they are assigned to. (c) The reduced graph which is set up to find the connected components.
of a geometry with a void. Blue and red points have positive and negative LS values, respectively. Defined grid points are also colored green. (b) The corresponding segments of the H-RLE data structure. Their numbers give the vertex of the reduced graph they are assigned to. (c) The reduced graph which is set up to find the connected components.
- 4.18. Isotropic deposition of a 60 grid spacings thick layer onto the structure given in Figure 4.14. Due to the varying hole diameters, the voids form at different points of time leading to different thicknesses of the deposited layer within the cavities.
- 4.19. Isotropic etching of a “Swiss cheese“-structure with a constant etch rate of 1 grid spacing per time unit. (a) Initial geometry. (b)-(g) Illustration of the time evolution of the corresponding zero LS.
- 4.20. The parallel version of the H-RLE data structure given in Figure 3.7. An array of index vectors defines the grid segmentation. Each CPU processes the grid points of one segment in lexicographical order and writes the updated LS values into an own H-RLE data structure. For all other grid points which do not belong to the current CPU, run codes are inserted instead. They describe in which H-RLE data structure these points are stored.
- 5.1. If a particle trajectory intersects any tangential disk (thick black)
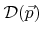 , it contributes to the rates of the corresponding active grid point (black)
, it contributes to the rates of the corresponding active grid point (black)
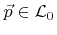 . Due to the curvature of the surface
. Due to the curvature of the surface
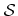 , the calculation of the particle trajectory must be continued for a few grid spacings in order to obtain correct rates. However, new reemitted particles (dashed) are always launched from the surface intersection point. To avoid multiple intersection tests of the same disk, only those grid points which are opposite to the entry face are checked, if they are active and if their corresponding disk is intersected. The numbers show which points are processed in which cell.
, the calculation of the particle trajectory must be continued for a few grid spacings in order to obtain correct rates. However, new reemitted particles (dashed) are always launched from the surface intersection point. To avoid multiple intersection tests of the same disk, only those grid points which are opposite to the entry face are checked, if they are active and if their corresponding disk is intersected. The numbers show which points are processed in which cell.
- 5.2. Additional particles are started from positions, which are offset by a multiple of the lateral domain extension, in order to account for the primary flux coming through the open domain boundaries.
- 5.3. The computational effort for calculating a particle trajectory can be reduced by using a subdivision of the simulation domain into boxes. Empty grid cells are combined in larger boxes while non-empty grid cells (gray) are boxes by their own. There are various splitting strategies to obtain a suitable decomposition.
- 5.4. The arrays
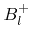 and
and 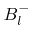 with
with
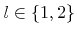 store the neighbor links of all subboxes for the positive and negative
store the neighbor links of all subboxes for the positive and negative 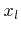 -direction, respectively. The array indices
-direction, respectively. The array indices
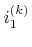 and
and
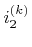 , which are stored together with box
, which are stored together with box
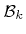 in array
in array 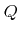 , give access to the corresponding links. The additional arrays
, give access to the corresponding links. The additional arrays 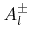 with
with
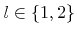 allow fast access from the outside.
allow fast access from the outside.
- 5.5. A deposition process simulation was used for the benchmarks.
- 5.6. The sum of the given direction
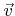 and a random unit vector
and a random unit vector
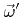 uniformly distributed over a sphere leads to a cosine distribution.
uniformly distributed over a sphere leads to a cosine distribution.
- 5.7. Flow chart of the simulation algorithm.
- 6.1. Two-dimensional simulations of a deposition process for various sticking coefficients
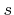 and reaction orders
and reaction orders 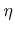 .
.
- 6.2. The initial geometry was resolved on a grid with lateral extensions
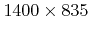 .
.
- 6.3. The profile after deposition of a 15 grid spacings thick layer.
- 6.4. The profile after deposition of a 30 grid spacings thick layer.
- 6.5. The final profiles after
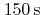 of etching in a SF
of etching in a SF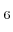 /O
/O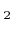 plasma for different gas compositions. The two level sets which are used to represent the two material regions, the mask and the substrate, are shown.
plasma for different gas compositions. The two level sets which are used to represent the two material regions, the mask and the substrate, are shown.
- 6.6. Plasma etching simulation for a three-dimensional structure. The same parameters are used as for the simulation presented in Figure 6.5c.
- 6.7. Anisotropic wet etching of a silicon substrate through a quadratic aperture. The lateral extensions of the simulation domain are
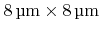 and the grid resolution is
and the grid resolution is
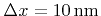 . The simulation boundaries are aligned to
. The simulation boundaries are aligned to
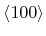 directions.
directions.
- 6.8. The LS representations at different times for an anisotropic wet etching process. The lateral domain boundaries are aligned to
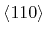 directions. The structure size is
directions. The structure size is
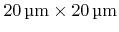 .
.
- 6.9. The final profiles after 20 cycles for different combinations of deposition/etching process times.
- 6.10. Deep reactive ion etching of holes with varying diameters (
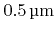 ,
,
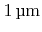 ,
,
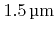 ,
,
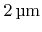 , and
, and
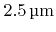 ). The lag effect is the reason for the different depths. The structure is resolved on a grid with lateral extensions
). The lag effect is the reason for the different depths. The structure is resolved on a grid with lateral extensions
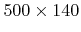 .
.
- 6.11. The characteristic dependence of the neutral and ion fluxes at the bottom center on the aspect ratio.
- 6.12. Ion beam milling of a step structure for an incident angle of
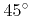 .
.
- 6.13. (a)-(g) Serpentine scan of
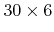 pixels with dwell time of
pixels with dwell time of
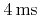 . (h) Four passes of a serpentine scan with dwell time of
. (h) Four passes of a serpentine scan with dwell time of
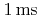 .
.
- A.1. The line defined by the point
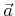 and the unit vector
and the unit vector
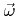 intersects the triangle given by
intersects the triangle given by
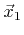 ,
,
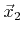 , and
, and
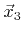 , if the signed areas
, if the signed areas 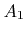 ,
, 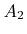 , and
, and 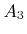 have the same sign. (a)
have the same sign. (a) 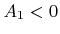 ,
, 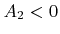 , and
, and 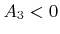 , which implies that the line intersects the triangle. (b) No intersection, since
, which implies that the line intersects the triangle. (b) No intersection, since 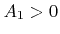 ,
, 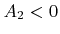 , and
, and 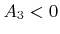 .
.



Next: List of Tables
Up: Dissertation Otmar Ertl
Previous: Contents
Otmar Ertl: Numerical Methods for Topography Simulation