1.2 Schematic of the device constructed by Lehovec. The PN junction in series works as a barrier to prevent the undesired current flow through the silicon. Image based on [10].
1.3 Description of the planar process developed by Jean Hoerni for a diode (left side) and a transistor (right side). A sample of an n-type Silicon substrate is prepared with silicon oxide on top (a and e). In predetermined regions the oxide is etched (b and f), opening spots for impurity diffusion (c, f, and g). After diffusion, an oxide layer is regrown in the etched openings and the metal contacts are deposited (d and h). Image based on [11].
1.4 Moore’s law in semi-log scale.
1.5 Different implementations of a 3D IC: Monolithic device (a), Die-to-die integration (b), and Wafer-to-wafer integration (c).
1.6 Typical processing of a TSV. A Die (or wafer) ready (a) for TSV manufacturing is polished (b) on its backside to reduce the thickness. In the following, the sample is structured by photolithography (c) and the via hole is etched (d). Then, the metal pad is exposed (e) and the conduction metal is deposited (f and g), accordingly to the TSV type. Finally, the die (or wafers) are stacked and bonded.
1.7 The three main approaches for TSV fabrication: Via First, Via Middle and Via Last. Image based on [32].
1.8 A conceptual example of 2.5D technology. The silicon interposer is used to reduce the connection paths between the chips.
2.1 Relationship between force and deformation. The linear region is known as the elastic regime and any deformation in this regime is temporary and ceases to exist after unloading. Beyond the elastic limit the deformations become permanent and the material enters the plastic regime.
2.2 General deformation of a body after external loading. Rigid body movements such as translation and rotation are included, although they should not count for the final body deformed state.
2.3 Geometrical representation of the normal and shear strain.
2.4 Complementary angles in the plane xy. The indicated angles on the bottom left corner of the quadrilateral are equal to those on the upper right corner, due to triangle symmetry.
2.5 Uniaxal load of a body. The stress is defined as the force divided by the area.
2.6 The dependence of stress on the chosen plane. A body under a load (a) can have different stress configurations at a point, depending on the considered plane (b and c). However, they must describe the same physical phenomenon.
2.7 Stress definition in a cube.
2.8 Visualization of the tensorial Hooke’s law. Strain symmetry forces symmetry on the
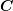 tensor
on all components in the form
tensor
on all components in the form 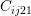 ,
, 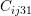 , and
, and 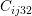 indicated by numbers
in gray. Strain symmetry is enforced on the components
indicated by numbers
in gray. Strain symmetry is enforced on the components 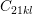 ,
, 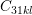 , and
, and
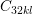 indicated by the brown squares.
indicated by the brown squares.2.9 Superposition of effects during an uniaxial loading of a body, where
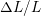 is the normal strain
is the normal strain 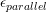 along
the direction of the applied force and
along
the direction of the applied force and 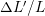 is the normal strain
is the normal strain 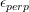 in the
directions perpendicular to the force.
in the
directions perpendicular to the force.2.10 Material plasticity in the stress-strain curve. Unloads in the work hardening region retain the deformation history and any subsequent load will relate linearly with the strain until the original unload point is reached (“New” Yield strength). Beyond the work hardening region the material enters a perfect plastic regime, where increases to the yield strength can be considered (most of the time) negligible.
2.11 Defect movement triggered by shear stress.
2.12 Von Mises versus Tresca criteria in a 2D system.
3.1 A set of linear basis functions of
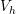 . As the number of partitions increases, the amount
of functions which are possible to represent the solution (
. As the number of partitions increases, the amount
of functions which are possible to represent the solution (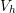 dimension) also
increases. As consequence, the quality of the approximation is enhanced.
dimension) also
increases. As consequence, the quality of the approximation is enhanced.3.2 Linear basis function constructed according to the presented criteria.
3.3 An example of a piecewise linear polynomial function. For each partition a linear function is defined.
3.4 Quadratic (left) and cubic (right) basis function.
3.5 Basis functions defined in 2D domains. Linear (a) and quadratic (b) functions in quadrilateral domains.
3.6 Geometrical interpretation of Galerkin’s method. The solution (
 ) of the original problem is projected (
) of the original problem is projected (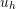 ) in the space defined by the basis
of
) in the space defined by the basis
of 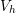 . Galerkin’s method can be understood as the procedure to find this
projection.
. Galerkin’s method can be understood as the procedure to find this
projection.3.7 Inifinitesimally small stress cube. The stress is defined in the face of the cube, however only
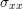 is explicitly shown. The others are omitted
for the sake of clarity in the picture.
is explicitly shown. The others are omitted
for the sake of clarity in the picture.3.8 General elastic problem. B is the body force and g an external load. The surface
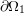 is free to move, while
is free to move, while 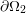 is
constrained.
is
constrained.3.9 Partioning of the domain in time steps. The solution is computed at each time step.
4.1 Schematic of the standard TSVs considered in this work for unfilled (a) and filled (b) technology. The vias have a 100
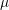 m diameter and
250
m diameter and
250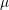 m height. Filled TSVs are usually smaller than the one presented here,
however, the dimensions were chosen in order to allow for a fair comparison
between both technologies.
m height. Filled TSVs are usually smaller than the one presented here,
however, the dimensions were chosen in order to allow for a fair comparison
between both technologies.4.2 Von Mises stress in the unfilled TSV. As depicted in the inset the top corner of the via is a point of high stress, especially in the oxide. Naturally, the metal sustains the highest stress in the structure. However, oxides are usually not as resistant to mechanical stress as copper or tungsten. The scale is normalized to the maximum stress obtained for this setup.
4.3 Von Mises stress in the filled TSV. The stress pattern is similar to the unfilled TSV (including the high stress spot at the top). However, the overall stress in the silicon is higher than the stress in the unfilled TSV. The scale is normalized to the maximum stress obtained for this setup.
4.4 Stress fields in the unfilled TSV (left) and filled TSV (right). Cylindrical coordinates are used to simplify the analysis.
4.5 Von Mises stress through the silicon layer along the radial direction through the middle of the TSV height. For the unfilled TSV the choice of material is negligible for the stress level in the silicon. Most of the stress is produced by the geometry itself. In the filled TSV the metal plays a significant role. A large difference between the CTE of silicon and the metal creates high levels of stress, as shown by the Cu filled TSV.
4.6 Problem description of the stress created by unfilled TSVs due to thermal expansion.
4.7 Solution of the different materials. The solution form is kept, since the equilibrium equation must be satisfied in every material. The constants are solely determined by the material parameters and via geometry. They can be computed by imposing boundary conditions and interface conditions (continuous displacement and radial stress between the interfaces).
4.8 Comparison between the FEM solution and the analytical solution described in this section.
4.9 A particular arrangement of 7 TSVs. The vias are equidistant (300
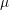 m) from each other.
m) from each other.4.10 Von Mises stress of the 7 TSVs pattern. The stress superposition between the TSVs creates stress-free spots. The TSVs’ placement can be chosen to minimize the stress impact in silicon.
4.11 Von Mises stress between two TSVs. The characteristic stress curve of each TSV is superimposed to its neighbor, creating this particular pattern.
4.12 Comparison between the stress along the radial direction at the top and bottom of the TSV with the stress in the middle (analytical solution). For points close to the TSV edges, the analytical solution provides a fair approximation. For points further from the TSV edge (20um), it can still be used as a lower bound estimate for the stress.
5.1 A TSV (left) and a full-plate (right) sample during X-Ray measurements. The TSV geometry hinders the X-Ray reach, while a full-plate sample with the same layer profile is used to evaluate the stress in the metal.
5.2 Two-dimensional cross section of the TSV. The Bosch scallops are shown in detail.
5.3 Schematic of the single (a) and double (b) stack structures considered for the simulation.
5.4 Comparison between the Bézier curve description of the scallops to the Bosch process simulation (a) and the fabricated scallop (b). Bézier curves create sharp points between the scallops, which could lead to unrealistic stress build-up at these meeting points during simulation.
5.5 Scallop shape approximation by two Bézier curves. The curvature, height, and width are controlled by the weights.
5.6 Mesh details around the scallops for the single (a) and double (b) stack structure.
5.7 Stress distribution along the TSV in the vertical (top) and tangential direction (bottom) considering vias with weak adhesion (left), no weak adhession (middle) and without scallops (right). The stress is strongly reduced in the vertical direction, mainly due to the scalloped geometry. The weak adhesion induces a small reduction, but it is not the main mechanism. Along the tangential direction, the scalloped geometry is not so evident, hence the stress reduction is very small.
5.8 The same behavior for the stress is found in double stack structures. However, the reduction due to the scalloped sidewall is slightly smaller when compared to single stack TSVs.
5.9 Displacement in the radial direction. The scallop creates points which ease the movement of the metal, relaxing the overall stress in the metal layer.
5.10 Points of high stress in the scallops. Although there is an overall reduction of the stress in the metal layers, the scallops create points of stress accumulation, which can easily surpass the average layer stress.
5.11 Maximum von Mises stress variation dependence on the height and width of the TSV sidewall scallops.
5.12 Wafer bow due to film deposition. The curvature depends if the film stress is tensile (positive) or compressive (negative).
5.13 A wafer forced to unbow during handling or processing.
5.14 Schematic of the multilevel approach for a simulation of large scale effects in the TSV.
5.15 Result of the last simulation level of a multilevel simulation of a filled TSV. The material inside the cavity provides better support against forces at the bottom of the TSV.
5.16 Simulation of the effects of a forced unbow on the TSV. In the first level, no TSV is considered. For the second level the vias are treated as regular holes in the silicon. Only at the last level the TSV is considered in full detail. The unbow movement is particularly dangerous for the bottom and top corners of the via.
5.17 Dislocation propagation inside a film crystal.
5.18 Slip system inside a material. A force parallel to the slip plane must exist in order to activate the dislocations movement.
5.19 Comparison between experimental data, FEM coupling, and GA fitting result.
5.20 Stress evolution at the TSV top for the metal layer. The stress in the vertical direction sustains an elastic behavior, because the stress level along the thermal cycle is not sufficient to activate the glide mechanism.
5.21 Stress evolution at the TSV middle for the metal layer. The von Mises stress increases during heating and could damage the structure.
6.1 Typical steps during the growth of a thin film. The material is transported towards the substrate (a), where it deposits. The adatoms diffuse (b) over the surface, moving towards low energy sites. As more adatoms arrive, agglomerates begin to form (c) and the first islands nucleate (d). The new arrived adatoms are incorporated into the islands (e), which grow until they reach each other and coalesce, forming the grain boundaries (f).
6.2 The three modes of film growth: Frank-van der Merwe (a), Volmer-Weber (b), and Stransky-Karastanov (c).
6.3 Metal film growth process. The final film structure depends on the adatom mobility of the depositing metal.
6.4 Stress behavior during the film growth process.
6.5 Hoffman model.
6.6 Nix-clemens model.
6.7 Freund-chason model.
6.8 Structure considered for coalescence simulations. The droplets come in contact at a height
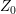 and the surface is displaced at most by
and the surface is displaced at most by 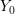 . The
angle formed between the droplet and the deposition substrate is identified
by
. The
angle formed between the droplet and the deposition substrate is identified
by 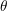 . Image based on [98].
. Image based on [98].6.9 Snapshot of the VW simulation used in this section. The grains will grow until the entire substrate is covered.
6.10 Droplet size distribution during coalescence for the growth parameters considered in this work. The droplets’ sizes follow an exponential distribution.
6.11 FEM simulation of a single encounter between two droplets. Symmetry conditions are employed from both sides. A prescribed displacement is applied at the surface of both grains up to a critical height
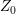 .
.6.12 Method to estimate the average residual stress.
6.13 Residual stress estimation. The simulated results follow a normal distribution. The mean is the residual stress estimate and the distribution spreading is the expected deviation from the estimate.